JEE Advanced (Fill in the Blanks): Applications of Derivatives | Chapter-wise Tests for JEE Main & Advanced PDF Download

Fill in the Blanks

Q.1. The larger of cos (ln θ) and ln (cos θ) if 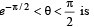 ..........        (1983 - 1 Mark)

Ans. cos(ln θ)

Solution.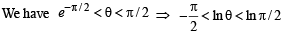 

⇒ cos (–π/2) < cos (ln θ) < cos (ln π/2)
⇒ cos (ln θ) > 0 ....... (1)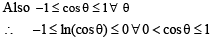

⇒ ln (cos q) < 0 ....... (2)
From (1) and (2) we get, cos (ln θ) > ln (cos θ)
∴ cos (ln θ) is larger.

Q.2. The function y = 2x²- ln |x| is monotonically increasing for values of x(≠ 0) satisfying the inequalities ....... and monotonically decreasing for values of x satisfying the inequalities ..................          (1983 - 2 Marks)

Ans.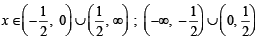 

Solution.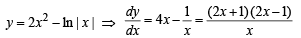 

Critical points are 0, 1/2, –1/2

Clearly f (x) is increasing on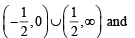 

f (x) is decreasing on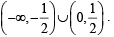 

Q.3. The set of all x for which ln(1 + x) < x is equal to ...............           (1987 - 2 Marks)

Ans. x > 0

Solution. Let f (x) = log (1 + x) – x  for x > – 1

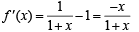
We observe that,

f ' (x) >0 if – 1 < x < 0 and f '(x) <0 if x > 0

Therefore f increases in (– 1, 0) and decreases in (0, ∞).

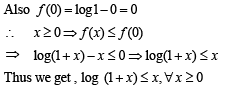
Q.4. Let P be a variable point on the ellipse 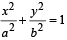with foci F₁ and F₂ . If A is the area of the triangle PF₁F₂ then the maximum value of A is ..............       (1994 -  2 Marks)

Ans. abe

Solution. Let P(a cos θ,b sinθ) be any point on the ellipse 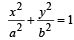  with foci F₁ (ae, 0) and F₂ (–ae, 0)

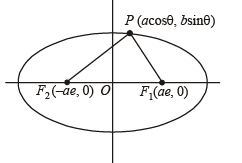
Then area of DPF₁F₂ is given by

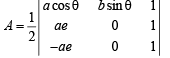
∵ | sin θ | < 1
∴ A_max = abe

Q.5. Let C be the curve y³ – 3xy + 2 = 0. If H is the set of points on the curve C where the tangent is horizontal and V is the set of the point on the curve C where the tangent is vertical then H =............ and V = .............            (1994 -  2 Marks)

Ans. φ, {(1, 1)}

Solution. The given curve is C : y³ – 3xy + 2 = 0

Differentiating it with respect to x, we get

∴ Slope of tangent to C at point (x₁, y₁) is

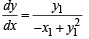
For horizontal tangent, dy/dx = 0 ⇒ y₁ = 0

For y₁ = 0 in C, we get no value of x₁
∴ There is no point on C at which tangent is horizontal

∴ H = φ

For vertical tangent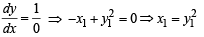 

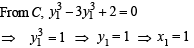
∴ There is only one point (1, 1) at which vertical tangent can be drawn

∴ V = {(1, 1)}

True / False

Q. 1. If x – r is a factor of the polynomial f (x) = a_nx⁴ + .... + a₀ , repeated m times (1 < m < n), then r is a root of f '(x) = 0 repeated m times.       (1983 - 1 Mark)

Ans. F

Solution. If (x – r) is a factor of f (x) repeated m times then f ' (x) is a polynomial with (x – r) as factor repeated (m – 1) times.

∴ Statement is false.

Q. 2. For 0 < a < x,  th e minimum value of the function log_a x + log_xa is 2.       (1984 - 1 Mark)

Ans. F

Solution. Given that 0 < a < x.

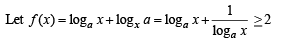
But equality holds for log_a x = 1

⇒ x = a which is not possible.

∴ f (x) > 2

∴ f_min cannot be 2.

∴ Statement is false.