JEE Advanced (Fill in the Blanks): Circle | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. If A and B are points in the plane such that PA/PB = k (constant) for all P on a given circle, then the value of k cannot be equal to ..................... (1982 - 2 Marks)
Ans. 1
Sol. As P lies on a circle and A and B two points in the plane
such that 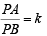
Then k can be any real number except 1 as otherwise P will lie on perpendicular bisector of AB which is a line.
Q.2. The points of intersection of the line 4x – 3y – 10 = 0 and the circle x2 + y2 – 2x + 4y – 20 = 0 are .................... and ..................... (1983 - 2 Marks)
Ans. (4, 2), (–2, –6)
Sol. For point of intersection of line 4x – 3y – 10 = 0 … (1)
and circle x2 + y2 – 2x + 4y – 20 = 0 … (2)
Solving (1) and (2), we get
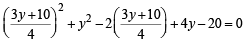
⇒ y2 + 4y – 12 = 0 ⇒ y = 2, – 6
⇒ x = 4,– 2
∴ Points are (4, 2) and (– 2, – 6)
Q.3. The lines 3x – 4y + 4 = 0 and 6x – 8y – 7 = 0 are tangents to the same circle. The radius of this circle is ..................... (1984 - 2 Marks)
Ans. 3/4
Sol. Let 3x – 4y + 4 = 0 be the tangent at point A and 6x – 8y – 7 = 0 be the tangent of point B of the circle.
As the two tangents parallel to each other
∴ AB should be the diameter of circle.
∴ AB = distance between parallel lines
3x – 4y + 4 = 0 and
6x – 8y – 7 = 0 = distance between
6x – 8y + 8 = 0 and 6x – 8y – 7 = 0
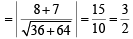
∴ radius of circle = 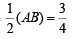
Q.4. Let x2 + y2 – 4x – 2y – 11 = 0 be a circle. A pair of tangents from the point (4, 5) with a pair of radii form a quadrilateral of area ..................... (1985 - 2 Marks)
Ans. 8 sq. units
Sol. KEY CONCEPT :
Length of tangent from a point (x1, y1) to a circle x2 + y2 + 2gx + 2fy + c = 0 is given by
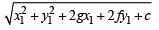
The equation of circle is, x2 + y2 – 4x – 2y – 11 = 0
It's centre is (2, 1), radius =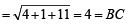
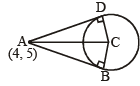
length of tangent from the pt. (4, 5) is
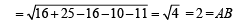
∴ Area of quad. ABCD
= 2 (Area of ΔABC) 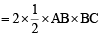
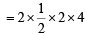 = 8 sq. units.
= 8 sq. units.
Q.5. From the origin chords are drawn to the circle (x – 1)2 + y2 = 1. The equation of the locus of the mid-points of these chords is ..................... (1985 - 2 Marks)
Ans. x2 + y2 – x = 0
Sol. The equation of given circle is (x – 1)2 + y2 = 1
or x2 + y2 – 2x = 0 … (1)
KEY CONCEPT : We know that equation of chord of curve S = 0, whose mid point is (x1, y1) is given by T = S1 where T is tangent to curve S = 0 at (x1, y1).
∴ If (x1, y1) is the mid point of chord of given circle (1), then equation of chord is
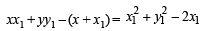
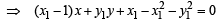
At it passes through origin, we get
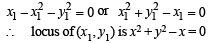
Q.6. The equation of the line passing through the points of intersection of the circles 3x2 + 3y2 – 2x + 12y – 9 = 0 and x2 + y2 + 6x + 2y – 15 = 0 is ..................... (1986 - 2 Marks)
Ans. 10x – 3y – 18 = 0
Sol. The equation of two circles are
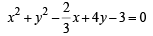 … (1)
… (1)
and x2 + y2 + 6x + 2y – 15 = 0 … (2)
Now we know eq. of common chord of two circles
S1 = 0 and S2 = 0 is S1 – S2 = 0
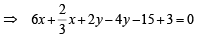
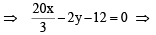 10x – 3y – 18 = 0
10x – 3y – 18 = 0
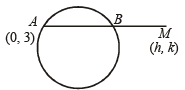
Q.7. From the point A(0, 3) on the circle x2 + 4x + (y – 3)2 = 0, a chord AB is drawn and extended to a point M such that AM = 2AB. The equation of the locus of M is .................. (1986 - 2 Marks)
Ans.
Sol. The equation of circle is, x2 + y2 + 4x – 6y + 9 = 0 … (1)
AM = 2AB
⇒ AB = BM
Let the co-ordinates of M be (h, k) Then B is mid pt of AM
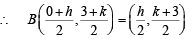
As B lies on circle (1),
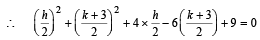
⇒ h2 + k2 + 8h – 6k + 9 = 0
∴ locus of (h, k) is, x2 + y2 + 8x – 6y + 9 = 0
Q.8. The area of the triangle formed by the tangents from the point (4, 3) to the the circle x2 + y2 = 9 and the line joining their points of contact is ..................... (1987 - 2 Marks)
Ans. 192/25
Sol. From P (4, 3) two tangents PT and PT' are drawn to the circle x2 + y2 = 9 with O (0, 0) as centre and r = 3.
To find the area of ΔPTT'.
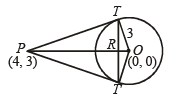
Let R be the point of intersection of OP and TT'.
Then we can prove by simple geometry that OP is perpendicular bisector of TT'.
Equation of chord of contact TT' is 4x + 3y = 9 Now, OR = length of the perpendicular from O to TT' is
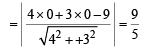
OT = radius of circle = 3
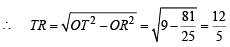
Again OP = 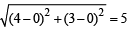
∴ PR = OP - OR = 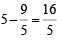
Area of the triangle
PTT' = PR x TR 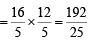
Q.9. If the circle C1 : x2 + y2 = 16 intersects anoth er circle C2 of radius 5 in such a manner that common chord is of maximum length and has a slope equal to 3/4, then the coordinates of the centre of C2 are ..................... (1988 - 2 Marks)
Ans.
Sol. We have C1 : x2 + y2 = 16, Centre O1 (0, 0) radius = 4. C2 is another circle with radius 5, let its centre O2 be (h, k).
Now the common chord of circles C1 and C2 is of maximum length when chord is diameter of smaller circle C1, and then it passes through centre O1 of circle C1. Given that slope of this chord is 3/4.
∴ Equation of AB is,
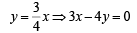 … (1)
… (1)
In right ΔAO1O2,
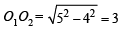
Also 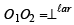 distance from (h, k) to (1)
distance from (h, k) to (1)
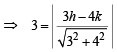
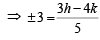
⇒ 3h – 4k ± 15 = 0 … (2)
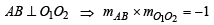
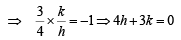 … (3)
… (3)
Solving, 3h – 4k + 15 = 0 and 4h + 3k = 0
We get h = – 9/5, k = 12/5
Again solving 3h – 4k – 15 = 0 and 4h + 3k = 0
We get h = 9/5, k = –12/5
Thus the required centre is 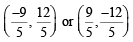
Q.10. The area of the triangle formed by the positive x-axis and the normal and the tangent to the circle x2 + y2 = 4 at 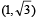 is, ..................... (1989 - 2 Marks)
is, ..................... (1989 - 2 Marks)
Ans.
Sol. Tangent at P (1, 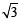 ) to the circle x2 + y2 = 4 is x . 1 + y .
) to the circle x2 + y2 = 4 is x . 1 + y .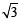 = 4
= 4
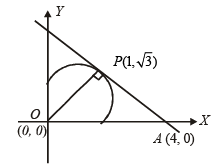
It meets x-axis at A (4, 0),
∴ OA = 4 Also OP = radius of circle = 2 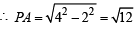
∴ Area of ΔOPA =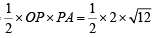
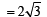 sq. units
sq. units
Q.11. If a circle passes through the points of intersection of the coordinate axes with the lines λx – y + 1 = 0 and x – 2y + 3 = 0, then the value of λ = ................... (1991 - 2 Marks)
Ans. 2
Sol. The given lines are lx – y + 1 = 0 and x – 2y + 3 = 0 which meet x-axis at 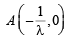 and B (– 3, 0) and
and B (– 3, 0) and
y-axis at C (0, 1) and D 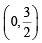 respectively..
respectively..
Then we must have, OA × OB = OC × OD
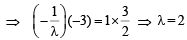
Q.12. The equation of the locus of the mid-points of the circle 4x2 + 4y2 – 12x + 4y + 1 = 0 that subtend an angle of 2π/ 3 at its centre is ..................... (1993 - 2 Marks)
Ans. 16x2 + 16y2 – 48x + 16y + 31 = 0
Sol. The given circle is, 4x2 + 4y2 – 12x + 4y + 1 = 0
or 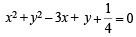 with centre
with centre 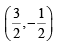
and 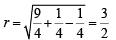
Let M (h, k) be the mid pt. of the chord AB of the given circle, then CM ⊥ AB. ∠ ACB = 120°.
In ΔACM,
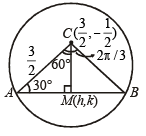
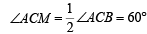
and ∠A = 30°
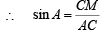
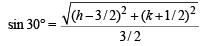
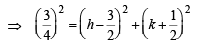
⇒ 16h2 + 16k2 – 48h + 16k + 31 = 0
∴ locus of (h, k) is 16x2 + 16y2 – 48x + 16y + 31 = 0
Q.13. The intercept on the line y = x by the circle x2 + y2 – 2x = 0 is AB. Equation of the circle with AB as a diameter is ..................... (1996 - 1 Mark)
Ans. x2 + y2 – x – y = 0
Sol. Equation of any circle passin g through the point of intersection of x2 + y2 – 2x = 0 and y
= x is x2 + y2 – 2x + l (y – x) = 0
or x2 + y2 – (2 + l)x + ly = 0
Its centre is 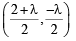
For AB to be the diameter of the required circle, the centre must lie on AB. That is,
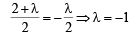
Thus, equation of required circle is x2 + y2 – 2x – y + x = 0 or x2 + y2 – x – y = 0
Q.14. For each natural number k, let Ck denote the circle with radius k centimetres and centre at the origin. On the circle Ck, a-particle moves k centimetres in the counter-clockwise direction. After completing its motion on Ck, the particle moves to Ck+1 in the radial direction. The motion of the particle continues in this manner. The particle starts at (1, 0).
If the particle crosses the positive direction of the x-axis for the first time on the circle Cn then n = ..................... (1997 - 2 Marks)
Ans. 7
Sol.
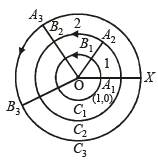
The radius of circle C1 is 1 cm, C2 is 2 cm and soon.
It starts from A1 (1, 0) on C1, moves a distance of 1 cm on C1 to come to B1. The angle subtended by A1B1 at the centre
will be 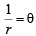 radians, i.e. 1 radian.
radians, i.e. 1 radian.
From B1 it moves along radius, OB1 and comes to A2 on circle C2 of radius 2. From A2 it moves on C2 a distance 2 cm and comes to B2. The angle subtended by A2B2 is again as before 1 radian. The total angle subtended at the centre is 2 radians. The process continues. In order to cross the x-axis again it must describe 2p radians i.e 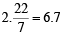 radians.
radians.
Hence it must be moving on circle C7
∴ n = 7
Q.15. The chords of contact of the pair of tangents drawn from each point on the line 2x+y =4 to circle x2+y2 = 1 pass through the point ..................... (1997 - 2 Marks)
Ans.
Sol. Let (h, k) be any point on the given line
∴ 2h + k = 4 and chord of contact is hx + ky = 1 or hx + (4 – 2h) y = 1
or (4y – 1) + h (x – 2y) = 0
P + l Q = 0.It passes through the intersection of P = 0 and
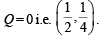
|
446 docs|930 tests
|






















