JEE Advanced (Fill in the Blanks): Complex Numbers | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q. 1. If the expression (1987 - 2 Marks)
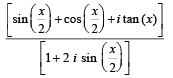
is real, then the set of all possible values of x is ............
Ans. 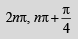
Sol.
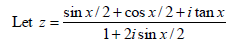
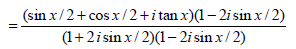
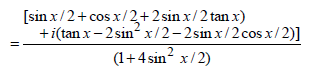
But ATQ, Im(z) = 0 (as z is real)


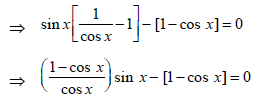
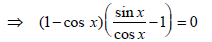
⇒ cos x = 1 ⇒ x = 2nπ and
tan x = 1 ⇒ x= nπ + π/4
∴ x = 2nπ, nπ + π/4
Q. 2. For any two complex numbers z1, z2 and any real number a and b. (1988 - 2 Marks) | az1 – bz2 |2 + | bz1 + az2 |2 = .............
Ans. (a2 + b2 )(| z1 |2+ |z2 |2)
Sol.
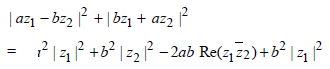
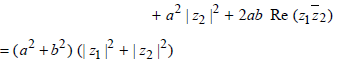
Q. 3. If a, b, c, are the numbers between 0 and 1 such that the points z1 = a + i, z2 = 1 + bi and z3 = 0 form an equilateral triangle, then a = .......and b = ........... (1989 - 2 Marks)
Ans. 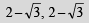
KEY CONCEPT : | z1 - z2 |= distance between two points represented by z1 and z2.
As z1 = a + i, z2 = 1+ bi and z3 = 0 form an equilateral triangle, therefore
|z1 – z3| = |z2 – z3| = |z1 – z2|
| a + i | = | 1+ bi | = | ( a – 1) + i (1– b) |
⇒ a2 + 1= 1+ b2 = (a – 1)2 + (1– b)2
⇒ a2 = b2 = a2 + b2 – 2a – 2b + 1
⇒ a = b ....(1)
(∴ a, b > 0 ∴ a≠ – b ) and
b2 – 2a – 2b + 1= 0
or a2 – 2a – 2b + 1 = 0 ....(2)
⇒ a2 – 2a – 2a + 1= 0 [∴a = b]
⇒ a2 – 4a + 1 = 0

Q. 4. ABCD is a rhombus. Its diagonals AC and BD intersect at the point M and satisfy BD = 2AC. If the points D and M represent the complex numbers 1 + i and 2 - i respectively, then A represents the complex number .........or.......... (1993 - 2 Marks)
Ans. 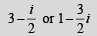
Sol :
If we see the problem as in co-ordinate geometry we have D ≡ (1,1) and M≡ (2, – 1)
We know that diagonals of rhombus bisect each other at 90°
∴ AC passes through M and is ^ to BD
∴ Eq. of AC in symmetric form can be written as

Now for pt. A, as



Q. 5. Suppose Z1, Z2, Z3 are the vertices of an equilateral triangle inscribed in the circle |Z| = 2. If Z1 = 1 + 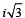 then Z2 = ........, Z3 = ............ (1994 - 2 Marks)
then Z2 = ........, Z3 = ............ (1994 - 2 Marks)
Ans. –2, 1 - 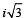
Sol :
Let z1, z2,z3 be the vertices A, B and C respectively of equilateral ΔABC, inscribed in a circle | z | = 2, centre (0, 0) rasius = 2




Q. 6. The value of the expression

where w is an imaginary cube root of unity, is..... (1996 - 2 Marks)
Ans. 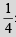 n (n - 1)(n2 + 3n + 4)
n (n - 1)(n2 + 3n + 4)
Sol:
rth term of the given series,
= r [(r +1) –ω](r +1) –w2 ]
= r [(r +1)2 – (ω+ω2 )(r +1) +ω3]
= r [(r +1)2 – (-1)(r +1) +1]
= r [(r2 + 3r + 3] = r3 + 3r2 + 3r
Thus, sum of the given series,



|
446 docs|930 tests
|






















