JEE Advanced (Fill in the Blanks): Limits, Continuity & Differentiability | Chapter-wise Tests for JEE Main & Advanced PDF Download
Fill in the Blanks
Q. 1. 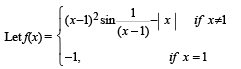
be a real-valued function. Then the set of points where f(x) is not differentiable is .......................
Ans. 0
Solution.
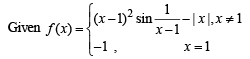
We know that | x | is not differentiable at x = 0
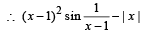 is not differentiable at x = 0.
is not differentiable at x = 0.
At all other values of x, f(x) is differentiable.
∴ The req. set of points is {0}.
Q. 2. 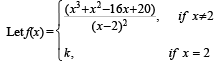
If f(x) is continuous for all x, then k = ..........
Ans. k = 7
Solution. It will be continuous at x = 2 if
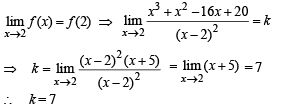
Q. 3. A discontinuous function y =f(x) satisfying x2 +y2 = 4 is given by f(x) = .......................
Ans.
Solution. 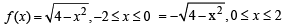
By choosing any arcs of circle x2 – y2 = 4, we can define a discontinuous function, one of which is
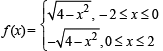
Q. 4. 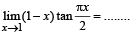
Ans. 2/π
Solution. KEY CONCEPT
(L' Hospital rule)
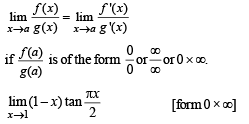
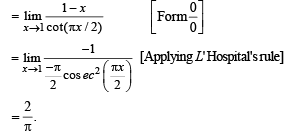
Q. 5. If f(x) = sin x, x ≠ np,n = 0, ± 1, ± 2,± 3, .............. = 2, otherwise
and g(x) = x2 + 1,x ≠ 0,2
= 4, x = 0
= 5, x = 2,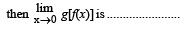
Ans. 1
Solution. Given that,
f (x) = sin x, x ≠ p,n = 0, ±1,± 2,... = 2, otherwise
And g(x) = x2 + 1, x ≠ 0,2
= 4, x = 0 = 5, x = 2
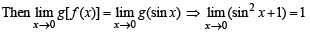
Q. 6. 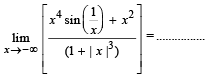
Ans. -1
Solution.
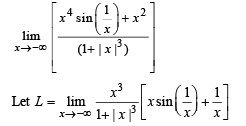
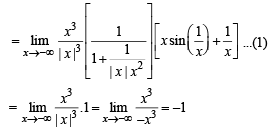
Q. 7. 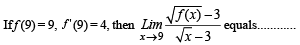
Ans. 4
Solution.
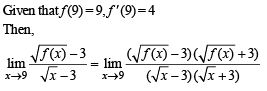
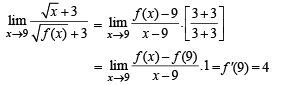
Q. 8. ABC is an isosceles triangle inscribed in a circle of radius r. If AB = AC and h is the altitude from A to BC then the triangle ABC has perimeter 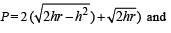
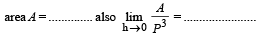
Ans. 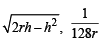
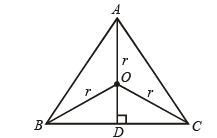
Solution. In Δ ABC, AB = AC
AD ⊥ BC (D is mid pt of BC)
Let r = radius of circumcircle
∴ OA = OB = OC = r
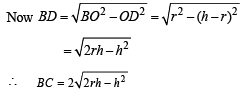
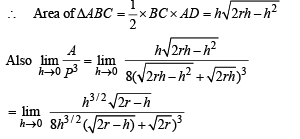
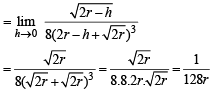
Q. 9. 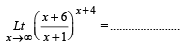
Ans. e5
Solution.
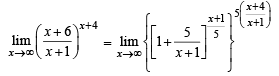
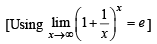
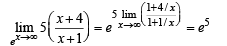
Q. 10. Let f(x) = x | x |. The set of poin ts wh ere f(x) is twice differentiable is .....................
Ans. R – {0}
Solution. We have,
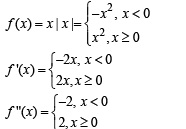
Clearly f " (x) exists at every pt. except at x = 0
Thus f (x) is twice differentiable on R – {0}.
Q. 11. 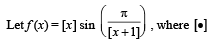 denotes the greatest integer function. The domain of f is... and the points of discontinuity of f in the domain are.....
denotes the greatest integer function. The domain of f is... and the points of discontinuity of f in the domain are.....
Ans. (-∞, - 1) ∪ [0, ∞), I – {0} where I is the set of ingeger except n = –1
Solution. Thus function is not defined for those values of x for which [x + 1] = 0.
In other words it means that
0 < x + 1 < 1 or – 1 < x < 0 .......(1)
Hence the function is defined outside the region given by (1).
Required domain is ] - ∞, -1[∪[0,∞] Now, consider integral values of x say x = n
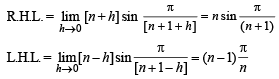
Clearly RHL ≠ LHL. Hence the given function is not continuous for integral values of n (n ≠ 0, –1).
At x = 0, f (0) = 0,
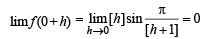
The function is not defined for x < 0. Hence we cannot find lim f (0 – h). Thus f (x) is continuous at x = 0. Hence the points of discontinuity are given by I – {0} where I is set of integers n except n = –1
Q. 12. 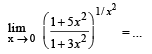
Ans. e2
Solution. KEY CONCEPT
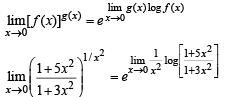
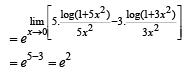
Q. 13. Let f(x) be a continuous function defined for 1 < x < 3. If f(x) takes rational values for all x and f (2) = 10, then f(1.5) =.............
Ans. 10
Solution. Since f (x) is given continuous on the closed bounded interval [1, 3], f (x) is bounded and assumes all the values lying in the interval [m, M] where
m = min f (x) and M = max f (x)
1 < x < 3 ⇒ f (1) < f (x) < (3)
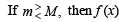 must assume all the irrational values lying in the [m, M]. But since f (x) takes only rational values, we must have m = M i.e., f (x) must be a constant function.
must assume all the irrational values lying in the [m, M]. But since f (x) takes only rational values, we must have m = M i.e., f (x) must be a constant function.
As f (2) = 10, we get
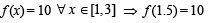
True / False
Q. 1. 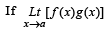 exists then both
exists then both 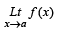 and
and 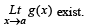
Ans. F
Solution.
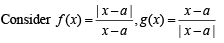
then 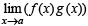 exists but neither
exists but neither 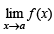
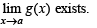
|
446 docs|929 tests
|
















