JEE Exam > JEE Notes > Chapter-wise Tests for JEE Main & Advanced > JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem
JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. The larger of 9950 + 10050 and 10150 is ................ (1982 - 2 Marks)
Ans. (101)50
Sol. Consider (101)50 – {(99)50 + (100)50} = (100 + 1)50 – (100 – 1)50 – (100)50
= (100)50 [(1+ 0.0 1)50 – (1– 0.01)50 – 1]
= (100)50 [2 (50C1(0.01) + 50C3(0.01)3 + ....) – 1]
= (100)50 [2 (50C3(0.01)3 + ....)] > 0
∴ (101)50 > (99)50 + (100)50
∴ (101)50 is greater.
Q.2. The sum of the coefficients of the plynomial (1 + x – 3x2)2163 is ................ (1982 - 2 Marks)
Ans. -1
Sol. If we put x = 1 in the expansion of (1+ x – 3x2)2163 = A0 + A1x + A2x2 + ...
we will get the sum of coefficients of given polynomial, which clearly comes to be – 1.
Q.3. If (1 + ax )n = 1 + 8x + 24x2 + .... then a = ...... and n = ............... (1983 - 2 Marks)
Ans. a = 2, n = 4
Sol. (1 + ax)n = 1 + 8x + 24x2 + ...
⇒ (1 + ax)n = 1 + nxa +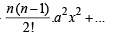
= 1 + 8 x + 24x 2+ ...
Comparing like powers of x we get
nax = 8x ⇒ na = 8 ....(1)
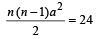
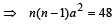....(2)
Solving (1) and (2), n = 4, a = 2
Q.4. Let n be positive integer. If the coefficients of 2nd, 3rd, and 4th terms in the expansion of (1 + x)n are in A.P., then the value of n is .............. (1994 - 2 Marks)
Ans. 7
Sol. We know that for a +ve integer n (1 + x)n = nC0 + nC1 x + nC2 x2 + ......+ nCn xn
ATQ coefficients of 2nd, 3nd, and 4th terms are in A.P. i.e.nC1, nC2, nC3 are in A.P.
⇒ 2.nC2 = nC1 + nC3
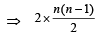
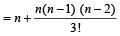
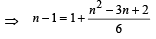⇒ n2 – 9n + 14 = 0
⇒ (n – 7) (n – 2) = 0 ⇒ n = 7 or 2
But for the existance of 4th term, n = 7.
Q.5. The sum of the rational terms in th e expansion of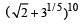 
is ................ (1997 - 2 Marks)
Ans. 41
Sol. Let Tr +1 be the general term in the expansion of
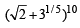
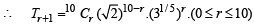
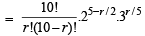
Let Tr +1will be rational if 25–r/2 and 3r/5 are rational numbers.
⇒ 
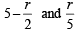are integers.
⇒ r = 0 and r = 10 ⇒ T1 and T11 are rational terms.
⇒ Sum of T1 and T11 = 10C025 – 0.30 + 10C1025–5.32
= 1.32.1 + 1.1.9 = 32 + 9 = 41
The document JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem | Chapter-wise Tests for JEE Main & Advanced is a part of the JEE Course Chapter-wise Tests for JEE Main & Advanced.
All you need of JEE at this link: JEE
|
446 docs|930 tests
|
Related Exams
About this Document
4.95/5
Rating
Apr 01, 2025
Last updated
Document Description: JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem for JEE 2025 is part of Chapter-wise Tests for JEE Main & Advanced preparation.
The notes and questions for JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem have been prepared according to the JEE exam syllabus. Information about JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem covers topics
like and JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem Example, for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem.
Introduction of JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem in English is available as part of our Chapter-wise Tests for JEE Main & Advanced
for JEE & JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem in Hindi for Chapter-wise Tests for JEE Main & Advanced course.
Download more important topics related with notes, lectures and mock test series for JEE
Exam by signing up for free. JEE: JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem | Chapter-wise Tests for JEE Main & Advanced
Description
Full syllabus notes, lecture & questions for JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem | Chapter-wise Tests for JEE Main & Advanced - JEE | Plus excerises question with solution to help you revise complete syllabus for Chapter-wise Tests for JEE Main & Advanced | Best notes, free PDF download
Information about JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem
In this doc you can find the meaning of JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem defined & explained in the simplest way possible. Besides explaining types of
JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem theory, EduRev gives you an ample number of questions to practice JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem tests, examples and also practice JEE
tests
Related Searches
MCQs
,study material
,Summary
,video lectures
,Semester Notes
,shortcuts and tricks
,Important questions
,Objective type Questions
,Sample Paper
,Previous Year Questions with Solutions
,JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem | Chapter-wise Tests for JEE Main & Advanced
,Extra Questions
,Exam
,practice quizzes
,ppt
,mock tests for examination
,Free
,JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem | Chapter-wise Tests for JEE Main & Advanced
,JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem | Chapter-wise Tests for JEE Main & Advanced
,Viva Questions
,past year papers
;
Additional Information about JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem for JEE Preparation
JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem Free PDF Download
The JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem is an invaluable resource that delves deep into the core of the JEE exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem now and kickstart your journey towards success in the JEE exam.
Importance of JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem
The importance of JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem cannot be overstated, especially for JEE aspirants.
This document holds the key to success in the JEE exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem Notes
JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem Notes on EduRev are your ultimate resource for success.
JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem JEE Questions
The "JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem JEE Questions" guide is a valuable resource for all aspiring students preparing for the
JEE exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem on the App
Students of JEE can study JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of JEE Advanced (Fill in the Blanks): Mathematical Induction & Binomial Theorem is prepared as per the latest JEE syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily