JEE Advanced (Fill in the Blanks & True/False): Gravitation | Chapter-wise Tests for JEE Main & Advanced PDF Download

Fill in the Blanks

Q.1. The numerical value  of the angular velocity of rotation of the earth should be ............rad/s in order to make the effective acceleration due to gravity equal to zero.  (1984 - 2 Marks)

Ans. 1.23 × 10^–3 rad/s

Solution. We know that g' = g – Rω² cos² φ 

At equator, φ = 0, Therefore   g' = g – Rω²

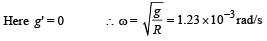
Q.2. A geostationary satellite is orbiting the earth at a height of 6 R above the surface of the earth, where R is the radius of the earth. The time period of another satellite at a height of 2.5 R from the surface of the earth is ..........hours. (1987 - 2 Marks)

Ans. 8.48 hr

Solution. KEY CONCEPT : According to Kepler's law T² ∝R³

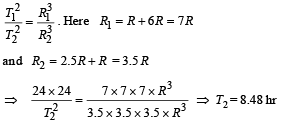
Q.3. The masses and radii of the Earth and the Moon are M₁, R₁ and M₂, R₂ respectively. Their centres are at a distance d apart. The minimum speed with which a particle of mass m should be projected from a point midway between the two centres so as to escape to infinity is ................. (1988 - 2 Marks)

Ans. 

Solution. Increase in P.E. of system

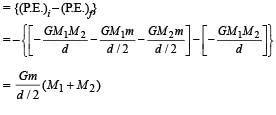
This increase in P.E. is at the expense of  K.E. of mass m

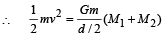
where v is the velocity with which mass m is projected.

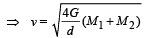
Q.4. A particle is projected vertically upwards from the surface of earth (radius R_e) with a kinetic energy equal to half of the minimum value needed for it to escape. The height to which it rises above the surface of earth is.... (1997 - 2 Marks)

Ans. h = R

Solution.

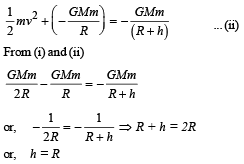
True/False

Q.1. It is possible to put an artificial satellite into orbit in such a way that it will always remain directly over New Delhi.    (1984 - 2 Marks)

Ans. F

Solution. New Delhi is not on the equatorial plane and geostationary satellite is launched on the equatorial plane.