JEE Advanced (Matrix Match): Limits, Continuity & Differentiability | Chapter-wise Tests for JEE Main & Advanced PDF Download
Match the following
DIRECTIONS (Q. 1 and 2) : Each question contains statements given in two columns, which have to be matched. The statements in Column-I are labelled A, B, C and D, while the statements in ColumnII are labelled p, q, r, s and t. Any given statement in Column-I can have correct matching with ONE OR MORE statement(s) in Column-II. The appropriate bubbles corresponding to the answers to these questions have to be darkened as illustrated in the following example : If the correct matches are A-p, s and t; B-q and r; C-p and q; and D-s then the correct darkening of bubbles will look like the given.

Q. 1. In this questions there are entries in columns I and II. Each entry in column I is related to exactly one entry in column II. Write the correct letter from column II against the entry number in column I in your answer book.
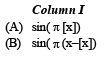

Ans. (A) - p, (B) - r
Solution. 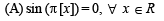
∴ Differentiable everywhere.
∴ (A) → (p)
(B) sin (p (x – [x])) = f (x)
We know that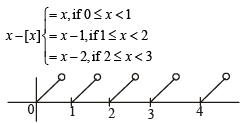
It’s graph is, as shown in figure which is discontinuous at 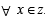 Clearly x – [x] and hence sin (p (x – [x])) is not differentiable
Clearly x – [x] and hence sin (p (x – [x])) is not differentiable 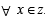
(B) → r
Q. 2. In the following [x] denotes the greatest integer less than or equal to x. Match the functions in Column I with the properties in Column II and indicate your answer by darkening the appropriate bubbles in the 4 × 4 matrix given in the ORS.
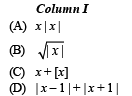
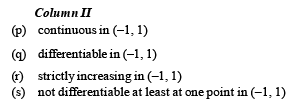
Ans. (A) - p, q, r ; (B) - p, s ; (C) - r, s ; (D) - p, q
Solution.
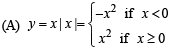
Graph is as follows :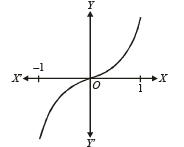
From graph y = x | x | is continuous in (– 1, 1) (p)
differentiable in (– 1, 1) (q)
Strictly increasing in (–1, 1). (r)
(B) 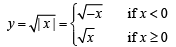
{where y can take only + ve values}
and y2 = x, x > 0
∴ Graph is as follows :
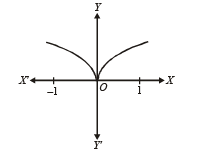
From graph 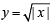 is continuous in (– 1, 1) (p) not differentiable at x = 0 (s)
is continuous in (– 1, 1) (p) not differentiable at x = 0 (s)
(C) NOTE THIS STEP
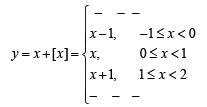
∴ Graph of y = x + [x] is as follows :
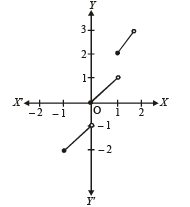
From graph, y = x + [x] is neither con tin uous, nor differentiable at x = 0 and hence in ( – 1, 1). (s)
Also it is strictly increasing in (– 1, 1) (r)
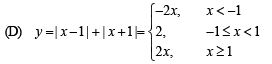
Graph of function is as follows :
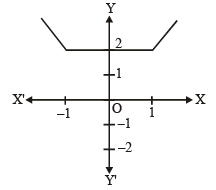
From graph, y = f (x) is continuous (p) and differentiable (q) in (– 1, 1) but not strictly increasing in (– 1, 1).
DIRECTIONS (Q. 3) : Following question has matching lists. The codes for the list have choices (a), (b), (c) and (d) out of which ONLY ONE is correct.
Q. 3. Let f1 : R →R , f2 : [0, ∞)→R, f3 : R →R and f4 :R → [ 0,∞) be defined by 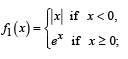
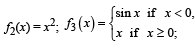
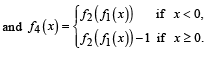



Ans. (d)
Solution:
From graph f is differentiable but not one one.
From graph f2 of1 is neither continuous nor one one.
Integer Value Correct Type
Q. 1. Let f : [1, ∞) → [2, ∞) be a differentiable function such that 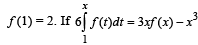 for all x > 1 , then the value of f (2) is
for all x > 1 , then the value of f (2) is
Ans. 6
Solution.
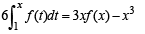
Differentiating, we get 6f (x) = 3 f (x) + 3xf '(x) – 3x2
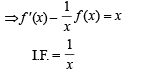
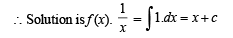
∴ f (x) = x2 + cx
But f (1) = 2 ⇒ c = 1
∴ f (x) = x2 + x
Hence f (2) = 4 + 2 = 6
Note : Putting x = 1 in given integral equation, we get
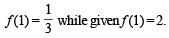
∴ Data given in the question is inconsistent.
Q. 2. The largest value of non-negative integer a for which 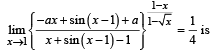
Ans. 2
Solution.
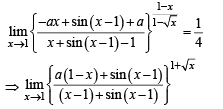
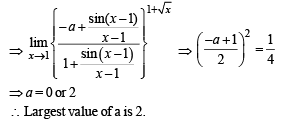
Q. 3. Let f : R →R and g : R → R be r espectively given by f (x) = | x | + 1 and g(x) = x2 + 1. Define h : R → R by
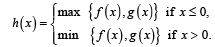
The number of points at which h(x) is not differentiable is
Ans. 3
Solution. 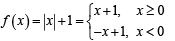
g(x) = x2 + 1
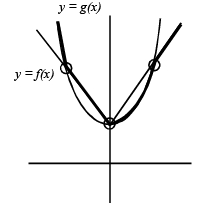
From graph there are 3 points at which h(x) is not differentiable.
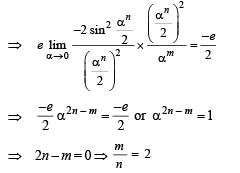
Q. 4. Let m and n be two positive integers greater than 1. If 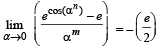 then the value of
then the value of 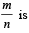
Ans. 2
Solution.
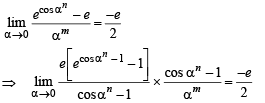
Q. 5. 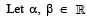 be such that
be such that 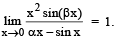 Then 6 (α + β) equals.
Then 6 (α + β) equals.
Ans. 7
Solution.
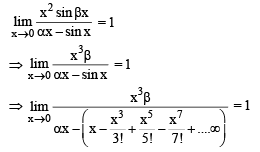
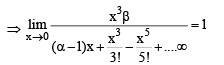
For above to be possible, we should have
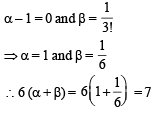
|
481 docs|964 tests
|
















