JEE Advanced (Matrix Match & Integer Answer): Definite Integrals & Applications of Integrals | Chapter-wise Tests for JEE Main & Advanced PDF Download
Match the Following
DIRECTIONS (Q. 1 and 2) : Each question contains statements given in two columns, which have to be matched. The statements in Column-I are labelled A, B, C and D, while the statements in ColumnII are labelled p, q, r, s and t. Any given statement in Column-I can have correct matching with ONE OR MORE statement(s) in Column-II. The appropriate bubbles corresponding to the answers to these questions have to be darkened as illustrated in the following example :
If the correct matches are A-p, s and t; B-q and r; C-p and q; and D-s then the correct darkening of bubbles will look like the given.

Q. 1. Column I Column II
(A) 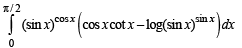 (p) 1
(p) 1
(B) Area bounded by –4y2 = x and x – 1 = –5y2 (q) 0
(C) Cosine of the angle of intersection of curves y = 3x – 1
log x and y = xx – 1is (r) 6 ln 2
(D) Let 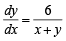 where y(0) = 0 then value of y when
where y(0) = 0 then value of y when
x + y = 6 is (s) 4/3
Ans. (A) - p ; (B) -s ; (C) - p ; (D) - r
Solution.
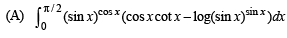
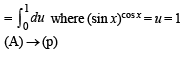
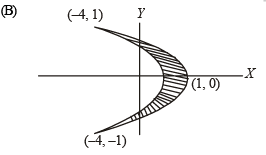
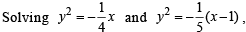 we get intersection points as (– 4, + 1)
we get intersection points as (– 4, + 1)
∴ Required area
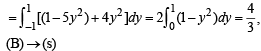
(C) By inspection, the point of intersection of two curves y = 3x–1 log x and y = xx – 1 is (1, 0)
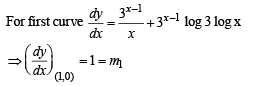
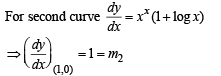
∵ m1 = m2 ⇒ Two curves touch each other
⇒ Angle between them is 0°
∴ cos θ = 1,
(C) ®→ (p)
(D) 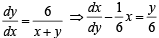
I.F. = e–y/6
⇒ Solution is xe–y/6 = – ye–y/6 – 6e–y/6 + c
⇒ x + y + 6 = cey/6
⇒ x + y + 6 = 6ey/6 ∴ (y (0) = 0)
⇒ 12 = 6ey/6 (using x + y = 6)
⇒ y = 6 ln 2 (D) → (r)
Q. 2. Match the integrals in Column I with the values in Column II and indicate your answer by darkening the appropriate bubbles in the 4 × 4 matrix given in the ORS.
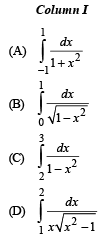
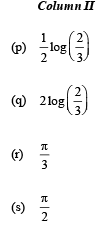
Ans. (A) - s ; (B) -s ; (C) - p ; (D) - r
Solution.
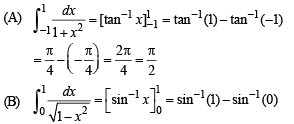
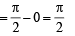
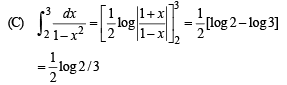
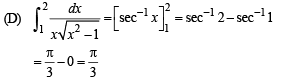
Q. 3. DIRECTIONS (Q. 3) : Following question has matching lists. The codes for the list have choices (a), (b), (c) and (d) out of which ONLY ONE is correct.
List - I List - II
P. The number of polynomials f (x) 1. 8
with non-negative integer coefficients
of degree < 2, satisfying f (0) = 0 and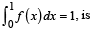
Q. The number of points in the interval 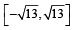 2. 2
2. 2
at which f (x) = sin(x2) + cos(x2) attains its maximum
value, is
R. 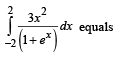 3. 4
3. 4
S. 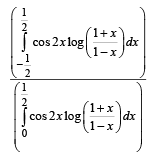 4. 0
4. 0
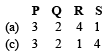
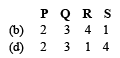
Ans. (d)
Solution. P(2) Let f (x) = ax2 + bx + c
where a, b, c > 0 and a, b, c are integers.
∵ f (0) = 0 ⇒ c = 0
∴f (x) = ax2 + bx
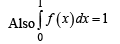
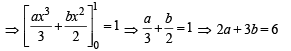
Q∵ a and b are integers
a = 0 and b = 2
or a = 3 and b = 0
∴ There are only 2 solutions.
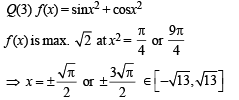
∴ There are four points.
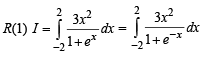
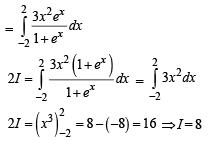
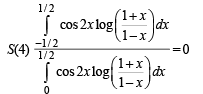
∵ Numerator = 0, function being odd.
Hence option (d) is correct sequence.
|
481 docs|964 tests
|
















