JEE Advanced (Matrix Match & Integer Answer): Rotational Motion | Chapter-wise Tests for JEE Main & Advanced PDF Download
DIRECTIONS (Q. No. 1) : Each question contains statements given in two columns, which have to be matched. The statements in Column-I are labelled A, B, C and D, while the statements in Column-II are labelled p, q, r and s. Any given statement in Column-I can have correct matching with ONE OR MORE statement(s) in Column-II. The appropriate bubbles corresponding to the answers to these questions have to be darkened as illustrated in the following example :

If the correct matches are A-p, s and t; B-q and r; C-p and q; and D-s then the correct darkening of bubbles will look like the given.
Q.1. Column-II shows five systems in which two objects are labelled as X and Y. Also in each case a point P is shown. Column-I gives some statements about X and/or Y. Match these statements to the appropriate system(s) from Column II.
| Column-I | Column II |
| (A) The force exerted by X on Y has a magnitude Mg. | (P)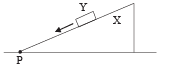 Block Y of mass M left on a fixed inclined plane X, slides on it with a constant velocity. Block Y of mass M left on a fixed inclined plane X, slides on it with a constant velocity. |
(B) The gravitational potential energy of X is continuously increasing. | (Q)
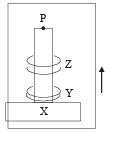
Two ring magnets Y and Z, each of mass M, are kept in frictionless vertical plastic stand so that they repel each other. Y rests on the base X and Z hangs in air in equilibrium. P is the topmost point of the stand on the common axis of the two rings. The whole system is in a lift that is going up with a constant velocity. |
(C) Mechanical energy of the system X +Y is continuously decreasing. | (R)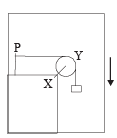 A pulley Y of mass m0 is fixed to a table through a clamp X. A block of mass M hangs from a string that goes over the pulley and is fixed at point P of the table. The whole system is kept in a lift that is going down with a constant velocity. A pulley Y of mass m0 is fixed to a table through a clamp X. A block of mass M hangs from a string that goes over the pulley and is fixed at point P of the table. The whole system is kept in a lift that is going down with a constant velocity. |
| (D) The torque of the weight of Y about point P is zero. | (S)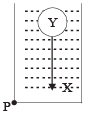 A sphere Y of mass M is put in a non-viscous liquid X kept in a container at rest. The sphere is released and it moves down in the liquid. A sphere Y of mass M is put in a non-viscous liquid X kept in a container at rest. The sphere is released and it moves down in the liquid. |
(T)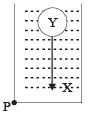 A sphere Y of mass M is falling with its terminal velocity in a viscous liquid X kept in a container. A sphere Y of mass M is falling with its terminal velocity in a viscous liquid X kept in a container. |
Ans. (A) → p, t; (B) → q, s, t; (C) → p, r, t; (D) → q, p
Solution. 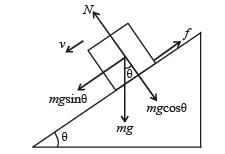
As the velocity is constant
f = mg sinθ ..... (i)
But f = μN = μmg cosθ ..... (ii)
From (i) and (ii)
μmg cosθ = mg sinθ ⇒ m = tanθ
The force by X on Y is the resultant of f and N and is equal to
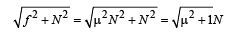
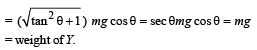
Therefore statement (a) is correct.
Now, due to the presence of frictional force between Y and X, the mechanical energy of the system ( X +Y) decreases continously as Y slides down.
Therefore statement (c) is correct.
(q) As the lift moves up, X also
moves up and therefore the gravitational energy of X is continously increasing. option (b) is correct.
The torque of the weight of Y about P is zero as the perpendicular distance of the line of action of force from the point P is zero.Option (d) is correct.The force exerted by X on Y will be equal to Mg + Mg= 2mg where Mg is wt. of Y and Mg is the force on Y due to Z.
Option (a) is incorrect.
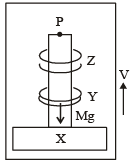
(r) In this case the force exerted by X on Y is same as the force exerted by Y on X. The force on X due to Y is
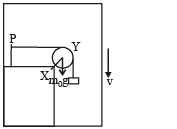
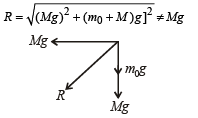
Therefore, option (a) is incorrect.
The mechanical energy of the system (X + Y) is continously decreasing as the system is coming down and its potential energy is decreasing, the kinetic energy remaining the same.
Therefore, option (c) is correct and (b) is incorrect.
The torque of the weight of Y about P is not zero.
(s) The force on Y by X is equal to the wt. of liquid displaced which cannot be equal to Mg as the density of Y is greater than density of X (As Y is sinking) Therefore, option (a) is in correct.
The gravitational potential energy of X increases continously because as Y moves down, the centre of mass of X moves up.
Therfore option (b) is correct.
(t) Sphere Y is moving with terminal velocity. Therefore, the net force on Y is zero i.e.
Mg = B+Fv
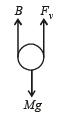
where B = buoyant force and Fv = viscous force.
B + Fv are exerted by X on Y.
Therefore, option (a) is correct.
The gravitational potential energy of X is continously increasing because as Y moves down, the centre of mass of X moves up.
Option [b] is correct.
The mechanical energy of the system (X + Y) is continously decreasing to overcome the viscous forces.
Option (c) is correct.Q.2.
Q.2. A binary star consists of two stars A (mass 2.2Ms) and B (mass 11Ms), where Ms is the mass of the sun. They are separated by distance d and are rotating about their centre of mass, which is stationary. The ratio of the total angular momentum of the binary star to the angular momentum of star B about the centre of mass is
Ans. 6
Solution. Let the center of mass of the binary star system be at the origin. Then
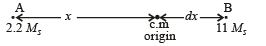
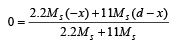
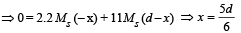
For a binary star system, angular speed w about the centre of mass is same for both the stars.
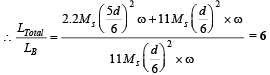
Q.3. A boy is pushing a ring of mass 2 kg and radius 0.5 m with a stick as shown in the figure. The stick applies a force of 2N on the ring and rolls it without slipping with an acceleration of 0.3 m/s2. The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the coefficient of friction between the stick and the ring is (P/10). The value of P is
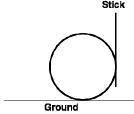
Ans. 4
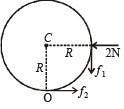
Solution. Under the influence of the force of stick (2N), the point of contact O of the ring with ground tends to slide. But the frictional force f2 does not allow this and creates a torque which starts rolling th e ring. A friction force f1 also acts between the ring & the stick.
Applying Fnet = ma in the horizontal direction. We get

Applying τ = Iα about C we get
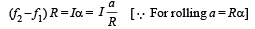
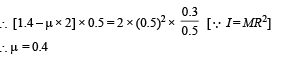
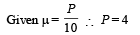
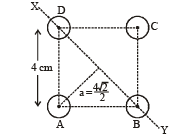
Q.4. Four solid spheres each of diameter √5 cm and mass 0.5 kg are placed with their centers at the corners of a square of side 4 cm. The moment of inertia of the system about the diagonal of the square is N ´ 10–4 kg– m2, then N is
Ans. 9
Solution. Let the four spheres be A, B, C, & D
IXY = I1 + IB + IC + ID = 2 IA + 2IB
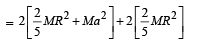
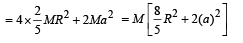
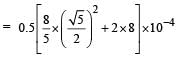
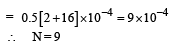
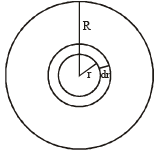
Q.5. A lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure. The moment of inertia of this lamina about axes passing though O and P is IO and IP respectively. Both these axes are perpendicular to the plane of the lamina. The ratio IP / IO to the nearest integer is
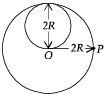
Ans. 3
Solution. Let σ be the surface mass density. Then
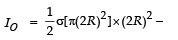
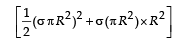
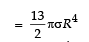
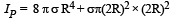
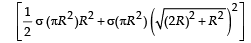
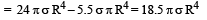
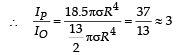
Q.6. A uniform circular disc of mass 50 kg and radius 0.4 m is rotating with an angular velocity of 10 rad s–1 about its own axis, which is vertical. Two uniform circular rings, each of mass 6.25 kg and radius 0.2 m, are gently placed symmetrically on the disc in such a manner that they are touching each other along the axis of the disc and are horizontal. Assume that the friction is large enough such that the rings are at rest relative to the disc and the system rotates about the original axis. The new angular velocity (in rad s–1) of the system is
Ans. 8
Solution. Applying conservation of angular momentum
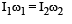
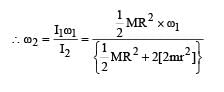
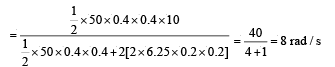
Q.7. A horizontal circular platform of radius 0.5 m and mass 0.45 kg is free to rotate about its axis. Two massless spring toyguns, each carrying a steel ball of mass 0.05 kg are attached to the platform at a distance 0.25 m from the centre on its either sides along its diameter (see figure). Each gun simultaneously fires the balls horizontally and perpendicular to the diameter in opposite directions. After leaving the platform, the balls have horizontal speed of
9 ms–1 with respect to the ground. The rotational speed of the platform in rad s–1 after the balls leave the platform is
Ans. 4
Solution. By conservation of angular momentum
2(mvr) = Iω
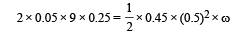
Q.8. A uniform circular disc of mass 1.5 kg and radius 0.5 m is initially at rest on a horizontal frictionless surface. Three forces of equal magnitude F = 0.5 N are applied simultaneously along the three sides of an equilateral triangle XYZ with its vertices on the perimeter of the disc (see figure). One second after applying the forces, the angular speed of the disc in rad s–1 is
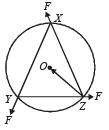
Ans. 2
Solution. 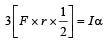
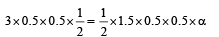
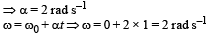
Q.9. Two identical uniform discs roll without slipping on two different surfaces AB and CD (see figure) starting at A and C with linear speeds v1 and v2, respectively, and always remain in contact with the surfaces. If they reach B and D with the same linear speed and v1 = 3 m/s then v2 in m/s is (g = 10 m/s2)
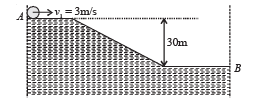
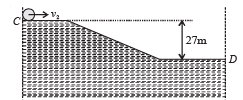
Ans. 7
Solution. Total kinetic energy of a rolling disc
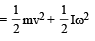
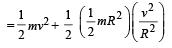
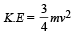
k.Ei + loss in gravitational potential energy = K.Ef
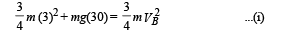
For surface AB
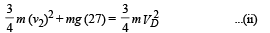
Given VB = VD. Therefore from (i) and (ii)
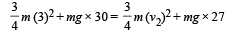
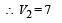
Q.10. The densities of two solid spheres A and B of the same radii R vary with radial distance r 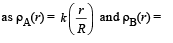
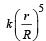
respectively, where k is a constant. The momentsof inertia of the individual spheres about axes passing through their centres are IA and IB, respectively. If , 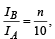
the value of n is
Ans. 6
Solution. 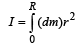
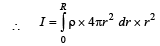
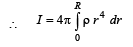
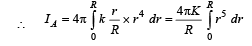
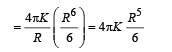
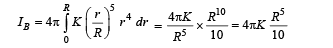
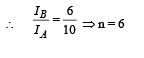
|
481 docs|964 tests
|