JEE Advanced (Matrix Match & Integer Answer): Work, Energy & Power | Chapter-wise Tests for JEE Main & Advanced PDF Download
Match the Following
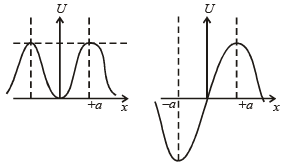
Q.1. A particle of unit mass is moving along the x-axis under the influence of a force and its total energy is conserved. Four possible forms of the potential energy of the particle are given in column I (a and U0 constants). Match the potential energies in column I to the corresponding statement(s) in column II.
| Column I | Column II |
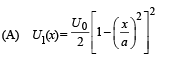 | (p) The force acting on the particle is zero at x = a |
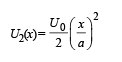 | (q) The force acting on the particle is zero at x = 0 |
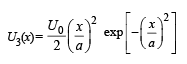 | r) The force acting on the particle is zero at x = – a |
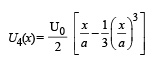 | (s) The particle experiences an attractive force towards x = 0 in the region |x| < a |
(t) The particle with total energy U0/4 can oscillate about the point x = – a |
Ans. (A) p, q, r, t; (B) q, s; (C) p, q, r, s; (D) p, r, t
Solution. A → p, q, r, t; B → q, s; C → p, q, r, s; D → p, r, t
For A
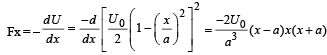
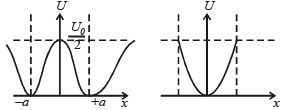
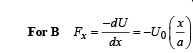
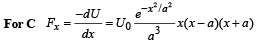
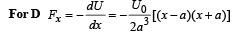
Integer Value Correct Type:-
Q.1. A light inextensible string that goes over a smooth fixed pulley as shown in the figure connects two blocks of masses 0.36 kg and 0.72 kg. Taking g = 10 m/s2, find the work done (in joules) by the string on the block of mass 0.36 kg during the first second after the system is released from rest. (2009)
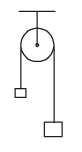
Ans. 8J
Solution.
Given m = 0.36 kg, M = 0.72 kg.
The figure shows the forces on m and M. When the system is released, let the acceleration be a. Then T – mg = ma Mg – T = Ma
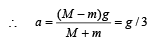
and T = 4 mg/3
For block m :
u = 0, a = g/3, t = 1, s = ?
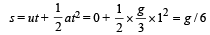
∴ Work done by the string on m is
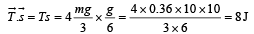
Q.2. Three objects A, B and C are kept in a straight line on a frictionless horizontal surface. These have masses m, 2m and m, respectively. The object A moves towards B with a speed 9 m/s and makes an elastic collision with it. There after, B makes completely inelastic collision with C. All motions occur on the same straight line. Find the final speed (in m/s) of the object C. (2009)
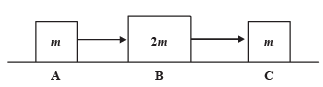
Ans. 4 m/s
Solution. The velocity of B just after collision with A is
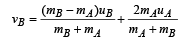
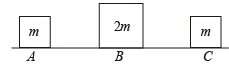
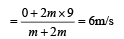
The collision between B and C is completely inelastic.
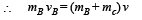
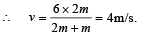
Q.3. A block of mass 0.18 kg is attached to a spring of forceconstant 2 N/m. The coefficient of friction between the block and the floor is 0.1. Initially the block is at rest and the spring is un-stretched. An impulse is given to the block as shown in the figure. The block slides a distance of 0.06 m and comes to rest for the first time. The initial velocity of the block in m/s is V = N/10. Then N is
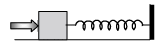 Ans. 4
Ans. 4
Solution. Let v be the speed of the block just after impulse. At B, the block comes to rest. Therefore
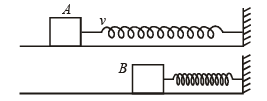
Loss in K.E. of the block = Gain in P.E. of the spring + Work done against friction
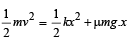
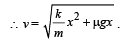
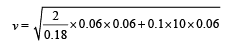

Q.4. A particle of mass 0.2 kg is moving in one dimension under a force that delivers a constant power 0.5 W to the particle. If the initial speed (in ms–1) of the particle is zero, the speed (in ms–1) after 5 s is
Ans. 5
Solution. 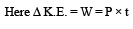
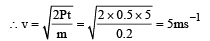
Q.5. Consider an elliptical shaped rail PQ in the vertical plane with OP = 3 m and OQ = 4 m. A block of mass 1 kg is pulled along the rail from P to Q with a force of 18 N, which is always parallel to line PQ (see the figure given). Assuming no frictionless losses, the kinetic energy of the block when it reaches Q is (n × 10) joules. The value of n is (take acceleration due to gravity = 10 ms–2)
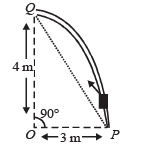
Ans. 5
Solution. Work done = Increase in potential energy + gain in kinetic energy
F × d = mgh + gain in K.E.
18 × 5 = 1 × 10 × 4 + gain in K.E.
∴ Gain in K.E. = 50 J = 10n
∴ n = 5
|
481 docs|964 tests
|





















