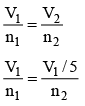JEE Advanced (One or More Correct Option): Heat & Thermodynamics | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. Temperature of 1000 grams of nitrogen is raised from – 20ºC to 100ºC at constant pressure. Given: specific heat at constant volume Cv = 5 cal/mole ºC and R = 2Cal/mole ºC
(a) Heat required in the process is 30 K Cal
(b) Increase in the internal energy of gas is 21 Kcal
(c) If process is at constant volume then heat required is 21 Kcal
(d) external work done is 10 KCal
Correct Answer is option (a, b, and c)
(a) Heat required is - Q = nCpΔT = n(Cv + R)ΔT= 1000/28 [5 + 2] × 120 = 30 × 103 cal
Q = 30 Kcal
(b) The increase in the internal energy is ΔU = nCvΔT = 1000/28 × 5 × 120 = 21 Kcal
(c) Q = nCvΔT + PΔV for constant volume ΔV = 0
Q = nCvΔT = 21 Kcal
(d) external work done is W = Q - ΔU = 8.6 KCal
Q.2. 10 litres of ideal gas at atmospheric pressure is compressed isothermally to volume of 1 litre and then allowed to expand adiabatically to 10 litres. Choose the correct options related to this
(a) Net work is done on gas.
(b) Net work is done by gas.
(c) Final pressure is equal to initial pressure.
(d) final pressure is less than initial pressure.
Correct Answer is option (a and d)
AB: isotherm BC : adiabat
Area under AB curve is more than BC Curve hence het work done is negative and hence work is done on system (gas). As can be seen from graph Pf final pressure is less than initial pressure Pi i.e Pf < Pi
Q.3. Figure shows an indicator diagram. During path 1–2–3, 100 cal is given to the system and 40 cal worth work is done. During path 1 – 4 –3, the wore done is 10 cal. Then: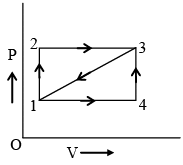 (a) heat given to the system during path 1–4–3 is 70 cal.
(a) heat given to the system during path 1–4–3 is 70 cal.
(b) if the system is brought from 3 to 1 along straight line path 3 –1, work done is worth 25 cal.
(c) along straight line path 3–1 the heat ejected by the system is 85 cal.
(d) the internal energy of the system in state 3 is 140 cal above that in state 1.
Correct Answer is option (a, b and c)
The critical step is that work in path 1-3 is mean of that for 1-2-3 and 1-4-3 (considering areas).
For (A) 100 – 40 = x – 10 or, x = 70 cal.
(b) It is also correct as half of (40 + 10) is 25 cal.
(c) dU is –60, work is – 25
So, – 60 = dQ – (–25)
or, dQ = – 85 cal
Hence, option (C) is also correct.
(d) dU = 100 – 40 = 60 cal
Hence, option (D) is not correct.
Q.4. Figure shows two paths that may be taken by gas from an initial point i to final point f. Path 1 consists of an isothermal expansion (work is 50 J in magnitude), an adiabatic expansion (work is 40 J in magnitude), & then an adiabatic compression (work is 25 J in magnitude) –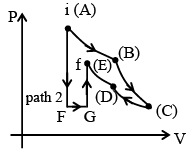 (a) Change in internal energy in path 2, i.e. n path AFGE is – 15J.
(a) Change in internal energy in path 2, i.e. n path AFGE is – 15J.
(b) Heat transferred in path AB is 50 J.
(c) Internal energy change in path DE is – 15 J.
(d) Work done is greatest in path FG.
Correct Answer is option (a and b)
ΔUAB + ΔUBC + ΔUCD + ΔUDE = ΔUif
0 + (- WBC) + 0 + (- WDE) = ΔUif
- 40 J + (- (- 25)) = ΔUif
- 40 + 25 = ΔUif
ΔUif = - 15 J
For path AB : Isothermal process QAB = WAB = 50 J
Q.5. AB: isothermal (TA = 300 K)
BC: Adiabatic (Work = 5 J)
CD: Constant pressure (5 atm)
DE: Isothermal
EA: Adiabatic (Change in internal energy 8J) –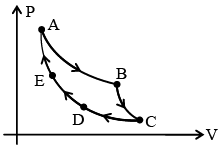 (a) work done in the cycle is 13 J.
(a) work done in the cycle is 13 J.
(b) change in internal energy in path CD is – 3J.
(c) heat transferred in path DE is –11J.
(d) work done in EA is – 8J.
Correct Answer is option (a and b)
ΔUAB + ΔUBC + ΔUCD + ΔUDE + ΔUEA = 0
0 + (– WBC) + ΔUCD + 0 + (8J) = 0
(– 5J) + ΔUCD + (8J) = 0ΔUCD = - 3J
QAB + QBC + QCD + QDE + QEA = WAB + WBC + WCD + WDE + WEA
(QCD – WCD) + QEA = WBC + WEA
– 3J – WBC = WEA
– 3J – 5J = WEA
WEA = – 8J
Q.6. A gas is taken through a cyclic process. The change in internal energy along the path from c to a is – 160 J. Heat transferred along the path from a to b is 200 J and 40 J from path b to c. Then-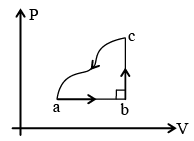 (a) work done in the cycle is less than 80 J.
(a) work done in the cycle is less than 80 J.
(b) work done in path abc is 80 J.
(c) work done in path ab is 160 J.
(d) net heat transferred is less than 80 J.
Correct Answer is option (a, b and b)
For cyclic process Qnet = Wnet since Ucycle = 0
Qab + Qbc + Qca = Wab + Wbc + Wca
200 J + 40 J + Qca = Wabc + Wca
240 J + Qca = Wabc + Wca
240 J + Qca – Wca = Wabc
240 – 160 = Wabc
Wab + Wbc = Wabc = 80 J
Wab + 0 = 80 J
Wab = 80 J
Wnet = Wab + Wbc + Wca
Since Wca < 0, Wnet < 80 J
Q.7. Figure shows ‘P’ vs ‘T’ diagram for cyclic process ABCA undergone by ideal gas. Which of the following graph is correct (U: internal energy) –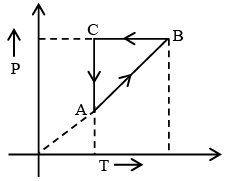
(a) 
(b) 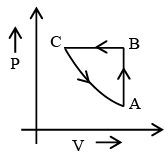
(c) 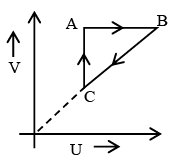
(d) 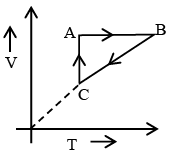
Correct Answer is option (b and c)
AB: Isochoric process with increase in P and T.
BC: Isobaric process with decrease in T and V.
CA: Isothermal process with decrease in P and hence increase in V.
Q.8. A certain mass of saturated water vapour is contained in a cylindrical vessel under a weightless piston at one atmospheric pressure. The piston is slowly lowered till 0.7 g of vapour gets condensed. The volume under the piston is now only (1/5)th of the original volume. (Neglect the volume of liquid formed). Then -
(a) original mass of the vapour was 0.89 gm.
(b) original mass of the vapour was 1.14gm
(c) temperature of vapour is 100ºC.
(d) temperature of vapour is 114ºC.
Correct Answer is option (a and c)
P1V1 = n1RT
P1 = vapour pressure = P0
If piston is lowered slowly, then the process is isothermal
n2 = n1/5
0.7 gm vapour is condensed so
n – n2 = 0.7/18 …(i)n1 = m/18 …(ii)
Dividing (i) by (ii),
4m = 3.5
m = 3.5/4 = 0.87
Q.9. An ideal gas undergoes an expansion from a state with temperature T, and volume V1 to V2 through three different polytropic processes A, B and C as shown in the P–V diagram. If |DEA|, |DEB| and |DEC| be the magnitude of changes in internal energy along the three paths respectively -
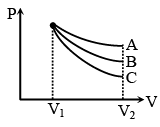
(a) |ΔEA| < |ΔEB| < |ΔEC| if temperature in every process decreases.
(b) |ΔEA| > |ΔEB| > |ΔEC| if temperature in every process decreases.
(c) |ΔEA| > |ΔEB| > |ΔEC| if temperature in every process increases.
(d) |ΔEB| < |ΔEA| < |ΔEC| if temperature in every process increases.
Correct Answer is option (a and c)
If T1 > T2
then E0 > Ef
Hence (E0 – EA) < (E0 – EB) < E0 – EC
|ΔEA| < |ΔEB| < |ΔEC|If T1 < T2 then E0 < Ef for all the processes
|ΔEA| > |ΔEB| > |ΔEC|
Q.10. For the PV diagram shown, for path 1-2-3, 100 J of heat is given to the system and 40 J of work is done by the system. For path 1-4-3 the work done by system is 10 J. Then -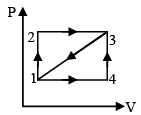 (a) U3 – U1 = 60 joule, where U3 & U1 are internal energy of gas
(a) U3 – U1 = 60 joule, where U3 & U1 are internal energy of gas
(b) for path 3→ 1 the heat is rejected and equal to 85 joule
(c) for path 1→ 4 the work done by system is 10 joule
(d) for path 1→ 4 the heat given to system is 20 joule
Correct Answer is option (a, b and c)
Path - 1,2,3,
ΔQ = ΔU + ΔW, 100 = ΔU + 40
DU = 60 joule = U3 - U1
Path 1 - 4
W by gas = W by gas 1-4-3 = 10 joule
W for process 3 → 1 =10 = 25 joule
Q = – 25 – 60 = – 85 joule
|
446 docs|929 tests
|