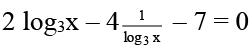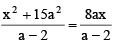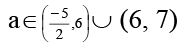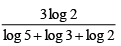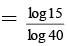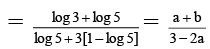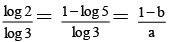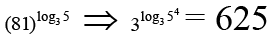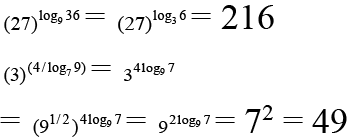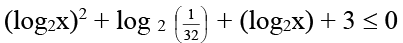JEE Advanced (One or More Correct Option): Logarithms | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. If a ≠ 0 then the inequation |x – a| + |x + a| < b
(a) Has no solution if b ≤ 2 |a|
(b) Has a solution set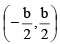if b > 2 |a|
(c) Has a solution set 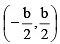if b < 2 |a|
(d) Has no solution if b > 2|a|

Correct Answer is option (a and b)
If a > 0
2x < b if x > a
2a < b if – a < x < a
– 2x < b if x < – a
If a < 0    Þ 2x < - a if x > - a
– 2a < b if  a < x < – a
– 2x < b   if x < a
Hence b > 2|a| if – a < x < a
⇒ b > 2|a| if  ⇒ B is true  and for
b ≤ 2|a| hence no solution  
So A, B are true.

Q.2. If log_ax = b for permissible values of a & x then which is/are correct
(a) If a & b are true irrational numbers then x can be rational    
(b) If a is rational & b is irrational then x can be rational
(c) If a is irrational & b is rational then x can be rational
(d) If a is rational & b is rational then x can be rational

Correct Answer is option (a, b, c and b)
(A)  ∴ x = a^b
If a = (√2)^√2 irrational
b = √2 irrational
then a^b = ((√2)^√2)^√2 = 2 which is rational
(B) If a = 2  ∈Q
b =  log₂ 3 ∉Q
then a^b = 3  ∈ Q
C & D can be easily checked

Q.3. The x-values satisfying the equation 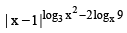=  (x – 1)⁷ is/are
(a) 1/√3
(b) 1
(c) 2
(d) 81

Correct Answer is option (c and d)
L.H.S. + ve ⇒ x > 1
So log₃ x² – 2log_x9 = 7  or x –1=1 ⇒ x = 2

2(log₃x)² – 7 log₃x – 4 = 0    ⇒ log₃x = -1/2, 4
x = 3^–1/2, 3⁴

1/√3 neglect because x > 1
So x = 2, 81

Q.4. If x = 9 is solution of λn (x² +15a²)   -λn (a - 2) = λn (8ax/a-2) then
(a) a = 3/5
(b) a = 3
(c) x = 15
(d) x = 2

Correct Answer is option (b and c)
Θ a > 2 
Also 8ax/a-2 > 0
∴ x > 0     as    a > 2
Now

⇒ x² – 8ax + 15a² = 0
⇒ x = 3a, 5a
∴ x = 9 (given)
⇒ x = 3, 9/5
But a > 2
∴ a = 3
at    a = 3   ⇒  x = 9, 15

Q.5. If y = log_7–a (2x² + 2x + a + 3) is defined 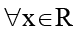 then possible integer value of a is/are
(a) 4  
(b) – 3
(c) – 2
(d) 5

Correct Answer is option (a, c and d)
Θ 2x² + 2x + a + 3 > 0
∴ D < 0
⇒ a  > -5/2   ... (1)
Also     7 – a > 0
⇒ a < 7 ……(ii)
&         7 – a ≠ 1
a ≠ 6 ……(iii)  
from (i) (ii) & (iii)  

Q.6. In which of the following m > n (m, n ∈ R)
(a) m = (log₂5)² & n = log ₂20
(b) m = log₁₀2 & n = log₁₀ 3√10
(c) m = log₁₀5. log₁₀20 + (log₁₀2)² & n = 1
(d) m = log_1/2 (1/3) & n = log_{1/3 (1/2)}

Correct Answer is option (a and d)
(A) m – n = (log₂5)² – (log₂5 + 2) = (log₂5 – 2) (log₂5 + 1) > 0
∴ m > n
(B) m = 0·3010,    n = 1/3 ∴ m < n
(C)  m =(1 – log₁₀2)(1 + log₁₀2) = 1– log²₁₀2 < 1
(D) m = log₂3,  n = log₃2 ∴ m > n

Q.7. If log₁₀5 = a and log₁₀3 = b then
(b) log₃₀ 8 =
(b) log₄₀ 15 =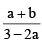
(c) log₂₄₃32 =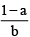
(d) All above

Correct Answer is option (a, b, c and d)
(A) log₃₀ 8 =
But log 2 = 1 – log 5 = 3 (1 – a) /(b + 1)
Hence choice [A] is true.
(B) log₄₀15

Hence choice [B] is true.
(C) log₂₄₃ 32 =
Hence choice [C] is true.
Thus correct choice are (A),(B), (C) and (D)

Q.8. Which among the following are true?
(a)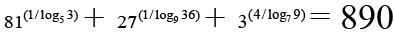
(b)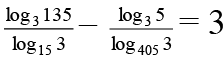
(c)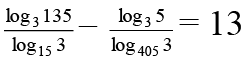
(d) All above

Correct Answer is option (a and b)
(A)

So sum = 890
⇒ Choice [A] is true.
(B) [log₃(3³ × 5)]. [log₃ (3×5)] – log₃5 [log₃(3⁴ × 5)] = 3
⇒ choice [B] is true.
If (B) is true (C) can’t be true.

Q.9. The inequation (log_x2) (log_2x2) (log₂4x) >1
(a) Has a meaning for all x
(b) Has a meaning if x > 2
(c) is satisfied in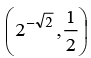
(d) is satisfied in (1, 2^√2)

Correct Answer is option (b, c and d)
log_x 2 is defined x > 0 and x ≠ 3
log_2x 2 is defined x > 0 and x ≠ 1/2
log₂4x is defined x > 0
⇒ domain of function
(A) (log_x2) (log_4x2) (log₂4x) is x > 0
and x ≠ 1 and x ≠ 1/2
So choice [A] is ruled out.
(B) Since x > 2 is sub-set of domain f g(x).
So choice (B) is true.
Given expressions  1 put log2 x = t

If numerator and denominator > 0
⇒ t² + t –t –2 < 0
⇒ – √2 < t < √2
⇒ 2^–√2 < x < 2^√2
Choices (C) and (D) are satisfied

Q.10. Integers satisfying the inequality log₂² x + log₂ 0.03125x + 3 ≤ 0 is/are –
(a) – 1
(b) 0
(c) 2
(d) 1

Correct Answer is option (c and d)

⇒ (log2x)² + (log₂x) - 2 ≤ 0
⇒ (log₂x + 2) (log₂x - 1) ≤ 0
⇒ - 2 ≤ log₂x ≤ 1
⇒ 1/4 ≤ x ≤ 2
So integers are x = 1, 2