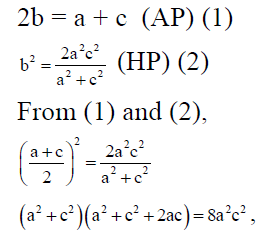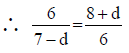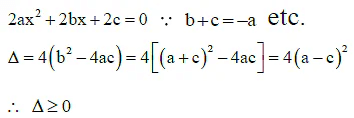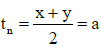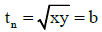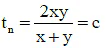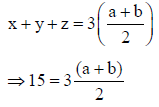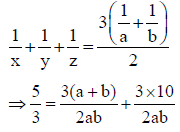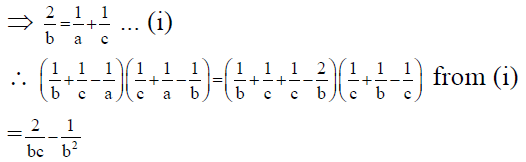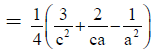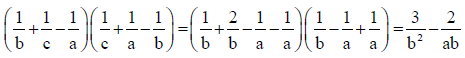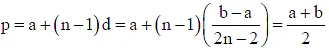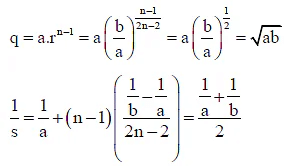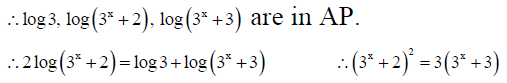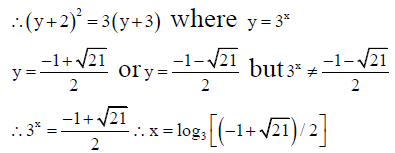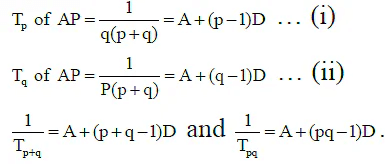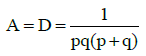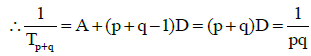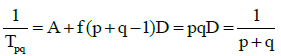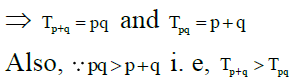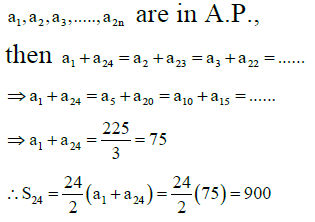JEE Advanced (One or More Correct Option): Sequences & Series | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. If a, b, c are in A. P., and a², b², c² are in H. P., then
(a) a = b = c
(b)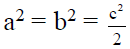
(c) a, b, c are in G. P.
(d) -a/2, b, c are in G.P

Correct Answer is option (a, c , d)

On solving we get a = c

from b = a, a = b = c.

Q.2. The sum of three numbers which are consecutive terms of an A.P. is 21. If the second number is reduced by 1 while the third is increased by 1, three consecutive terms of a G.P. result. The three numbers is
(a) 3, 7, 11
(b) 12, 7, 2

(c) 1, 7, 11
(d) none of these

Correct Answer is option (a, b)

Let the three numbers in A.P. be a - d, a, a + d

Given (a - d) + a + (a + d) = 21

⇒ 3a = 21, ∴ a = 21 ÷  3 = 7
∴ The numbers are 7 - d, 7, 7 + d
If the second number is reduced by 1 while the third number is increased by 1, the resulting numbers are 7 - d, 6, 8 + d which are given to be in G.P.

⇒ 36 = (7 - d) (8 + d) ⇒ 36 = 56 - d - d²
⇒ d² + d - 20 = 0
⇒ (d + 5) (d - 4) = 0 ∴ d = -5, 4
When d = -5
The numbers are 12, 7, 2
When d = 4, the numbers are 3, 7, 11.

Q.3. If a,a² + 2,a³ +10 be three consecutive terms of G.P., then the fourth term is
(a) 0
(b) 6
(c) 729/16
(d) 54

Correct Answer is option (c, d)
The given equation can be written as

∴ Roots are real in any case and may be equal or unequal.

Q.4. If the first and the (2n -1)^th term of an AP, GP and HP are equal and their n^th terms are a, b and c respectively then
(a) a = b = c
(b) a ≥ b ≥ c
(c) a +c = b
(d) ac - b² = 0

Correct Answer is option (a, b, d)

Since, first and (2n – 1)th terms are equal.
Let first term be x and (2n – 1)th term by y.

Whose middle term is t_n .
Thus in arithmetic progression;
In geometric progression;

In harmonic progression;
⇒ b² = ac and a> b > c (Using AM > GM > HM)
Here, equality holds (ie, a = b = c) only if all terms are same.
Hence, option (A), (B) and (D) are correct.

Q.5. Given that x + y+ z =15 when a, x, y, z, b are in A.P. , and 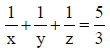 when a, x, y, z, b are in H.P. Then
(a) G.M. of a and b is 3
(b) One possible value of a + 2b is 11
(c) A.M. or a and b is 6
(d) Greatest value of a - b is 8

Correct Answer is option (a, b, d)

⇒ a +b =10     .....(1)

⇒ ab = 9    .....(2)
From (1) & (2) a = 9, b = 1 or a = 1, b = 9
Hence, G.M. = √ab = 3, a + 2b = 11 or 19

Q.6. If a, b, c are in H.P., then the value of 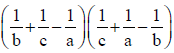 is
(a)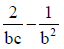
(b)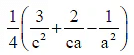
(c)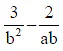
(d) none of these

Correct Answer is option (a, b, c)

As a, b, c are in H.P.

⇒ 1/a, 1/b, 1/c are in A.P.

Also,
    from (i)

Also,

Q.7. If the first and (2n-1)^th terms of an A.P; a G.P. and H.P. are equal and their n^th terms are p, q and s respectively, then which of the following options is/are correct?
(a) p ≥ q ≥ s
(b) p+s = q
(c) ps = q²
(d) p = q = s

Correct Answer is option (a, c)

Let the first term be a and (2n-1)^th term be b then


p, q, r are the A.M, G.M, H.M of a, b.
∴ p ≥ q ≥ r and ps = q²

Q.8. If log3, log(3^x+2), log(3^x+3) are in A.P. Then x is given by
(a)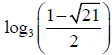
(b)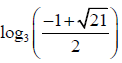
(c)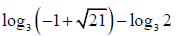
(d)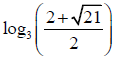

Correct Answer is option (b, c)

Q.9. The p_th term T_p of HP is q(p + q) and q_th term T_q is p (p + q) when p > 1, q > 1, (p ≠ q) then
(a) T_P+Q = PQ
(b) T_PQ = P+Q
(c) T_P+Q > T_PQ
(d) T_PQ > T_P+Q

Correct Answer is option (a, b, c)

Now, solving Eqs. (i) and (ii), we get


and

Q.10. If a₁ ,a₂ ,a₃ .......,a₂₄ be the terms of an A.P. such that a₁ + a₅+ a₁₀ + a₁₅ + a₂₀ + a₂₄ =  225, then
(a) a₁ + a₂₄ = 90
(b) a₁+ a₂₄ = 75
(c) S₂₄ = 900
(d) S₂₄ = 750

Correct Answer is option (b, c)