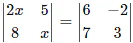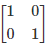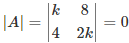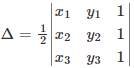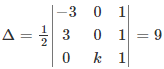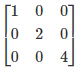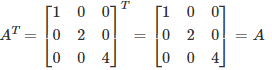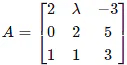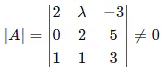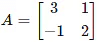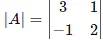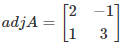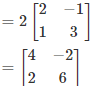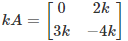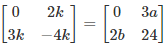JEE Advanced (Single Correct Type): Matrices & Determinants | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1.  If A is a square matrix such that A2 = A, then (I – A)3 + A is equal to
(a) I
(b) 0
(c) I – A
(d) I + A

Correct Answer is option (a)
Given that, A is a square matrix and A² = A.
Consider (I + A)³, where I is the identity matrix.
Using the identity of (a + b)³ = a³ + b³ + 3ab (a + b), we get;
(I + A)³ = I³ + A³ + 3A²I + 3AI²
= I + A²(A) + 3AI + 3A
= I + A² + 3A + 3A
= 7A + I {since it is given that A² = A}
So, (I + A)³ = 7A + I….(1)
Now,
(I + A)³ – 7A = 7A + I – 7A [From (1)]
= I

Q.2.  If, 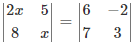 then the value of x is
(a) 3
(b) ±3
(c) ±6
(d) 6

Correct Answer is option (c)
Given,

So, (2x)(x) – (5)(8) = (6)(3) – (-2)(7)
2x² – 40 = 18 + 14
2x² = 32 + 40
2x² = 72
x² = 36
x = √36 = ±6

Q.3. If A = [a_ij] is a square matrix of order 2 such that a_ij = 1, when i ≠ j and a_ij = 0, when i = j, then A² is
(a)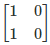
 
(b)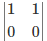

(c)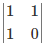

(d)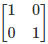

Correct Answer is option (d)
Given,
A = [a_ij] is a square matrix of order 2 such that a_ij = 1, when i ≠ j and a_ij = 0, when i = j.
So, a₁₁ = 0, a₁₂ = 1, a₂₁ = 1 and a₂₂ = 0.
Thus,

A² = A.A
A² =
=
=

Q.4. Value of k, for which 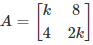 is a singular matrix is
(a) 4
(b) -4
(c) ±4
(d) 0

Correct Answer is option (c)
Given that matrix A is singular.
Thus, the determinant of A is 0.
So,

k(2k) – 8(4) = 0
2k² – 32 = 0
2k² = 32
k² = 16
k = ±4

Q.5. Total number of possible matrices of order 3 × 3 with each entry 2 or 0 is
(a) 9
(b) 27
(c) 81
(d) 512

Correct Answer is option (d)
We know that a matrix 3× 3 contains 9 elements.
Given that each entry of this 3× 3 matrix is either 0 or 2.
Thus, by simple counting principle, we can calculate the total number of possible matrices as:
Total number of possible matrices = Total number of ways in which 9 elements can take possible values
= 2⁹
= 512

Q.6. If A is a square matrix of order 3 and |A| = 5, then the value of |2A′| is
(a) -10
(b) 10
(c) -40
(d) 40

Correct Answer is option (d)
According to the property of transpose of a matrix,
(kA′) = kA′
Also, from the property of determinant of a matrix,
|A′| = |A|
Thus, |2A′| = 2|A|
= 2 × 5
= 10

Q.7. If A and B are two matrices of the order 3 × m and 3 × n, respectively, and m = n, then the order of matrix (5A – 2B) is
(a) m × 3
(b) 3 × 3
(c) m × n
(d) 3 × n

Correct Answer is option (d)
Given that, the order of matrix A is 3 × m, and the order of B is 3 × n.
Also, m = n.
So, the order of matrix A and B is the same, i.e. 3 × m.
Thus, subtraction of matrices is possible and (5A – 3B) also has the same order, i.e. 3 × n.

Q.8. The area of a triangle with vertices (–3, 0), (3, 0) and (0, k) is 9 sq. units. The value of k will be
(a) 9
(b) 3
(c) -9
(d) 6

Correct Answer is option (b)
The formula of area of the triangle with vertices (x₁, y₁), (x₂, y₂), (x₃, y₃) is given by:

Thus, the area of a triangle with vertices (–3, 0), (3, 0) and (0, k) is:

⇒ -3(0 – k) – 0+ 1(3k – 0) = 18
⇒ 3k + 3k = 18
⇒ 6k = 18
⇒ k = 3

Q.9. If 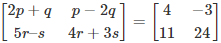 , then the value of p + q – r + 2s is
(a) 8
(b) 10
(c) 4
(d) -8

Correct Answer is option (a)
Given,

Now, by equating the corresponding elements of these two matrices, we get;
2p + q = 4….(1)
p – 2q = -3….(2)
5r – s = 11….(3)
4r + 3s = 24….(4)
By equ (1) × 2 + equ (2), we get;
4p + 2q + p – 2q = 8 – 3
5p = 5
p = 1
Substituting p = 1 in (1),
2 + q = 4
q = 4 – 2 = 2
By equ (3) × 3 + equ (4), we get;
15r – 3s + 4r + 3s = 33 + 24
19r = 57
r = 3
Substituting r = 3 in (3),
15 – s = 11
s = 15 – 11 = 4
Now,
p + q – r + 2s = 1 + 2 – 3 + 2(4) = 8

Q.10. Given that A is a square matrix of order 3 and |A| = -4, then |adj A| is equal to
(a) -4
(b) 4
(c) -16
(d) 16

Correct Answer is option (d)
Given that A is a square matrix of order 3 and |A| = -4.
We know that |adj A| = |A|ⁿ⁻¹, where n is the order of matrix A.
So, |adj A| = (−4)^3-1 = (-4)² = 16

Q.11. The matrix 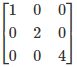 is a
(a) identity matrix
(b) symmetric matrix
(c) skew symmetric matrix
(d) none of these

Correct Answer is option (b)
Let the given matrix be:
A =
Let us find the transpose of A.

Therefore, A is a symmetric matrix.

Q.12. If 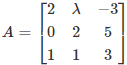 , then A^-1 exists if
(a) λ = 2
(b) λ ≠ 2
(c) λ ≠ – 2
(d) None of these

Correct Answer is option (d)
Given,

The inverse of a matrix exists if its determinant is not equal to 0.
Consider,

⇒ |A| = 2 (6 – 5) – λ (0 – 5) + (-3) (0 – 2) ≠ 0
⇒ 2 + 5λ + 6 ≠ 0
⇒ 5λ + 8 ≠ 0
⇒ 5λ ≠ -8
⇒ λ ≠ -8/5
Therefore, A-1 exists if and only if λ ≠ -8/5.

Q.13. For any two matrices A and B, we have
(a) AB = BA
(b) AB ≠ BA
(c) AB = O
(d) None of the above

Correct Answer is option (d)
For any two matrices A and B,
AB = BA and AB ≠ BA are not valid unless they follow the condition of matrix multiplication.
Also, AB = O is not true in all cases.

Q.14. Which of the following is correct?
(a) Determinant is a square matrix.
(b) Determinant is a number associated with a matrix.
(c) Determinant is a number associated with a square matrix.
(d) None of these

Correct Answer is option (c)
We know that we can calculate determinant values only for square matrices.
Therefore, the determinant is a number associated with a square matrix.

Q.15. If A and B are symmetric matrices of the same order, then (AB′ –BA′) is a
(a) Skew symmetric matrix
(b) Null matrix
(c) Symmetric matrix
(d) None of these

Correct Answer is option (a)
Given that A and B are symmetric matrices of the same order.
Let’s find the transpose of (AB′ –BA′)
(AB′ –BA′)′ = (AB′)′ – (BA′)
= (BA′ – AB′)
= – (AB′ –BA′)
As (AB′ –BA′)′ = – (AB′ –BA′), the matrix (AB′ –BA′) is skew symmetric.

Q.16. Given that A = [a_ij] is a square matrix of order 3×3 and |A| = -7, then the value of ∑_i=1³ a_i2 A_i2, where A_ij denotes the cofactor of element a_ij is
(a) 7
(b) -7
(c) 0
(d) 49

Correct Answer is option (b)
Given,
|A| = -7
Order of matrix A is 3×3.
Now, ∑_i=1³ a_i2 A_i2 = a₁₂ A₁₂ + a₂₂ A₂₂ + a₃₂ A₃₂
= |A|
= -7

Q.17. If A is an invertible matrix of order 2, then det (A^–1) is equal to
(a) det (A)
(b) 1/det (A)
(c) 1
(d) 0

Correct Answer is option (b)
Given that the A is an invertible matrix of order 2.
If the matrix is invertible, then its determinant is not equal to 0.
We know that,
AA^-1 = I, where I is the identity matrix
Taking determinant on both sides,
|AA^-1| = |I|
|A| |A^-1| = 1
|A^-1| = 1/|A| {since A is non-singular, |A| ≠ 0}
Or
det(A^-1) = 1/det(A)

Q.18. If A is a skew-symmetric matrix, then A2 is a
(a) Skew symmetric matrix
(b) Symmetric matrix
(c) Null matrix
(d) Cannot be determined

Correct Answer is option (b)
Given that A is a skew-symmetric matrix, so A′ =-A.
Consider the transpose of A².
(A²)′ = (AA)′
= A′A′
=(-A)(-A)
= A²
⇒ (A²)′ = A²
Therefore, A² is a symmetric matrix.

Q.19. If 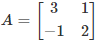 , then 14A-1 is given by:
(a)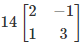

(b)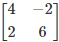

(c)

(d)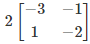

Correct Answer is option (b)
Given,

So,

= (3)(2) – (-1)(1)
= 6 + 1
= 7
Now,

14A^-1 = 14[adj A/ |A|] = (14/7) adj A
= 2 adj A

Q.10. If 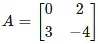 and 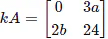 , then the values of k, a and b respectively are
(a) -6, -12, -18
(b) -6, -4, -9
(c) -6, 4, 9
(d) -6, 12, 18

Correct Answer is option (b)
Given,
 and
Now,

Thus

By equating the corresponding elements,
-4k = 24
k = -6
Also, 2k = 3a
2(-6) = 3a
3a = -12
a = -4
And
3k = 2b
3(-6) = 2b
2b = -18
b = -9
Therefore, k = -6, a = -4, and b = -9.