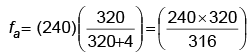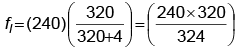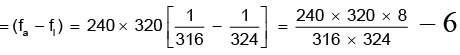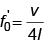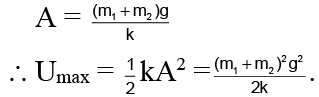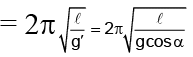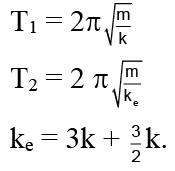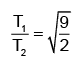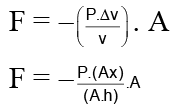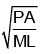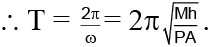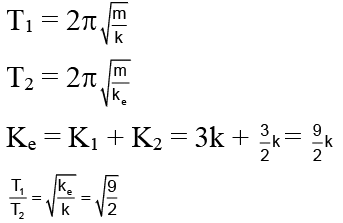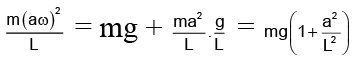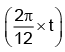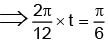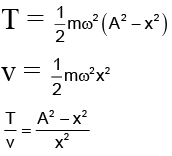JEE Advanced (Single Correct Type): Simple Harmonic Motion (Oscillation) | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. Two small loud speakers A, B, 1.00 m apart are connected to the same oscillator so that both emit sound waves of a definite frequency in phase. A sensitive detector, moving parallel to AB along PQ, 2.40 m away (see Figure) detects a maximum wave at P on the perpendicular bisector MP of AB and another maximum wave when it first reaches a point Q directly opposite to B. The velocity of the sound waves is340 ms–1. The frequency of the oscillator is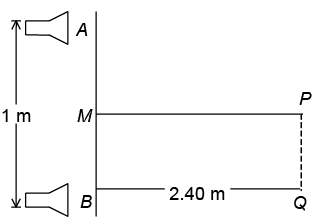 (a) 1500 Hz
(a) 1500 Hz
(b) 1700 Hz
(c) 3400 Hz
(d) 800 Hz
Correct Answer is option (b)
Since, Q is the first maximum after P, AQ – BQ = λ
BQ = 2.4 m, AB = 1.0 m, ABQ = 90°
Hence AQ =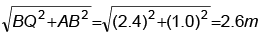
Also λ = 2.60 - 2.40 = 0.20 m
Hence, wave speed, C = 340 = f .λ = f ×(0.20)
Hence, frequency, f = 340/0.20 = 1,700 Hz
Q.2. The engine of a train has just completed a long U-bend of a track. The guard-van is just entering the bend, which is an exact semi-circle (see figure). The driver blows the whistle of the train located in front of the engine to warn a workman on the track ahead. The whistle has a frequency of 400 Hz and the speed of the train is 17 m/s with velocity of sound being 340 m/s. The apparent frequency of the sound as heard by the workman A on the track ahead, the driver B on the engine, the guard G in the guard-van and a passenger P in the centre of the train are respectively vA, vB, vC and vD. The values of these apparent frequencies a respectively (in Hz)
(a) vA = 421, vB = 400, vC = 381, vD = 362
(b) vA = 421, vB = 400, vC = 400, vD = 400
(c) vA = 421, vB = 381, vC = 400, vD = 442
(d) vA= 421, vB = 362, vC = 442, vD = 400
Correct Answer is option (b)
(1) Frequency heard by the worker (A) on the track= 421 Hz
(2) Frequency heard by the driver (B) on the train: (The driver travels towards the source with the same speed as the source recedes from him.)= 400 Hz
(3) Frequency heard by the guard on the train. The motion of both the source and the observer and perpendicular to the direction in which sound propagates. Thus the motions have no effect. Hence, frequency heard by the guard = 400 Hz.
(4) Frequency heard by the passenger (P) on the train: Here the source recedes at an angle θ'= 45° and the observer approaches the source at an angle ϕ = 45°. Hence,, since ϕ = 45° being the angles of tangents and a chord of a semicircle. Hence, observed frequency = 400 Hz
Q.3. A longitudinal wave sent by a ship to the bottom of the sea returns after a lapse of 2.64 s. Elasticity of water is 220 kg/mm2 and density of sea water is 1.1 gm/cc. The depth of the sea is (in metres)
(a) 1400
(b) 1848
(c) 924
(d) 700
Correct Answer is option (b)
The velocity of sound in seawater is v == 14 x 102 m/s.
The depth of the well is therefore = 264/2 x 14 x 102 m
= 1848 m
Q.4. A man on the platform is watching two trains, one leaving and the other entering the station with equal speed of 4 m/s. If they sound their whistles each of natural frequency 240 Hz, the number of beats heard by the man (velocity of sound in air = 320 m/s) will be
(a) 6
(b) 3
(c) 0
(d) 12
Correct Answer is option (a)
Apparent frequency of the approaching train is
Apparent frequency of the leaving train is
Hence, the number of beats heard by the man per second
Q.5. An open pipe is suddenly closed at one end with the result that the frequency of third harmonic of the closed pipe is found to be higher by 100 Hz than the fundamental frequency of the open pipe. The fundamental frequency of the open pipe is
(a) 200 Hz
(b) 300 Hz
(c) 240 Hz
(d) 480 Hz
Correct Answer is option (a)
Fundamental frequency of open pipe f0 = v/2
Fundamental frequency of closed pipe
Where, v = velocity of sound in air,
1 = length of pipe.
∴ f0/f0 = 2 ⇒ f0 = 2f'0
By data 3f'0 = f0 + 100 ⇒ 3 x f0/2 = f0 + 100
⇒ 3f'0 = 2f0 + 200 ⇒ f0 = 200Hz
Q.6. A spring is loaded with two blocks m1 and m2 where m1 is rigidly fixed with the spring and m2 is just kept on the block m1 as shown in the figure. The maximum energy of oscillation that is possible for the system having the block m2 in contact with m1 is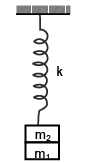
(a) 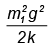
(b) 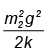
(c) 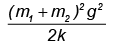
(d) None of these
Correct Answer is option (c)
Let the required amplitude be A. For this amplitude of oscillation the normal contact force between the blocks can be given as m2 g – N = m2 a where a = ω2A
⇒ m2g - N = m2ω2 A
Putting N = 0 for just losing contact for maximum amplitude, we obtain
A = g/ω2 where ω = angular frequency of oscillation of (m1 + m2) and the spring.
Putting ω2= k/m1 + m2, we obtain
Hence, (C) is correct.
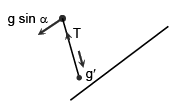
Q.7. The period of oscillation of a simple pendulum of length l suspended from the roof of a vehicle which moves without friction down an inclined plane of inclination α, is given by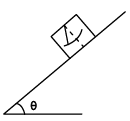 (a)
(a) 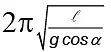
(b) 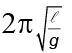
(c) 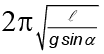
(d) 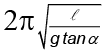
Correct Answer is option (a)
Since the vehicle is moving down the plane with an acceleration g sin a& and the bob moves with same acceleration (because, each and every particle of the system is accelerating with same acceleration down the plane) the string will remain perpendicular to the plane.
⇒ When the bob is released, it moves down perpendicular to the base of the vehicle relative to vehicle with an acceleration= g cos α
⇒ The period of oscillation of the pendulumThe pendulum will oscillate about the mean position that is given by the perpendicular position of the thread to the base of the vehicle.
Hence (A) is correct.
Q.8. One end of a spring of force constant k is fixed to a vertical wall and the other to a block of mass m resting on a smooth horizontal surface. There is another wall at a distance x0 from the block. The spring is then compressed by 2x0 and released. The time taken to strike the wall is
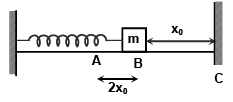 (a)
(a) 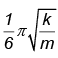
(b) 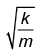
(c) 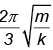
(d) 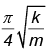
Correct Answer is option (c)
The total time from A to C = tAC = tAB + tBC = (T/4) + tBC
where T = time period of oscillation of spring -mass system
tBC can be obtained from, BC = AB sin (2π/T) tBC putting BC/AB = 1/2 we obtain tBC = T/12
Hence (C) is correct.
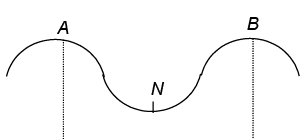
Q.9. A vibrating diaphragm sets up strong vibrations at the mouth of a horizontal tube containing air and a small amount of fine powder. If the powder becomes arranged in piles 1 cm apart, the wavelength of this sound in air is
(a) 1/4cm
(b) 1/2cm
(c) 1 cm
(d) 2 cm
Correct Answer is option (d)
In figure, A, B are antinodes and N is node.
Distance between piles A and B is
λ/2 = 1cm
⇒ λ = 2 cm
Q.10. One end of spring of spring constant k is attached to the centre of a disc of mass m and radius R and the other end of the spring connected to a rigid wall. A string is wrapped on the disc and the end A of the string (as shown in the figure) is pulled through a distance a and then released.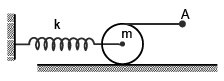 The disc is placed on a horizontal rough surface and there is no slipping at any contact point. What is the amplitude of the oscillation of the centre of the disc?
The disc is placed on a horizontal rough surface and there is no slipping at any contact point. What is the amplitude of the oscillation of the centre of the disc?
(a) a
(b) 2a
(c) a/2
(d) none of these.
Correct Answer is option (c)
Displacement of the topmost point of the disc = a.
Disc undergoes rolling without slipping.
Hence the displacement of the centre of the disc = a/2
Thus amplitude of the oscillation of the centre of the disc = a/2.
Hence, (C) is correct.
Q.11. A disc of radius R and mass M is pivoted at the rim and is set for small oscillations. If simple pendulum has to have the same period as that of the disc, the length of the simple pendulum should be
(a) (5/4) R
(b) (2/3) R
(c) (3/4) R
(d) (3/2) R
Correct Answer is option (d)
Time period of a physical pendulum:. . (A)
Tsimple pendulum =. . . (B)
Equating (A) & (B), l = 3/2 R
Hence, (D) is correct.
Q.12. A particle of mass 10 gm lies in a potential field v = 50 x2 + 100. The value of frequency of oscillations in Hz is
(a) 5 Hz
(b) 5/π Hz
(c) 10/3 Hz
(d) none of these.
Correct Answer is option (b)
v = 50 x2 + 100
dv/dx = 100 x
F = - dv/dx ; F = -100 x; F = -ω2 x
∴ ω = √100 = 10 ; 2πy = 10
y = (10/2π).
Q.13. A uniform spring has a certain block suspended from it and its period for vertical oscillation is T1. The spring is now cut into two parts of lengths 1/3rd and 2/3rd of original length and these springs are connected to the same block as shown in the figure. If time period of oscillation now is T2 then T1/T2.
(a) 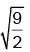
(b) 1: 1
(c) 1: 3
(d) 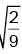
Correct Answer is option (a)
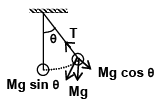
Q.14. A simple pendulum of length L and mass M is oscillating in a plane about a vertical line between angular limits -f and +f. For an angular displacement q(|q| <f) the tension in the string and velocity of the bob are T and v respectively. The following relations hold good under the above condition.
(a) T cosθ = Mg
(b) T + Mg cosθ = Mv2/L
(c) The magnitude of tangential acceleration of the bob | aT | = g sin θ
(d) None of these
Correct Answer is option (c)
T – Mg cosθ = Mv2/L
and | aT | = g sin θ
At maximum angular displacement
T – Mg cosϕ = 0
so T = Mg cosϕ
Hence, The options (C) and (D) are correct.
Q.15. A cylindrical piston of mass M slides smoothly inside a long cylinder closed at one end, enclosing a certain mass of a gas. The cylinder is kept with its axis horizontal. If the piston is slightly compressed isothermally from its equilibrium position, it oscillates simple harmonically, the period of oscillation will be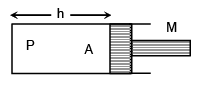 (a)
(a) 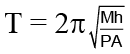
(b) 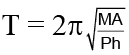
(c) 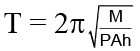
(d) 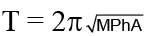
Correct Answer is option (a)
So extra force acting on the piston is given by
α = -ω2 x
Where, w2 = PA/Mh) ⇒ ω =
Q.16. An ideal spring having force constant k is suspended from the rigid support and a block of mass M is attached to its lower end. The mass is released from the natural length of the spring. Then the maximum extension in the spring is
(a) 4Mg/k
(b) 2Mg/k
(c) Mg/k
(d) Mg/2k
Correct Answer is option (b)
Potential energy == mgx ⇒ x = 2Mg/k
Q.17. A uniform spring has certain mass suspended from it and its period for vertical oscillation is T1. The spring is now cut into two parts having the lengths in the ratio of 1 : 2 and same mass is suspended with those two spring as shown in figure. Now time period is T2. The ratio T1 / T2 is
(a) 1
(b) sin θ
(c) 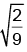
(d) 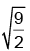
Correct Answer is option (d)
Q.18. A simple pendulum with length L and mass m of the bob is vibrating with an amplitude ‘a’. The tension in the string at the lowest point is
(A) mg
(B) 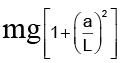
(c) 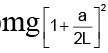
(d) 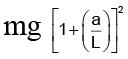
Correct Answer is option (b)
T = mg + mv2/L= mg +
Q.19. A particle executes SHM with an amplitude of 20 cm and time period of 12 sec. The minimum time required for it to move between two points 10 cm on either side of the mean position
(a) 15 s
(b) 2 s
(c) 3 s
(d) 4 s
Correct Answer is option (b)
10 = 20 sin
⇒ t = 1 sec
T = 2t = 2 sec
Q.20. The angular velocity and the amplitude of simple pendulum is ‘ω' and ‘A' respectively. At a displacement 'x' from mean position, if the kinetic energy is T and potential energy is V. Then ratio T to V is
(a) 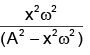
(b) 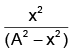
(c) 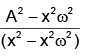
(d) 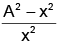
Correct Answer is option (d)
|
446 docs|929 tests
|