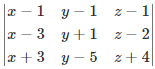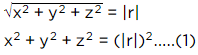JEE Advanced (Single Correct Type): Three dimensional Geometry | Chapter-wise Tests for JEE Main & Advanced PDF Download

Clear all your JEE doubts with EduRev Join for Free

Join for Free

Q.1. Which octant do the point (−5, 4, 3) lie?
(a) Octant I
(b) Octant II
(c) Octant III
(d) Octant IV

Correct Answer is option (b)
Given (−5,4,3) is the point.
Here, the x-coordinate is negative but y and z coordinates are positive. Therefore, (−5,4,3) lie in octant II.

Q.2. The direction cosines of the y-axis are:
(a) (9, 0, 0)
(b) (1, 0, 0)
(c) (0, 1, 0)
(d) (0, 0, 1)

Correct Answer is option (c)
The Direction  cosines of the y-axis are (0, 1, 0)

Q.3. A point is on the x-axis. Which of the following represent the point?
(a) (0, x, 0)
(b) (0, 0, x)
(c) (x, 0, 0)
(d) None of the above

Correct Answer is option (c)
At x-axis, y and z coordinates are zero.

Q.4. Find the equation of the plane passing through the points P(1, 1, 1), Q(3, -1, 2), R(-3, 5, -4).
(a) x + 2y = 0
(b) x – y – 2 = 0
(c) -x + 2y – 2 = 0
(d) x + y – 2 = 0

Correct Answer is option (d)
Given three points, P(1, 1, 1), Q(3, -1, 2) and R(-3, 5, -4).
Equation will be =
On solving we get;
⇒ x + y – 2 = 0

Q.5. Coordinate planes divide the space into ______ octants.
(a) 4
(b) 6
(c) 8
(d) 10

Correct Answer is option (c)
The coordinate planes divide the three dimensional space into eight octants.

Q.6. The equation x² – x – 2 = 0 in three-dimensional space is represented by:
(a) A pair of parallel planes
(b) A pair of straight lines
(c) A pair of the perpendicular plane
(d) None of these

Correct Answer is option (a)
x² −x−2=0⇔(x−2)(x+1)=0
⇔x=2,x=−1 which are the planes (both parallel to YOZ plane).

Q.7. What is the distance between the points (2, –1, 3) and (–2, 1, 3)?
(a) 2√5 units
(b) 25 units
(c) 4√5 units
(d) √5 units

Correct Answer is option (a)
Let the points be P (2, – 1, 3) and Q (– 2, 1, 3)
By using the distance formula,
PQ = √[(x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²]
So here,
x₁ = 2, y₁ = – 1, z₁ = 3
x₂ = – 2, y₂ = 1, z₂ = 3
PQ = √[(-2 – 2)² + (1 – (-1))² + (3 – 3)²]
= √[(-4)² + (2)² + (0)²]
= √[16 + 4 + 0]
= √20
= 2√5
Therefore, the required distance is 2√5 units.

Q.8. The direction ratios of the normal to the plane 7x + 4y – 2z + 5 = 0 are:
(a) 7, 4,-2
(b) 7, 4, 5
(c) 7, 4, 2
(d) 4, -2, 5

Correct Answer is option (a)
The direction ratios of the normal to the plane 7x + 4y – 2z + 5 = 0 are(7, 4, -2)

Q.9. The maximum distance between points (3sin θ, 0, 0) and (4cos θ, 0, 0) is:
(a) 3 units
(b) 4 units
(c) 5 units
(d) Cannot be determined

Correct Answer is option (c)
Let the two points be P (3sin θ, 0, 0) and Q (4cos θ, 0, 0)
Now by distance formula,
PQ = √{(4cos θ – 3sin θ)² + (0 – 0)² + (0 – 0)²}
PQ = √{(4cos θ – 3sin θ)²}
PQ = 4cos θ – 3sin θ
Now, maximum value of 4cos θ – 3sin θ;
= √{(4² + (-3)²}
= √(16 + 9)
= √25
= 5
Thus, PQ = 5 units

So, the maximum distance between points (3sin θ, 0, 0) and (4cos θ, 0, 0) is 5.

Q.10. If l, m, n are the direction cosines of a line, then;
(a) l²+ m²+ 2n² = 1
(b) l²+ 2m²+ n² = 1
(c) 2l²+ m²+ n² = 1
(d) l²+ m²+ n² = 1

Correct Answer is option (d)

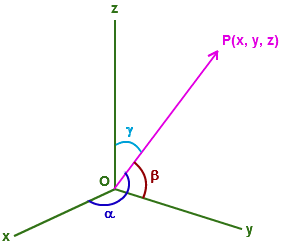
Let vector OP = r, r is the position vector of point P(x, y, z)

And we know that if a line segment of magnitude “r” makes angles α β and γ with x,y and z axes
then x=r cosα,y=r cosβ cosγ are nothing but the direction cosines, which are given as l, m and n, so- x = l.r, y = m.r and z = n.r
So, we’ll have - (using (1))
(l.r)² + (m.r)² + (n.r)² = (|r|)²
or r²(l² + m² + n²) = r²
or l² + m² + n² = 1

Q.11. The locus represented by xy + yz = 0 is:
(a) A pair of perpendicular lines
(b) A pair of parallel lines
(c) A pair of parallel planes
(d) A pair of perpendicular planes

Correct Answer is option (d)
Locus represented by xy + yz = 0
⇒ y(x + z)=0
The planes y = 0 and x + z = 0 are perpendicular

Q.12. Direction ratio of line joining (2, 3, 4) and (−1, −2, 1), are:
(a) (−3, −5, −3)
(b) (−3, 1, −3)
(c) (−1, −5, −3)
(d) (−3, −5, 5)

Correct Answer is option (a)
The direction ratio of the line joining A (2, 3, 4) and B (−1, −2, 1), are:
(−1−2), (−2−3), (1−4)
= (−3, −5, −3)

Q.13. The perpendicular distance of the point P(6, 7, 8) from the XY – Plane is:
(a) 8
(b) 7
(c) 6
(d) None of the above

Correct Answer is option (a)
Let Q be the foot of perpendicular drawn from the point P (6, 7, 8) to the XY plane.
Thus, the distance of this foot Q from P is z-coordinate of P, i.e., 8 units

Q.14. The vector equation for the line passing through the points (–1, 0, 2) and (3, 4, 6) is:
(a) i + 2k + λ(4i + 4j + 4k)
(b) i – 2k + λ(4i + 4j + 4k)
(c) -i+2k+ λ(4i + 4j + 4k)
(d) -i+2k+ λ(4i – 4j – 4k)

Correct Answer is option (c)
The vector equation of the line is given by:
r = a + λ (b – a), λ ∈ R
Let a = -i + 2k
And b = 3i + 4j + 6k
b – a = 4i + 4j + 4k
Let the vector equation be r, then;
r = -i + 2k + λ (4i + 4j + 4k)

Q.15. The image of the point P(1,3,4) in the plane 2x – y + z = 0 is:
(a) (-3, 5, 2)
(b) (3, 5, 2)
(c) (3, -5, 2)
(d) (3, 5, -2)

Correct Answer is option (a)
Let the image of the point P(1, 3, 4) is Q.
The equation of the line through P and normal to the given plane is:
(x – 1)/2 = (y – 3)/-1 = (z – 4)/1
Since the line passes through Q, so let the coordinate of Q are (2k + 1, -k + 3, k + 4)
Now, the coordinate of the mid-point of PQ is:
(k + 1, -k/2 + 3, k/2 + 4)
Now, this midpoint lies in the given plane.
2(k + 1) – (-k/2 + 3) + (k/2 + 4) + 3 = 0
⇒ 2k + 2 + k/2 – 3 + k/2 + 4 + 3 = 0
⇒ 3k + 6 = 0
⇒ k = -2
Hence, the coordinate of Q is (2k + 1, -k + 3, k + 4) = (-4 + 1, 2 + 3, -2 + 4)
= (-3, 5, 2)