JEE Advanced (Subjective Type Questions): Applications of Derivatives - 1 | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q. 1. Prove that the minimum value of  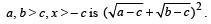             (1979)

Solution. 

Q. 2. Let x and y be two real variables such that x > 0 and xy = 1. Find the minimum value of x+y.            (1981 - 2 Marks)

Ans. 2

Solution. Given that x and y are two real variables such that x > 0 and xy = 1.

To find the minimum value of x + y.

Let S = x + y

Q. 3. For all x in [0, 1], let the second derivative f ¢¢ (x) of a function f(x) exist and satisfy | f '' (x)| < 1. If f (0) = f (1), then show that | f '(x)| < 1 for all  x in [0, 1].    (1981 - 4 Marks)

Solution. We are given that

Here f (x) is continuous on [0, 1], differentiable on (0, 1) and  f (0) = f (1)
∴ By Rolle's thm.,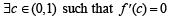
… (1)  
Now there may be three cases for x Î[0,1]
(i) x = c (ii) x > c (iii) x < c

Case I : For x = c.
If x = c then f '(x) = 0<1 [from (1)]
Hence the result | f ' (x) |<1 is obtained in this case.

Case II : For x > c
Consider the interval [c, x].

As f '(x) is continuous on [c, x] and differentiable on (c, x)
∴ | f ' (x) |<1 . Hence the result in this case.

Case III : For x < c Consder the interval [x, c].
As f '(x) is continuous on [x , c] and differentiable on (x, c)

∴ | f "(x) |<1 hence the result in this case.
Combining all the three cases we get

Q. 4. Use the function f (x) =x^{1/ x} , x > 0. to determine the bigger of the two numbers e^π and π^e            (1981 - 4 Marks)

Ans. e^π 

Solution.

⇒ Raising to the power pe on both sides we get

Q. 5. If f(x) and g(x) are differentiable function for 0 < x < 1 such that f(0) = 2, g(0) = 0,  f(1) = 6; g(1) = 2, then show that there exist c satisfying 0< c < 1 and f ' (c) = 2g' (c).           (1982 - 2 Marks)

Solution. Given that f (x) and g (x) are differentiable for x ∈ [0,1] such that  f (0) = 2 ; f (1) = 6,   g (0) = 0 ; g (1) = 2

Let us consider h (x) = f (x) – 2g (x) Then h (x) is continuous on [0, 1] and differentiable on (0, 1)
Also h (0) = f (0) – 2g (0) = 2 – 2 × 0 = 2
h (1) = f (1) – 2g (1) = 6 – 2 × 2 = 2
∴ h (0) = h (1)
∴ All the conditions of Rolle's theorem are satisfied for h(x) on [0, 1]

Q. 6. Find the shortest distance of the point (0, c) from the parabola y = x² where 0 < c < 5.  (1982 - 2 Marks)

Ans. 

Solution. (0, c), y = x², 0 < c < 5 .

Any point on parabola is (x, x²)

Distance between (x, x2) and (0, 1) is

To minimum D we consider

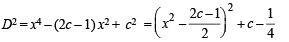
which is minimum when 

Q. 7. for all positive x where a > 0 and b > 0 show that 27ab² > 4c³ .      (1982 - 2 Marks)

Solution. 

To show that 27 ab2 > 4c³ .
Let us consider the function f (x) = ax² + b/x

As a, b are +ve, cubing both sides we get

Q. 8. Show that 1 + x 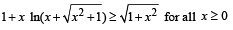                      (1983 - 2 Marks)

Solution. To show

Hence f (x) is increasing function.

Q. 9. Find the coordinates of the point on the curve where the tangent to the curve has the greatest slope.             (1984 - 4 Marks)

Ans. (0, 0)

Solution. Equation of the curve is given by

             ...(1)

Differentiating with respect to x, we get

For the greatest value of slope, we have

Again we find,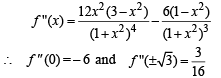

Thus, second order derivative at x = 0 is negative and second order derivative at x =±√3 is positive.

Therefore, the tangent to the curve has maximum slope at (0, 0).

Q. 10. Find all the tangents to the curve y = cos(x + y), - 2p < x < 2π , that are parallel to the line x + 2y = 0.                 (1985 - 5 Marks)

Ans. 2x + 4y - π = 0  

2x + 4y + 3π = 0

Solution. Equation of given curve y = cos (x + y), -2p < x < 2π

Differentiating with respect to x

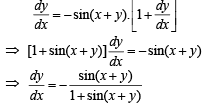                                ...(1)

Since the tangent to given curve is parallel to x + 2y = 0

⇒ 2sin (x + y) = 1 + sin (x + y)
⇒ sin (x + y) = 1
Thus, cos (x + y) = 0
Using equation of curve and above result, we get, y = 0

Thus the points on curve at which tangets are parallel to given line are (π/2, 0) and (– 3π/2, 0)

The equation of tangent at (π/2, 0) is

Thus the required equations of tangents are

Q. 11. Find the intervals in which λ should lie in order that f(x) has exactly one minimum and exactly one maximum.         (1985 - 5 Marks)

Ans. 

Solution. The given function is,

f (x) = sin³ x + λ sin² x for – π/2 <  x  < π/2

∴ f ' (x) = 3 sin² x cos x + 2λ sin x cos x

So, from f ' (x) = 0, we get x = 0 or 3 sin x + 2λ = 0

f " (x) = 3 sin x cos2 x = – 2λ cos2 x

Now, if 0  < x < π/2, then – 3/2 < λ < 0 and therefore f " (x) > 0.
⇒ f (x) has one minimum for this value of λ.

Also for x = 0, we have f " (0) = 2λ < 0, That is f (x) has a maximum at x = 0

Again if – p/2 < x < 0, then 0 <  λ <  3/2 and therefore f " (x) = – 2λ cos2 x < 0.

So that f (x) has a maximum.

Also for x = 0, f " (a) = 2λ > 0 so that f (x) has a minimum.

Thus, for exactly one maximum and minimum value of f (x),λ must lie in the interval

Q. 12. Find the point on the curve 4x² + a² y² = 4a², 4 < a² < 8 that is farthest from the point (0, – 2).                (1987 - 4 Marks)

Ans. (0, 2)

Solution. The equation of given curve can be expressed as

Clearly it is the question of an ellipse

Let us consider a point P (a cos θ, 2 sin θ) on the ellipse.

Let the distance of P (a cos θ, 2 sin θ) from (0, – 2) is L.

Then, L² = (a cos θ – 0)2 + (2 sin θ + 2)²

⇒ Differentiating with respect to θ, we have

For max. or min. value of L we should have

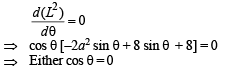
∴ L is max. at θ = π/2 and the farthest point is (0, 2).

Q. 13. Investigate for maxima and minima the function 

Ans. f is min at x = 7/5

Solution. We have,

Then using the theorem, 

We get, 

For extreme values f ' (x) = 0 ⇒ x = 1, 2, 7/5
Now, f " (x) = (x – 2)² (5x – 7) + 2 (x – 1) (x – 2) (5x – 7) + 5 (x – 1) (x – 2)²
At x = 1,  f " (x) = 1 (– 2) = – 2 < 0
∴ f is max. at x = 1
At  x = 2 f " (x) = 0
∴ f is neither maximum nor minimum at x = 2.

Q. 14. Find all maxima and minima of the function y = x( x - 1)² , 0 < x < 2     (1989 - 5 Marks)

Ans. 

Solution. 

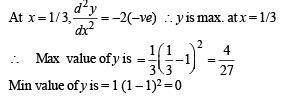
Now the curve cuts the axis x at (0, 0) and (1, 0). When x increases from 1 to 2, y also increases and is +ve.
When y = 2, x (x – 1)² = 2
⇒ x = 2
Using max./min. values of y and points of intersection with x-axis, we get the curve as in figure and shaded area is the required area.
∴ The required area = Area of square 

Q. 15. Show that 2sin x + tan x >3x                 (1990 -  4 Marks)

Solution. Let f (x) = 2 sin x + tan x – 3x on 0 < x < π /2

then f ' (x) = 2 cos x + sec² x – 3 and f " (x)

= – 2 sin x + 2 sec2 x tan x  

= 2 sin x [sec³ x – 1]

⇒ f ' (x) is an increasing function on 0 < x <π / 2.

⇒ f (x) is an increasing function on

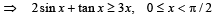  Hence proved

Q. 16. A point P is given on the circumference of a circle of radius r. Chord QR is parallel to the tangent at P. Determine the maximum possible area of the triangle PQR.     (1990 -  4 Marks)

Ans. 

Solution. As QR || XY diameter through P is ⊥ QR. 

Now area of ΔPQR is given by 

But QR = 2.QA = 2r sin 2θ and PA = OA + OP = r cos 2θ + r

= r². 2 sin θ cos θ . 2 cos² θ = 4 r² sin q cos³ θ

∴ A is maximum at q = 30°

Q. 17. A window of perimeter P (including the base of the arch) is in the form of a rectangle surmounded by a semi circle. The semi- circular portion is fitted with coloured glass while the rectangular part is fitted with clear glass transmits three times as much light per square meter as the coloured glass does.

What is the ratio for the sides of the rectangle so that the window transmits the maximum light ? (1991 -  4 Marks)

Ans. 6 + π : 6

Solution. Let ABCEDA be the window as shown in the figure and let 

AB = x m
 BC = y m

Then its perimeter including the base DC of arch

            ...(1)

Now, area of rectangle ABCD = xy

and  area of arch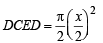 

Let λ be the light transmitted by coloured glass per sq. m. Then 3λ will be the light transmitted by clear glass per sq. m.

Hence the area of light transmitted 

          ...... (2)

Substituting the value of y from (1) in (2), we get

For A to be maximum 

[Using value of P from (1)]

∴The required ratio of breadth to length of the rectangle

= 6 + π : 6

Q. 18. A cubic f (x) vanishes at x = 2 and has relative minimum / maximum at   cubic f(x).    (1992 - 4 Marks)

Ans. x³ + x² -x+ 2

Solution. Let f (x) = ax³ + bx² + cx + d

ATQ, f (x) vanishes at x = – 2

⇒ – 8a + 4b – 2c + d = 0     ...(1)

f ' (x) = 3ax2 + 2bx + c

Againg ATQ, f (x)  has relative max./min at

⇒ f ' (– 1) = 0 = f ' (1/3)

⇒ 3a – 2b + c = 0           ... (2)

and a + 2b + 3c = 0          ... (3)

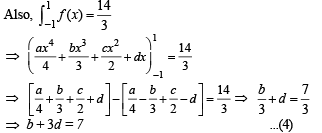
⇒ b + 3d = 7            ...(4)

From (1), (2), (3), (4) on solving, we get

a = 1, b = 1, c = – 1, d = 2

∴ The required cubic is x³ + x2 – x + 2.

Q. 19. What normal to the curve y = x² forms the shortest chord?    (1992 - 6 Marks)

Ans. 

Solution. The given curve is y = x² ...(1)

Consider any point A (t, t²) on (1) at which normal chord drawn is shortest.

Then eq. of normal to (1) at A (t, t²) is

            ...(2)

This normal meets the curve again at point B which can be obtained by solving (1) and (2) as follows :

Putting y = x² in (2), we get

For shortest chord, we have to minimize Z, and for that dZ/dt =0 

Q. 20. Find the equation of the normal to the curve y = (1 + x)^y+ sin ^-1 (sin²x) at x = 0         (1993 - 3 Marks)

Ans. x +y = 1

Solution. The given curve is y = (1+ x)^y + sin^–1 (sin² x)

Here at x = 0, y = (1 + 0)y + sin^–1 (0) ⇒ y = 1

∴  Point at which normal has been drawn is (0, 1).

For slope of normal we need to find dy/dx, and for that we consider the curve as 

∴ Equation of normal to given curve at (0, 1) is

Q. 21. 

Find all possible real values of b such that f(x) has the smallest value at x = 1.   (1993 - 5 Marks)

Ans. b ∈ (-2, - 1) ∪ (1,∞)

Solution. 

We can see from definition of the function, that

f (1) = 2(1) – 3 = – 1

Also f (x) is increasing on [1, 3], f ' (x) being 2 > 0.
∴ f (1) = – 1 is the smallest value of f (x)
Again f ' (x) = – 3x² for x ∈ [0, 1] such that f ' (x) < 0
⇒ f (x) is decreasing on [0, 1]
∴ For fixed value of b, its smallest occur when x → 1

As given that the smallest value of f (x) occur at x = 1
∴ Any other smallest value > f (1)

⇒ b ∈ (-2, - 1) ∪ (1,∞)