JEE Advanced (Subjective Type Questions): Conic Sections | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. Suppose that the normals drawn at three different points on the parabola y2 = 4x pass through the point (h, k). Show that h > 2. (1981 - 4 Marks)
Ans. 2
Sol. The equation of a normal to the parabola y2 = 4ax in its slope form is given by
y = mx – 2am – am3
∴Eq. of normal to y2 = 4x, is y = mx – 2m – m3 ...(1)
Since the normal drawn at three different points on the parabola pass through (h, k), it must satisfy the equation (1)
∴k = mh – 2m – m3 ⇒ m3 – (h – 2) m + k = 0
This cubic eq. in m has three different roots say m1, m2, m3
∴m1 + m2 + m3 = 0 ...(2)
m1m2 + m2m3 + m3m1 = – (h – 2) ...(3)
Now, (m1 + m2 + m3)2 = 0 [Squaring (2)]
⇒ m12 + m22+m32 = – 2 (m1m2 + m2m3 + m3m1) ⇒ m12 + m22 + m32 = 2 (h – 2) [Using (3)]
Since LHS of this equation is he sum of perfect squares, therefore it is + ve
∴h – 2 > 0 ⇒ h > 2 Proved
Q.2. A is a point on the parabola y2 = 4ax. The normal at A cuts the parabola again at point B. If AB subtends a right angle at the vertex of the parabola. find the slope of AB. (1982 - 5 Marks)
Ans. m =± 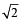
Sol. Parabola y2 = 4ax.
Let at any pt A equation of normal is y = mx – 2am – am3. ...(1)
Combined equation of OA and OB can be obtained by making equation of parabola homogeneous with the help of normal.
∴Combined eq. of OA and OB is
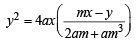
[ From eqn. (1) using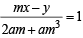 ]
]
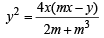
⇒ 4mx2 – 4xy – (2m + m3) y2 = 0 But angle between the lines represented by this pair is 90°.
⇒ coeff. of x2 + coeff of y2 = 0 ⇒ 4m – 2m – m3 = 0
⇒ m3 – 2m = 0 ⇒ m = 0, 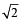 , –
, –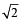
But for m = 0 eq. of normal becomes y = 0 which does not intersect the parabola at any other point.
∴ m =± 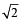
Q.3. Three normals are drawn from the point (c, 0) to the curve y2 = x. Show that c must be greater than 1/2. One normal is always the x-axis. Find c for which the other two normals are perpendicular to each other. (1991 - 4 Marks)
Ans. c = 3/4
Sol. Given parabola is y2 = x.
Normal is y = 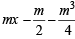
As per question this normal passes through (c, 0) therefore, we get
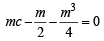 ...(1)
...(1)
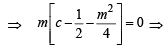
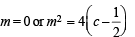
m = 0 shows normal is y = 0 i.e. x-axis is always a normal.
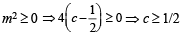
At c = 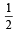 from (1) m = 0
from (1) m = 0
∴for other real values of m, c > 1/2
Now for other two normals to be perpendicular to each other, we must have m1.m2 = – 1
Or in other words, if m1,m2 are roots of 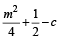 = 0, then product of roots = – 1
= 0, then product of roots = – 1
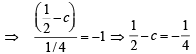 ⇒ c = 3/4
⇒ c = 3/4
Q.4. Through the vertex O of parabola y2 = 4x, chords OP and OQ are drawn at right angles to one another. Show that for all positions of P, PQ cuts the axis of the parabola at a fixed point. Also find the locus of the middle point of PQ. (1994 - 4 Marks)
Ans. y2 = 2 (x – 4)
Sol. Let the equation of chord OP be y = mx.
Then eqn of chord OQ will be  [∵ OQ ⊥ OP]
[∵ OQ ⊥ OP]
P is pt. of intersection of y = mx and y2 = 4x.
Solving the two we get 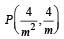
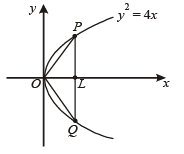
Q is pt. of intersection of 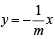 and y2 = 4x.
and y2 = 4x.
Solving the two we get Q (4m2, – 4m)
Now eq. of PQ is
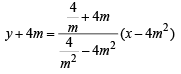
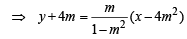
⇒ (1 – m2) y + 4m – 4m3 = mx – 4m3 ⇒ mx – (1 – m2) y – 4m = 0
This line meets x-axis where y = 0 i.e. x = 4
⇒ OL = 4, which is constant as independent of m. Again let (h, k) be the mid pt. of PQ, then
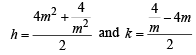
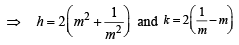
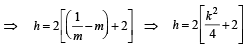
⇒ 2h = k2 + 8 ⇒ k2 = 2 (h – 4)
∴ Locus of (h, k) is y2 = 2 (x – 4)
Q.5. Show that the locus of a point that divides a chord of slope 2 of the parabola y2 = 4x internally in the ratio 1: 2 is a parabola. Find the vertex of this parabola. (1995 - 5 Marks)
Ans. (2/9, 8/9)
Sol. Let P (t12 , 2t1) and Q (t22 , 2t2) be the ends of the chord PQ of the parabola
y2 = 4x ...(1)
∴Slope of chord PQ 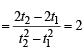
⇒ t2 + t1 = 1 ...(2)
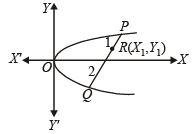
If R(x1, y1) is a point dividing PQ internally in the ratio 1 : 2, then
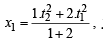
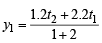
⇒ t22 + 2t12 =3x1 ...(3)
and t2 + 2t1= (3y1) /2 ...(4)
From (2) and (4), we get
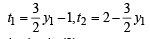
Substituting in (3), we get
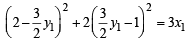
⇒ (9/4)y12 – 4y1 =x1-2

∴Locus of the point R ( x1 ,y1) is (y – 8/9)2 = (4/9) (x – 2/9) which is a parabola having vertex at the point (2/9, 8/9).
Q.6. Let ‘d’ be the perpendicular distance from the centre of the ellipse 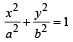 to the tangent drawn at a point P on the ellipse. If F1 and F2 are the two foci of the ellipse, then show that
to the tangent drawn at a point P on the ellipse. If F1 and F2 are the two foci of the ellipse, then show that 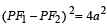
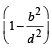 (1995 - 5 Marks)
(1995 - 5 Marks)
Ans.
Sol. Equation to the tangent at the point P (a cosθ, b sinθ) on x2/a2 + y2/b2 = 1 is
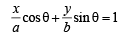 ...(1)
...(1)
∴d = perpendicular distance of (1) from the centre (0, 0) of the ellipse
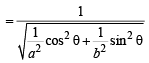
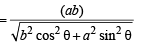
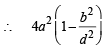 =
= 
= 4 (a2 – b2) cos2θ = 4a2 e2 cos2θ....(2)
The coordinates of focii F1 and F2 are F1 = (ae, 0) and F2 = (–ae, 0)
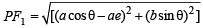
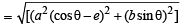
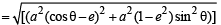
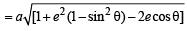
= a (1 – e cosθ) Similarly, PF2 = a (1 + e cosθ)
∴(PF1 – PF2)2 = 4a2 e2 cos2θ ...(3)
Hence from (2) and (3), we have
(PF1 – PF2)2 = 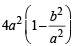
Q.7. Points A, B and C lie on the parabola y2 = 4ax. The tangents to the parabola at A, B and C, taken in pairs, intersect at points P, Q and R. Determine the ratio of the areas of the triangles ABC and PQR. (1996 - 3 Marks)
Ans. 2 : 1
Sol. Let the three points on the parabola y2 = 4ax be A (at12 , 2at1) , B(at22 , 2at2) and C (at32 , 2at3) .
Then using the fact that equation of tangent to y2 = 4ax at (at2, 2at) is 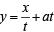 , we get equations of tangents at A, B and C as folllows
, we get equations of tangents at A, B and C as folllows
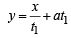 ...(1)
...(1)
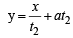 ...(2)
...(2)
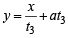 ...(3)
...(3)
Solving the above equations pair wise we get the pts.
P (at1t2, a (t1 + t2))
Q (at2t3, a (t2 + t3))
R (at3t1, a (t3 + t1))
Now, area of ΔABC =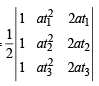
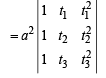
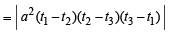 ...(4)
...(4)
Also area of ΔPQR 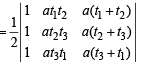
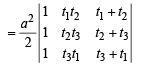
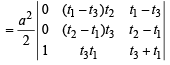
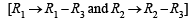
Expanding along C1,
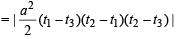
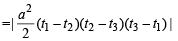 ...(5)
...(5)
From equations (4) and (5), we get
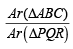
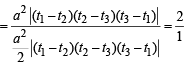
∴The required ratio is 2 : 1
Q.8. From a point A common tangents are drawn to the circle x2 + y2 = a2/2 and parabola y2 = 4ax. Find the area of the quadrilateral formed by the common tangents, the chord of contact of the circle and the chord of contact of the parabola. (1996 - 2 Marks)
Ans.
Sol. This line will touch the circle x2 + y2 = a2/2
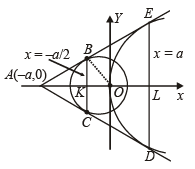
if 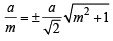
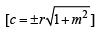
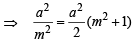
⇒ 2 = m4 + m2 ⇒ m4 + m2 – 2 = 0
⇒ (m2 + 2) (m2 – 1) = 0 ⇒ m = 1, – 1
Thus the two tangents (common one) are y = x + a and y = – x – a
These two intersect each other at (– a, 0) The chord of contact at A (– a, 0) for the circle x2 + y2 = a2/2 is
(– a. x) + 0.y = a2/2 i.e., x = – a/2 and the chord of contact at A (– a,0) for the parabola y2 = 4ax is 0.y = 2a (x – a) i.e., x = a
Note that DE is latus recturn of parabola y2 = 4ax, therefore its lengths is 4a.
Chords of contact are clearly parallel to each other, so req. quadrilateral is a trapezium.
Ar (trap BCDE) 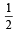 = BC + DEx KL
= BC + DEx KL
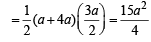
Q.9. A tangent to the ellipse x2 + 4y2 = 4 meets the ellipse x2 + 2y2 = 6 at P and Q. Prove that the tangents at P and Q of the ellipse x2 + 2y2 = 6 are at right angles.(1997 - 5 Marks)
Ans.
Sol. The given ellipses are
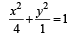 ...(1)
...(1)
and 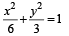 ...(2)
...(2)
Then the equation of tangent to (1) at any point T (2 cosθ, sinθ) is given by

or 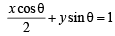 ...(3)
...(3)
Let this tangent meet the ellipse (2) at P and Q.
Let the tangents drawn to ellipse (2) at P and Q meet each other at R (x1, y1)
Then PQ is chord of contact of ellipse (2) with respect to the pt R (x1, y1) and is given by
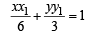 ...(4)
...(4)
Clearly equations (3) and (4) represent the same lines and hence should be identical. Therefore comparing the cofficients, we get
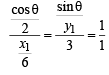
⇒ x1 = 3 cosθ , y1 = 3 sinθ ⇒ x12 +y12= 9
⇒ Locus of (x1, y1) is x2 + y2 = 9
which is the director circle of the ellipse 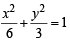 = and
= and
Thus tangents at P and Q are at right ∠’s.
KEY CONCEPT : We know that the director circle is the locus of intersection point of the tangents which are at right ∠.
Q.10. The angle between a pair of tangents drawn from a point P to the parabola y2 =4ax is 45°. Show that the locus of the point P is a hyperbola. (1998 - 8 Marks)
Ans.
Sol. Let P (e, f) be any point on the locus. Equation of pair of tangents from P (e, f) to the parabola y2 = 4ax is [ fy – 2a (x + e)]2
= (f 2 – 4ae) (y2 – 4ax) [T2 = SS1]
Here, a = coefficient of x2 = 4a2 ...(1)
2h = coefficient of xy = – 4af ...(2)
and b = coefficient of y2 = f 2 – (f 2 – 4ae) = 4ae ...(3)
If they include an angle 45°, then
1 tan 45°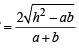
or,(a + b)2 = 4 (h2 – ab)
or, (4a2 + 4ae)2 = 4 [4a2f 2 – (4a2) (4ae)]
or,(a + e)2 = f2 – 4ae or e2 + 6ae + a2 – f2 = 0
or(e + 3a)2 – f 2 = 8a2
Hence the required locus is (x + 3a)2 – y2 = 8a2, which is a hyperbola.
Q.11. Consider the family of circles x2 + y2 = r2, 2 < r < 5. If in the first quadrant, the common taingent to a circle of this family and the ellipse 4x2 + 25y2 = 100 meets the co-ordinate axes at A and B, then find the equation of the locus of the mid-point of AB. (1999 - 10 Marks)
Ans. Sol. Let any point P on ellipse 4x2 + 25y2 = 100 be (5 cosθ, 2 sinθ). So equation of tangent to the ellipse at P will be
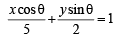
Tangent (1) also touches the circle x2 + y2 = r2, so its distance from origin must be r.
Tangent (2) intersects the coordinate axes at 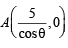 and
and 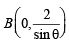 respectively. Let M (h, k) be the midpoint of line segment AB. Then by mid point formula
respectively. Let M (h, k) be the midpoint of line segment AB. Then by mid point formula
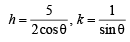 ⇒
⇒ 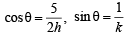
⇒ 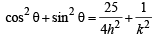
Hence locus of M (h, k) is 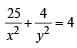
Locus is independent of r.
Q.12. Find the co-ordinates of all the points P on the ellipse 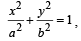 , for which the area of the triangle PON is maximum, where O denotes the origin and N, the foot of the perpendicular from O to the tangent at P.(1999 - 10 Marks)
, for which the area of the triangle PON is maximum, where O denotes the origin and N, the foot of the perpendicular from O to the tangent at P.(1999 - 10 Marks)
Ans.
Sol. The ellipse is 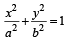 ..(1)
..(1)
Since this ellipse is symmetrical in all four quadrants, either there exists no such P or four points, one in each qudrant.
Without loss of generality we can assume that a > b and P lies in first quadrant.
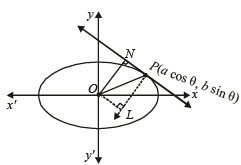
Let P (a cosθ, b sinθ) then equation of tangent is
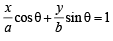
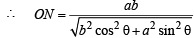
Equation of ON is 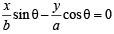
Equation of normal at P is ax secθ – by cosecθ = a–2 b2

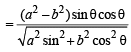
and NP = OL
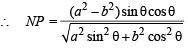
∴Z = Area of OPN =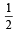 x ON x NP
x ON x NP
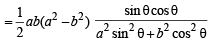
Let u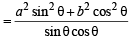 = a2 tanθ + b2 cotθ
= a2 tanθ + b2 cotθ
 ⇒ tanθ = b/a
⇒ tanθ = b/a
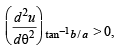 u is minimum at θ = tan–1 b/a
u is minimum at θ = tan–1 b/a
So Z is maximum at θ = tan–1 b/a
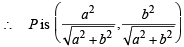
By symmetry, we have four such points
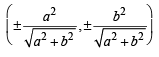
Q.13. Let ABC be an equilateral triangle inscribed in the circle x2 + y2 = a2. Suppose perpendiculars from A, B, C to the major axis of the ellipse
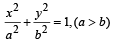 meets the ellipse respectively, at P, Q, R. so that P, Q, R lie on the same side of the major axis as A, B, C respectively. Prove that the normals to the ellipse drawn at the points P, Q and R are concurrent. (2000 - 7 Marks)
meets the ellipse respectively, at P, Q, R. so that P, Q, R lie on the same side of the major axis as A, B, C respectively. Prove that the normals to the ellipse drawn at the points P, Q and R are concurrent. (2000 - 7 Marks)
Ans.
Sol. Let A, B, C be the point on circle whose coordinates are A = [a cosθ , a sinθ ]
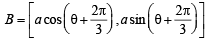
and 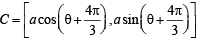
Further, P [ a cosθ , b sinθ ] (Given)
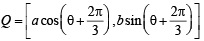
and 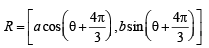
It is given that P, Q, R are on the same side of x-axis as A, B, C.
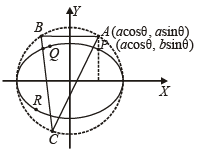
So required normals to the ellipse are ax secθ– by cosecθ= a2 – b2 ...(1)
 ...(2)
...(2)
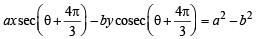 ...(3)
...(3)
Now, above three normals are concurrent ⇒ Δ = 0
where Δ 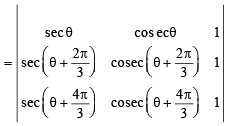
Multiplying and dividing the different rows R1, R2 and R3 by sinθ cosθ ,
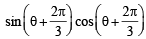
and 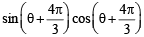 respectively, we get
respectively, we get
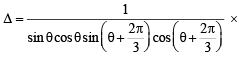
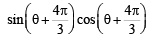
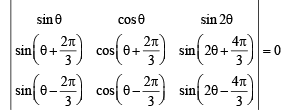
[Operating R2 → R2 + R3 and simplyfing R2 we get R2 ≡ R1]
Q.14. Let C1 and C2 be respectively, the parabolas x2 = y – 1 and y2 = x – 1. Let P be any point on C1 and Q be any point on C2. Let P1 and Q1 be the reflections of P and Q, respectively, with respect to the line y = x. Prove that P1 lies on C2, Q1 lies on C1 an d PQ ≥ min{PP1, QQ1} . Hence or otherwise determine points P0 and Q0 on the parabolas C1 and C2 respectively such that P0Q0 ≤ PQ for all pairs of points (P,Q) with P on C1 and Q on C2. (2000 - 10 Marks)
Ans. Sol. Given that C1 : x2 = y – 1 ; C2 : y2 = x – 1
Let P ( x1 ,x12 + 1) on C1 and Q ( y22 + 1,y2) on C2.
Now the reflection of pt P in the line y = x can be obtained by interchanging the values of abscissa and ordiante.
Thus reflection of pt. P ( x1,x12 + 1) is P1 ( x12 + 1,x1) and reflection of pt. Q ( y22 + 1,y2) is Q1 ( y2 ,y22 + 1)
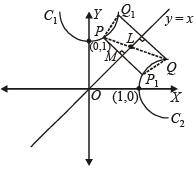
It can be seen clearly that P1 lies on C2 and Q1 on C1.
Now PP1 and QQ1 both are perpendicular to mirror line y = x.
Also M is mid pt. of PP1 (Q P1 is morror image of P in y = x)
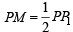
In rt ΔPML,
PL > PM ⇒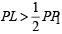 ..(i)
..(i)
Similarly,
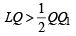 ...(ii)
...(ii)
Adding (i) and (ii) we get
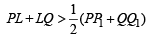
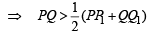
⇒ PQ is more than the mean of PP1 and QQ1
⇒ PQ ≥ min (PP1, QQ1) Let min (PP1, QQ1) = PP1
then 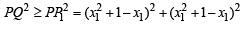
= 2(x12 + 1 – x1)2 = f (x1)
⇒ f '( x1) = 4(x12 + 1 – x1)(2x1 – 1)
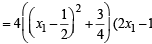
∴f ' (x1) = 0 when x1 = 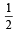
Also f ' (x1) < 0 if x1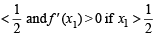
⇒ f (x1) is min when x1 = 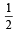
Thus if at x1 = 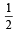 pt P is P0 on C1
pt P is P0 on C1
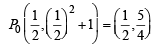
Similarly Q0 on C2 will be image of P0 with respect to y = x
∴ 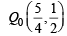
Q.15. Let P be a point on the ellipse 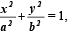 0 < b < a. Let the line parallel to y-axis passing through P meet the circle x2 + y2 = a2 at the point Q such that P and Q are on the same side of x-axis. For two positive real numbers r and s, find the locus of the point R on PQ such that PR : RQ = r : s as P varies over the ellipse. (2001 - 4 Marks)
0 < b < a. Let the line parallel to y-axis passing through P meet the circle x2 + y2 = a2 at the point Q such that P and Q are on the same side of x-axis. For two positive real numbers r and s, find the locus of the point R on PQ such that PR : RQ = r : s as P varies over the ellipse. (2001 - 4 Marks)
Ans.
Sol. Let the co-ordinates of P be (a cosθ , b sinθ ) then coordinates of Q are (a cosθ , a sinθ )

As R (h, k) divides PQ in the ratio r : s, then
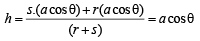
⇒
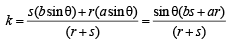
⇒ 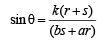 ∵ cos2θ + sin2θ = 1
∵ cos2θ + sin2θ = 1
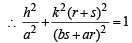
Hence locus of R is 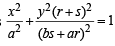 which is equation of an ellipse.
which is equation of an ellipse.
Q.16. Prove that, in an ellipse, the perpendicular from a focus upon any tangent and the line joining the centre of the ellipse to the point of contact meet on the corresponding directrix. (2002 - 5 Marks)
Ans. Sol.
Let the ellipse be 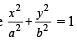 and O be the centre.
and O be the centre.
Tangent at P (x1, y1) is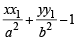 = 0 whose
= 0 whose
slope = 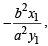 Focus is S (ae, 0).
Focus is S (ae, 0).
Equation of the line perpendicular to tangent at P is
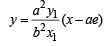 ....(1)
....(1)
Equation of OP is 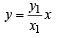 ...(2)
...(2)
(1) and (2) intersect 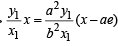
⇒ x (a2 – b2) = a3e ⇒ x. a2e2 = a3e
⇒ x = a/e
Which is the corresponding directrix.
Q.17. Normals are drawn from the point P with slopes m1, m2, m3 to the parabola y2 = 4x. If locus of P with m1 m2 = a is a part of the parabola itself then find a. (2003 - 4 Marks)
Ans. α = 2
Sol. Let P be the pt. (h, k). Then eqn of normal to parabola y2 = 4x from point (h, k), if m is the slope of normal, is y = mx – 2m – m3
As it passes through (h, k), therefore mh – k – 2m – m3 = 0 or, m3 + (2 – h) + k = 0 ...(1)
Whcih is cubic in m, giving three values of m say m1, m2 and m3.
Then m1m2m3 = – k (from eqn) but given that m1m2 = a
∴We get m3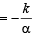
But m3 must satisfy eqn (1)
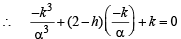
⇒ k2 – 2α2 – hα2 – α3 = 0
∴Locus of P (h, k) is y2 = α2x + (α3 – 2α2)
But ATQ, locus of P is a part of parabola y2 = 4x, therefore comparing the two, we get α2 = 4 and α3 – 2α2 = 0 ⇒ α = 2
Q.18. Tangent is drawn to parabola y2 – 2y – 4x + 5 = 0 at a point P which cuts the directrix at the point Q. A point R is such that it divides QP externally in the ratio 1/2 : 1. Find the locus of point R. (2004 - 4 Marks)
Ans. ( x - 1)(y - 1)2 + 4=0
Sol. The given eqn of parabola is y2 – 2y – 4x + 5 = 0 ...(1)
⇒ (y – 1)2 = 4 (x – 1)
Any parametric point on this parabola is P (t2 + 1, 2t + 1)
Differentiating (1) w.r. to x, we get

∴Slope of tangent to (1) at point P (t2 + 1, 2t + 1) is
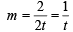
∴Eqn of tangent at P (t2 + 1, 2t + 1) is
y – (2t + 1)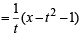
⇒ yt – 2t2 – t = x – t2 = 1
⇒ x – yt + (t2 + t – 1) = 0 ...(2)
Now directrix of given parabola is (x – 1) = – 1 ⇒ x = 0
Tangent (2) meets directix at 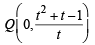
Let pt. R be (h, k)
ATQ, R divides the line joing QP in the ratio 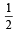 :1 i.e., 1 : 2
:1 i.e., 1 : 2
externally.
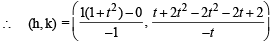
⇒ h = – (1 + t2) and 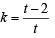
⇒ t2 = – 1 – h and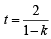
Eliminating t, we get 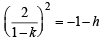
⇒ 4 = – (1 – k)2 (1 – h) ⇒ (h – 1) (k – 1)2 + 4 = 0
∴Locus of R (h, k) is (x – 1) (y – 1)2 + 4 = 0
Q.19. Tangents are drawn from any point on the hyperbola
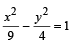 to the circle x2 + y2 = 9. Find the locus of mid-point of the chord of contact. (2005 - 4 Marks)
to the circle x2 + y2 = 9. Find the locus of mid-point of the chord of contact. (2005 - 4 Marks)
Ans.
Sol. Any pt on the hyperbola 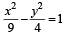 is (3 secθ , 2 tanθ) Then, equation of chord of contact to the circle x2 + y2 = 9,
is (3 secθ , 2 tanθ) Then, equation of chord of contact to the circle x2 + y2 = 9,
with respect to the pt. (3 secθ, 2 tanθ) is (3 secθ) x + (2 tanθ) y = 9 ...(i)
If (h, k) be the mid point of chord of contact then equation of chord of contact will be hx + ky – 9 = h2 + k2 – 9 (T = S1)
or, hx + ky = h2 + k2 ...(ii)
But equations (i) and (ii) represent the same st. line and hence should be identical, therefore, we get
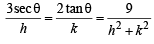

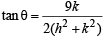
sec2θ – tan2θ = 1
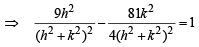


∴Locus of (h, k) is 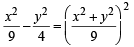
Q.20. Find the equation of the common tangent in 1st quadrant to the circle x2 + y2 = 16 and the ellipse
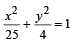 Also find the length of the intercept of the tangent between the coordinate axes. (2005 - 4 Marks)
Also find the length of the intercept of the tangent between the coordinate axes. (2005 - 4 Marks)
Ans.
Sol. Let the common tangent to circle x2 + y2 = 16 and ellipse x2/25 + y2 /4 = 1 be
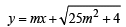 ..(i)
..(i)
As it is tangent to circle x2 + y2 = 16, we should have
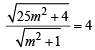
[Using : length of perpendicular from (0,0 ) to (1) = 4]
⇒ 25m2 + 4 = 16m2 + 16 ⇒ 9m2 =12
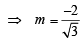
[Leaving + ve sign to consider tangent in I quadrant] ∴Equation of common tangent is
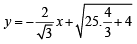
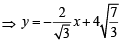
This tangent meets the axes at 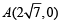 and
and
∴Length of intercepted portion of tangent between axes
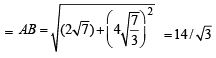
|
481 docs|964 tests
|
















