JEE Advanced (Subjective Type Questions): Definite Integrals & Applications of Integrals - 1 | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q. 1. Find the area bounded by the curve x2 = 4y and the straight line x = 4y – 2. (1981 - 4 Marks)
Ans. 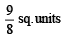
Solution. To find the area bounded by
x2 = 4y ..(1)
which is an upward parabola with vertex at (0, 0).
which is a st. line with its intercepts as –2 and 1/2 on axes. For Pt’s of intersection of (1) and (2) putting value of 4y fom (2) in (1) we get
x2 = x+2 ⇒ x2 -x -2 = 0 ⇒ (x-2)(x+1) = 0
⇒ x = 2,-1 ⇒ y = 1,1 /4
∴ A(-1,1 / 4)B(2,1).
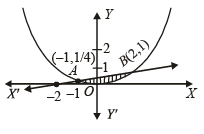
Shaded region in the fig is the req area.
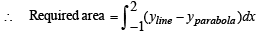
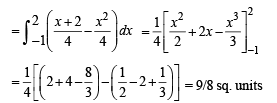
Q. 2. Show that : 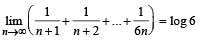 (1981 - 2 Marks)
(1981 - 2 Marks)
Solution. We know that in integration as a limit sum
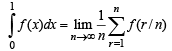
Similarly the given series can be written as
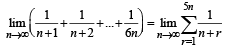
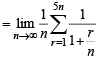
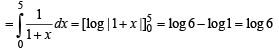
Q. 3. 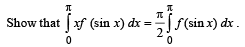 (1982 - 2 Marks)
(1982 - 2 Marks)
Solution. 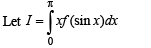 … (1)
… (1)
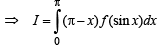
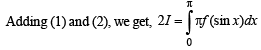
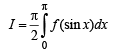 Hence Proved.
Hence Proved.
Q. 4. 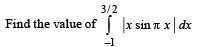 (1982 - 3 Marks)
(1982 - 3 Marks)
Ans. 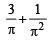
Solution.
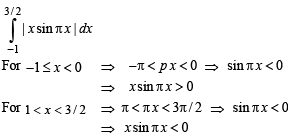
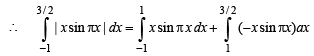
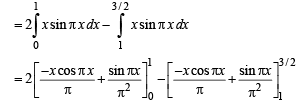
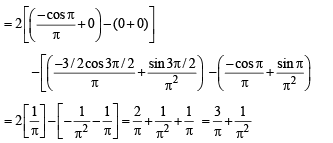
Q. 5. 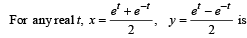 is a point on the hyperbola x2 – y2 = 1. Show that the area bounded by this hyperbola and the lines joining its centre to the points corresponding to t1 and –t1 is t1. (1982 - 3 Marks)
is a point on the hyperbola x2 – y2 = 1. Show that the area bounded by this hyperbola and the lines joining its centre to the points corresponding to t1 and –t1 is t1. (1982 - 3 Marks)
Solution. Let P(t1) and Q(–t1) be two points on the hyperbola.
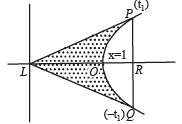
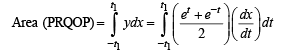
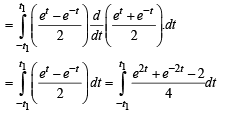
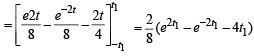
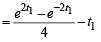
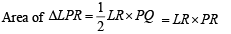
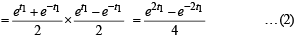
∴ The required area = Ar (ΔLPQ)- Ar ( PRQOP)
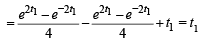
Q. 6. 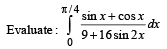 (1983 - 3 Marks)
(1983 - 3 Marks)
Ans. 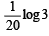
Solution.
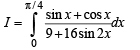
Let sin x - cox x = t ⇒ as x → 0,t →-1 as x → π / 4,t → 0
⇒ (cos x + sin x)dx= dt
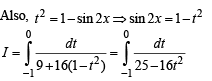
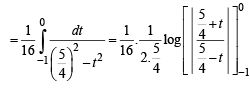
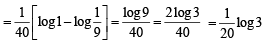
Q. 7. Find the area bounded by the x-axis, part of the curve 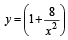 and the ordinates at x = 2 and x = 4. If the ordinate at x = a divides the area into two equal parts, find a. (1983 - 3 Marks)
and the ordinates at x = 2 and x = 4. If the ordinate at x = a divides the area into two equal parts, find a. (1983 - 3 Marks)
Ans. a = 2√2
Solution.
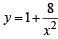
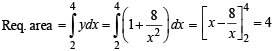
If x = 4a bisects the area then we have
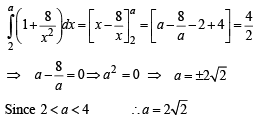
Q. 8. Evaluate the following 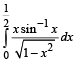 (1984 - 2 Marks)
(1984 - 2 Marks)
Ans. 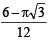
Solution.
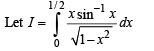
Put x = sinθ ⇒ dx =cosθ d θ
Also when x = 0, θ = 0
and when x = 1/2, θ = θ / 6
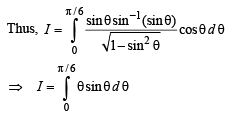
Intergrating the above by parts, we get
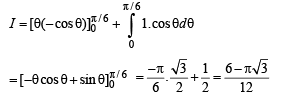
Q. 9. Find the area of the region bounded by the x-axis and the curves defined by (1984 - 4 Marks)
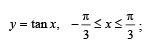
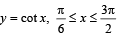
Ans. 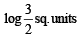
Solution. To find the area bold by x - axis and curves
y = tan x, -π/3 < x < π /3 … (1)
and y = cot x, π / 6 < x < 3π /2 … (2)
The curves intersect at P, where tan x = cot x, which is satisfied at x = π /4 within the given domain of x.
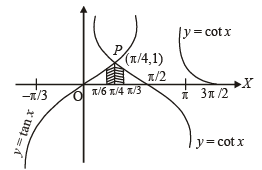
The required area is shaded area
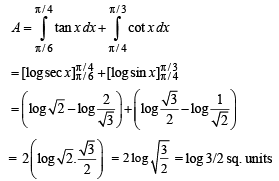
Q. 10. Given a function f(x) such that (1984 - 4 Marks)
(i) it is integrable over every interval on the real line and
(ii) f (t + x) = f (x), for every x and a real t, then show that the integral 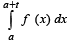 is independent of a.
is independent of a.
Solution.
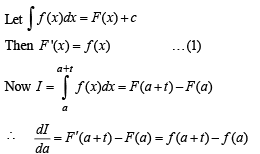

This shows that I is independent of a.
Q. 11. Evaluate the following 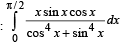 (1985 - 2½ Marks)
(1985 - 2½ Marks)
Ans. 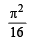
Solution.
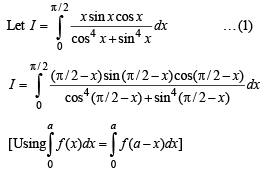
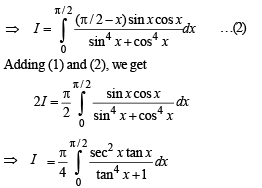
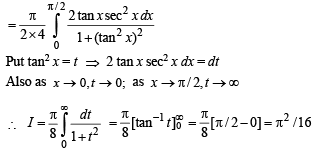
Q. 12. Sketch the region bounded by the curves 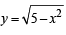 and y =| x - 1 | and find its area. (1985 - 5 Marks)
and y =| x - 1 | and find its area. (1985 - 5 Marks)
Ans. 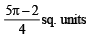
Solution. The given curves are

y =|x- 1| … (2)
We can clearly see that (on squaring both sides of (1)) eq. (1) represents a circle. But as y is + ve sq. root, ∴ (1) represents upper half of circle with centre (0, 0 ) and radius √5.
Eq. (2) represents the curve
Graph of these curves are as shown in figure with point of intersection of 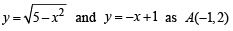 and of
and of 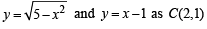
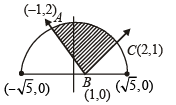
The required area = Shaded area
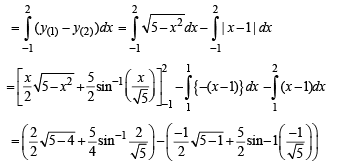
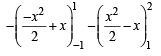
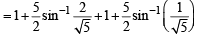
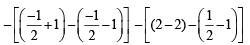
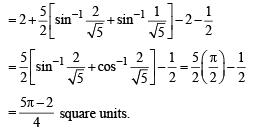
Q. 13. 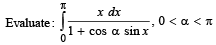 (1986 - 2½ Marks)
(1986 - 2½ Marks)
Ans. 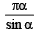
Solution.
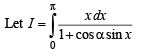 ...(1)
...(1)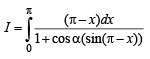
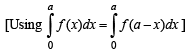
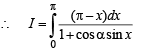 ...(2)
...(2)
Adding (1) and (2), we get
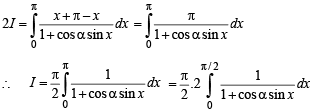
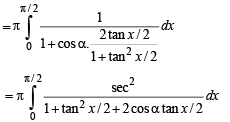
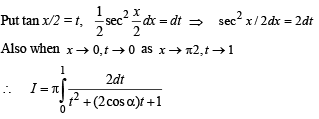
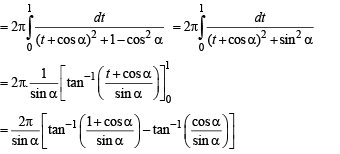
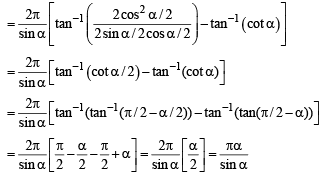
Q. 14. Find the area bounded by th e curves, x2 + y2 = 25, 4y = | 4 – x2 | and x = 0 above the x-axis. (1987 - 6 Marks)
Ans. 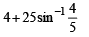
Solution. We have to find the area bounded by the curves
x2 +y2 = 25 ...(1)
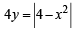 ...(2)
...(2)
x = 0 ...(3)
and above x-axis.
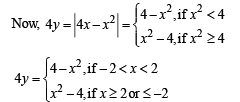
Thus we have three curves
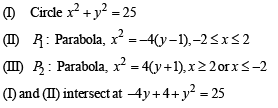
or (y - 2)2 = 52 ∴ y - 2 = ±5 y = 7,y =-3
y = – 3, 7 are rejected since.
y = – 3 is below x-axis and
y = 7 gives imaginary value of x. So, (I) and (II) do not intersect but II intersects x-axis at (2, 0) and (–2, 0). (I) and (III) intersect at
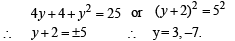
y = – 7 is rejected, y = 3 gives the points above x-axis. When y = 3, x = ±4. Hence the points of intersection of (I) and (III) are (4, 3) and (– 4, 3). Thus we have the shape of the curve as given in figure
. 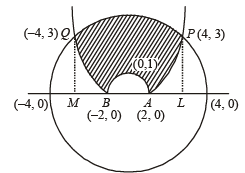
Required area is
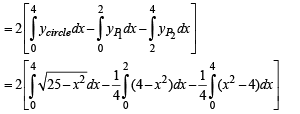
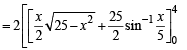
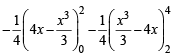
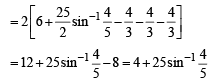
Q. 15. Find the area of the region bounded by the curve C : y = tan x, tangent drawn to C at x = π/4 and the x-axis. (1988 - 5 Marks)
Ans. 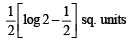
Solution. The given curve is y = tan x ...(1)
Let P be the point on (1) where x = π /4
∴ y = tan p / 4=1 i.e. co-ordinates of P are (π / 4,1)
∴ Equation of tangent at P is y - 1 = 2(x -π / 4)
or y = 2x + 1 -π/2 ...(2)
The graph of (1) and (2) are as shown in the figure.
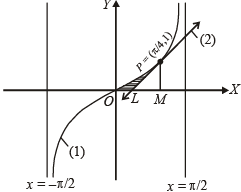
Tangent (2) meets x-axis at, 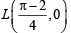
Now the required area = shaded area
= Area OPMO - Ar (ΔPLM)
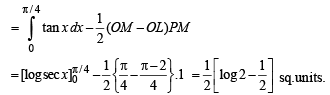
Q. 16. 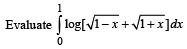 (1988 - 5 Marks)
(1988 - 5 Marks)
Ans. 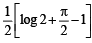
Solution.
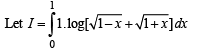
Intergrating by parts, we get
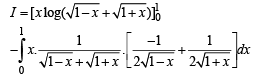
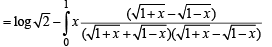
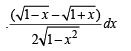
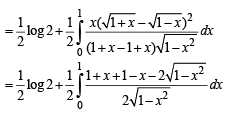
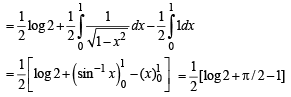
|
446 docs|929 tests
|
















