JEE Advanced (Subjective Type Questions): Matrices & Determinants | Chapter-wise Tests for JEE Main & Advanced PDF Download

Clear all your JEE doubts with EduRev Join for Free

Join for Free

Q.1. For what value of k do the following system of equations possess a non trivial (i.e., not all zero) solution over the set of rationals Q? 

x + ky + 3z = 0
 3x + ky – 2z = 0
 2x + 3y – 4z = 0 

For that value of k, find all the solutions for the system.                   (1979)

Ans.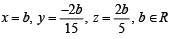 

Solution. We should have,

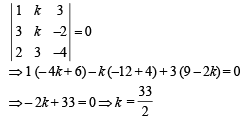
Substituting   and putting x = b, where b ∈ Q, we get the system as

33y + 6z = – 2b ...(1)
33y – 4z = – 6b ...(2)
3y – 4z = – 2b ...(3)

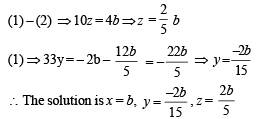
Q.2. Let a, b, c be positive and not all equal. Show that the value of the determinant    (1981 - 4 Marks)

Solution. The given det, on expanding along R₁, we get

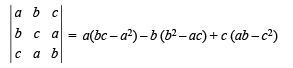
= 3abc – a³ – b³ – c³ = – (a³ + b³ + c³ – 3abc)
= – (a + b + c) [a² + b² + c² – ab – bc – ca]

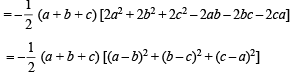
As a, b, c > 0
∴ a + b + c > 0
Also a ≠ b ≠ c
∴ (a – b)² + (b – c)²  + (c – a)² > 0
Hence the given determinant is – ve.

Q.3. Without expanding a determinant at any stage, show that

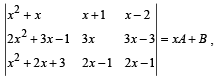 where A and B are determinants of order 3 not involving x. (1982 - 5 Marks)

Solution.

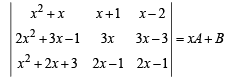
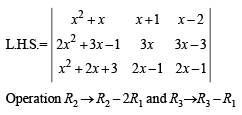
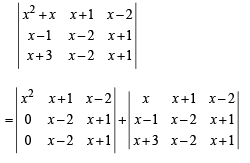
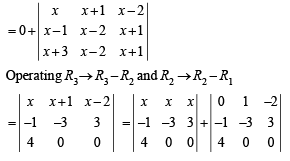
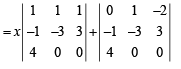
= xA + B = R.H. S
Hence Proved.

Q.4. Show that 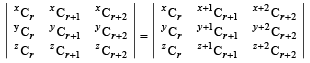  (1985 - 2 Marks)

Solution. On L.H.S.= D, applying operations C₂→ C₂ + C₁ and C₃→ C₃ + C₂ and using ⁿC_r + ⁿC_r+1 = ⁿ⁺¹C_r+1, we get

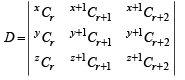
Operating C₃ + C₂ and using the same result, we get

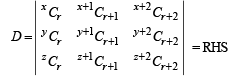
Hence proved

Q.5. Consider the system of linear equations in x, y, z : 

(sin 3θ) x – y + z = 0
 (cos 2θ) x + 4y + 3z = 0
 2x + 7y + 7z = 0 

Find the values of θ for which this system has nontrivial solutions.   (1986 - 5 Marks)

Ans. nπ or nπ + (-1)ⁿ π / 6, n ∈ Z

Solution. The system will have a non-trivial solution if

Expanding along C1, we get
⇒ (28 – 21) sin 3θ – (– 7 – 7) cos 2θ + 2 (– 3 – 4) = 0
⇒ 7 sin 3θ + 14 cos 2θ – 14 = 0
⇒ sin 3θ+ 2 cos 2θ – 2 = 0
⇒ 3 sin – 4 sin ³θ + 2 (1 – 2 sin²θ) – 2 = 0
⇒ 4 sin³θ + 4 sin ²θ – 3 sin θ = 0
⇒ sin θ (2 sinθ – 1) (2 sin θ + 3) = 0  
sin θ = 0 or sin θ = 1/2 (sin θ = – 3/2 not possible)
⇒ θ = nπ or θ = nπ + (–1)ⁿ π/6, n ∈ Z.

Q.6. 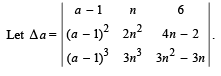Show that  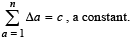     (1989 - 5 Marks)

Solution. We have

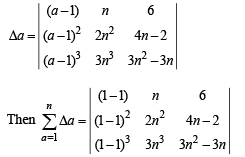
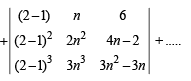
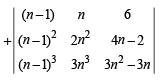
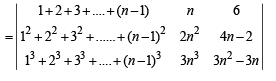
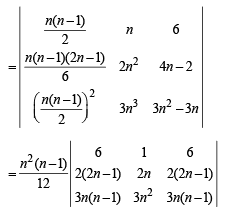
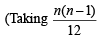 common from C₁ and n from C₂)

= 0 (as C₁ and C₃ are identical)

Thus,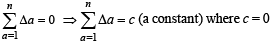 

Q.7. Let the three digit numbers A 28, 3B9, and 62 C, where A, B, and C are integers between 0 and 9, be divisible by a fixed integer k. Show that the determinant   is divisible by k.      (1990 -  4 Marks)

Solution. Given that A, B, C are integers between 0 and 9 and the three digit numbers A28, 3B9 and 62C are divisible by a fixed integer k.

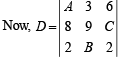
On operating R₂ → R₂ + 10 R₃ + 100 R₁, we get

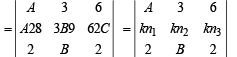
[As per question A28, 3B9 and 62C are divisible by k, therefore,

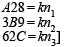
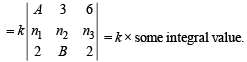
⇒ D is divisible by k.

Q.8. If a ≠ p, b ≠ q, c ≠ r and 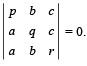 Then find the value of                     (1991 -  4 Marks)

Solution.

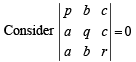
Operating R₁→ R₁– R₂ and R₂ → R₂ – R₃ we get

Taking (p – q), (q – b) and (r – c) common from C₁, C₂ and C₃ resp, we get

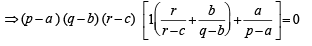
As given that  p ≠ a, q ≠ b, r ≠ c

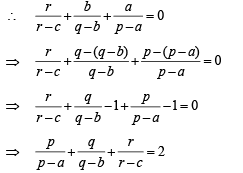
Q.9. For a fixed positive integer n, if 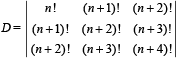  then show that  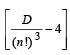is divisible by n.    (1992 -  4 Marks)

Solution.

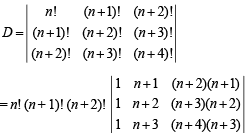
Operating R₂ → R₂ – R₁ and R₃ → R₃ – R₂, we get

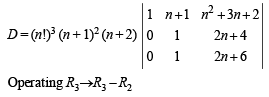
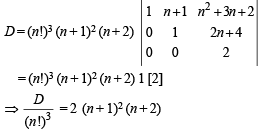
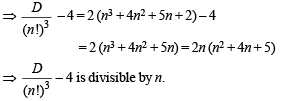
Q.10. Let λ and α be real. Find the set of all values of λ for which the system of linear equations                       (1993 -  5 Marks)

λx + (sin α) y+ (cos α) z = 0 , x + (cos α) y + (sin α) z = 0 , - x + (sin α) y - (cos α) z = 0 has a non-trivial solution. For λ = 1, find all values of α.

Solution. Given that λ, α ∈ R and system of linear equations
λx + (sin α) y + (cos α)z  = 0
x + (cos α) y + (sin α) z = 0
– x (sin α) y – (cos α) z = 0
has a non trivial solution, therefore D = 0

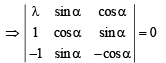
⇒ λ (– cos² α – sin²α) – sin α (– cos α + sin α)  + cos α(sin α + cos α) = 0
⇒ – λ + sin a cos α – sin² α + sin α cosα + cos²α = 0
⇒  λ = cos²α – sin²α + 2 sina cos α
⇒  λ = cos 2α + sin 2α

For l = 1, cos 2α + sin 2α = 1

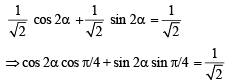
⇒ cos (2α – π/4) = cos p/4
⇒ 2α – π/4 = 2nπ ± π/4 ⇒ 2a = 2πr + π/4 + π/4; 2nπ – π/4 + π/4
⇒ α = nπ + p/4 or nπ

Q.11. For all values of A, B, C and P, Q, R show that     (1994 -  4 Marks)

Solution. L.H.S.

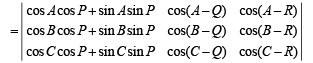
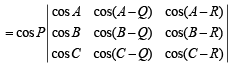
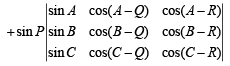
Operating; C₂→ C₂ – C₁ (cos Q); C₃→ C₃ – C₁ (cos R) on first determinant and C₂→ C₂ – (sin Q)C₁ and C₃→ C₃ – (sin R)C₁ on second determinant, we get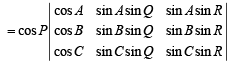

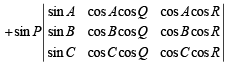
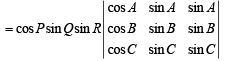
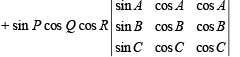
 = 0 + 0 [Both determinants become zero as C₂ ≡ C₃]
= 0 = R.H.S.

Q.12. Let a > 0,  d > 0. Find the value of the determinant         (1996 - 5 Marks)

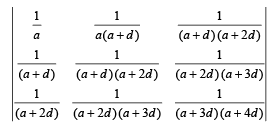
Ans.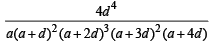 

Solution. Let us denote the given determinant by Δ Taking

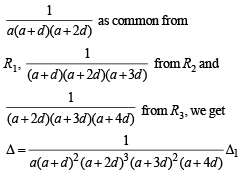
where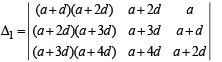

Applying R₃ → R₃ – R₂ and R₂ → R₂ – R₁, we get

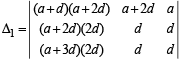
Applying R₃ → R₃ – R₂, we get

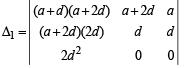
Expanding along R₃, we get

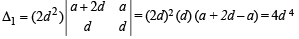
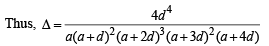
Q.13. Prove that for all values of θ,                            (2000 - 3 Marks)

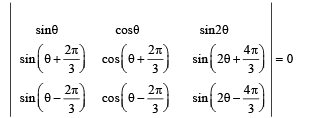
Solution. R₂ → R₂ + R₃,

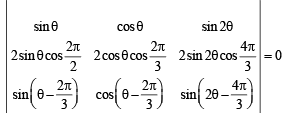
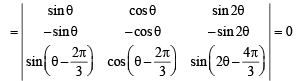
Q.14. If matrix 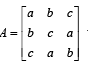  where a, b, c are real positivenumbers, abc = 1 and A^TA = I, then find the value of a³ + b³ + c³.             (2003 - 2 Marks)

Ans. 4

Solution. Given that ATA = I
⇒ |A^TA| = |A^T| |A| = |A| |A| = 1 [∵ | I | = I]
⇒ |A|² = 1           ....(1)

From given matrix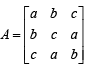  

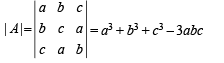   ....(2)

∴ (a³ + b³  + c³ – 3abc)² = 1 (From (1) and (2)]
⇒ a³ + b³ + c³ – 3abc = 1 or – 1
But for a³, b³, c³ using AM > GM

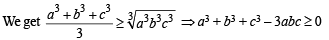
∴ We must have a³ + b³ + c³ – 3abc = 1
⇒ a³ + b³ + c³ = 1 + 3 × 1 = 4 [Using abc = 1]

Q.15. If M is a 3 × 3 matrix, where det M = 1 and MM^T = I, where ‘I’ is an identity matrix, prove that det (M – I) = 0.      (2004 - 2 Marks)

Solution. We are given that MM^T = I where M is a square matrix of order 3 and det. M = 1.
Consider det (M – I) = det (M – M M^T) [Given MM^T = I]
= det [M (I – M^T)]
= (det M) (det (I – M^T))     [∴|AB| = |A| |B|]
= – (det M) (det (M^T – I))
= – 1 [det (M^T – I)][Q det (M) =  1]
= – det (M – I)
[∴ det (M^T – I)  = det [(M – I)^T]  = det (M – I)]
⇒ 2 det (M – I) = 0 ⇒  det (M – I)  = 0
Hence Proved

Q.16. 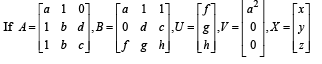 and AX = U has infinitely many solutions, prove that BX = V has no unique solution. Also show that if afd ≠ 0, then BX = V has no solution.      (2004 - 4 Marks)

Solution. Given that,

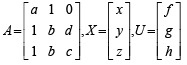
and AX = U has infinite many solutions.

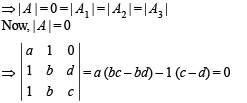
⇒ (ab – 1) (c – d) = 0
⇒  ab = 1 or c = d      ..........(1)

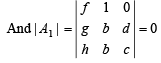
⇒ f (bc – bd) – 1 (gc – hd) = 0
⇒ f b (c – d) = gc – hd ...........(2)

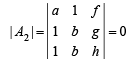
⇒ a (gc – hd) – f (c – d) = 0 ⇒ a (gc – hd) = f (c – d)

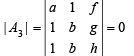
⇒ a(bh – bg) – 1(h – g) + f (b – b) = 0
⇒ ab (h – g) – (h – g) = 0
⇒ ab = 1 or h = g .........(3) Taking c = d
⇒ h = g and ab ≠ 1 (from (1), (2) and (3))
Now taking BX = V

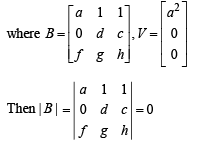
[∵In vew of c = d and g = h, C₂ and C₃ are identical]
⇒ BX = V  has no unique solution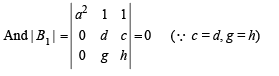

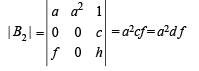     (∵ c = d)

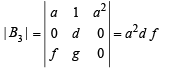
⇒ If adf ≠ 0 then | B₂ | = | B₃ | ≠ 0

Hence no solution exist.