JEE Advanced (Subjective Type Questions): Simple Harmonic Motion (Oscillations) | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. A mass M attached to a spring, oscillates with a period of 2sec. If the mass is increased by 2 kg the period increases by one sec. Find the initial mass M assuming that Hook’s Law is obeyed. (1979)
Ans. 1.6 kg
Solution. Key Concept:
The time period T of the spring is 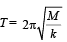

In the second case

From (i) and (ii)
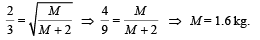
Q.2. Two masses m1 and m2 are suspended together by a massless spring of spring constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. Find the angular frequency and amplitude of oscillation of m2. (1981 - 3 marks)
Ans.
Solution.
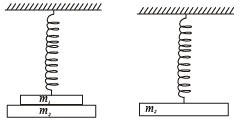
NOTE : When mass m1 is removed then the equilibrium will get disturbed. There will be a restoring force in the upward direction. The body will undergo S.H.M. now.
Let x1 be the extension of the spring when (m1 +m2) are suspended and x2 be the extension of spring when m1 is removed.
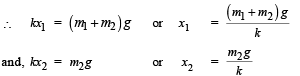
Amplitude of oscillation = x1-x2
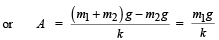
Let at any instant the mass m2 be having a displacement x from the mean position. Restoring force will be
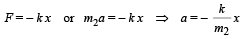
Comparing this with a = – ω2x,
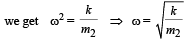
Q.3. Two light springs of force constants k1 and k2 and a block of mass m are in one line AB on a smooth horizontal table such that one end of each spring is fixed on rigid supports and the other end is free as shown in the figure. The distance CD between the free ends of the springs is 60 cms. If the block moves along AB with a velocity 120 cm/sec in between the springs, calculate the period of oscillation of the block (k1 = 1.8 N/m, k2 = 3.2 N/m, m = 200 gm) (1985 - 6 Marks)
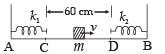
Ans. 2.83 sec.
Solution. The mass will strike the right spring, compress it. The K.E. of the mass will convert into P.E. of the spring. Again the spring will return to its natural size thereby converting its P.E. to K.E. of the block. The time taken for this process will
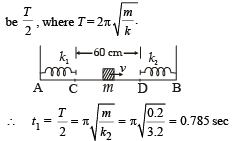
The block will move from A to B without any acceleration.
The time taken will be
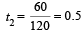
Now the block will compress the left spring and then the spring again attains its natural length. The time taken will be
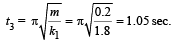
Again the block moves from B to A, completing one oscillation. The time taken for doing so
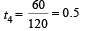
∴ The complete time of oscillation will be
= t1 + t2 + t3 + t4
= 0.785 + 0.5 + 1.05 + 0.5
= 2.83 (app.)
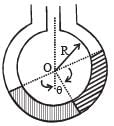
Q.4. Two non-viscous, incompressible and immiscible liquids of densities ρ and 1.5 ρ are poured into the two limbs of a circular tube of radius R and small cross section kept fixed in a vertical plane as shown in fig. Each liquid occupies one fourth the circumference of the tube. (1991 - 4 + 4 marks)
(a) Find the angle θ that the radius to the interface makes with the vertical in equilibrium position.
(b) If the whole is given a small displacement from its equilibrium position, show that the resulting oscillations are simple harmonic. Find the time period of these oscillations.
Ans.
Solution.
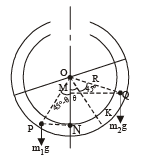
At equilibrium, taking torque of liquids about O
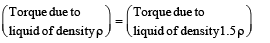
m2g × QM = m1g × PN
∴ m2g R sin (45° + θ) = m1gR sin (45° – θ)
VρgR sin (45° + θ) = 1.5VρgR sin (45° – θ)... (i)
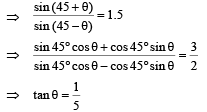
NOTE THIS STEP : Let us now displace the liquids in anticlockwise direction along the circumference of tube through an angle α.
The net torque
τ = m2gR sin (45° + θ + α) – m1gR sin (45° – θ – a)
= VρgR sin (45° + θ + α) – 1.5VρgR (45° – θ – a)
= VρgR sin (θ + 45°) cos α + VρgR cos (45° + θ)
sin α – 1.5 VρgR sin (45° – θ) cos α + 1.5 VρgR cos(45° – θ) sin α
Using eq. (i) we get
τ = VρgR [cos 45° + θ sin α + 1.5 cos 45° - θ) sin α ]
τ = VρgR [cos (45° + θ) + 1.5 cos (45° – θ)] sin α
when a is small (given)
∴ sin a ≈ α
t = VρgR [cos (45° + θ) + 1.5 cos (45° – θ)]α
Since, τ and α are proportional and directed towards mean position.
∴ The motion is simple harmonic.
Moment of inertia about O is
I = VρR2 + 1.5 VρR2

Q.5. Two identical balls A and B each of mass 0.1 kg, are attached to two identical massless springs. The spring-mass system is constrained to move inside a rigid smooth pipe bent in the form of a circle as shown in Fig. The pipe is fixed in a horizontal plane.
The centres of the balls can move in a circle of radius 0.06 π meter.
Each spring has a natural length zof 0.06 π meter and spring constant 0.1 N/m. Initially, both the balls are displaced by an angle θ = π / 6 radian with respect to the diameter PQ of the circle (as shown in Fig.) and released from rest. (1993 - 6 marks)
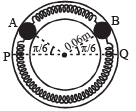
(i) Calculate the frequency of oscillation of ball B.
(ii) Find the speed of ball A when A and B are at the two ends of the diameter PQ.
(iii) What is the total energy of the system
Ans.
Solution. (i) As both the balls are displaced by an angle θ =π /6 radian with respect to the diameter PQ of the circle and released from rest. It results into compression of spring in upper segment and an equal elongation of spring in lower segment. Let it be x. PB and QA denote x in the figure.
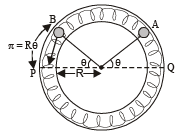
Compression = Rθ = elongation = x
∴ Force exerted by each spring on each ball = 2 kx
∴ Total force on each ball due to two springs = 4 kx
∴ Restoring torque about origin O =- (4kx)R
∴ τ = -4k (Rθ)R, where θ = Angular displacement
or τ = -4kR2θ
Since torque (τ) is proportional to θ, each ball executes angular SHM about the centre O.
Again, τ = -4kR2θ
or Iα = -4kR2θ where α = angular acceleration
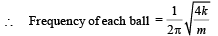
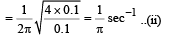
(ii) Let velocity at the mean position be vmax.
Loss in elastic potential energy = Gain in kinetic energy
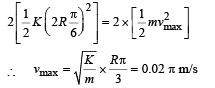
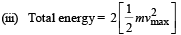
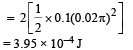
Q.6. A thin rod of length L and area of cross-section S is pivoted at its lowest point P inside a stationary, homogeneous and non-viscous liquid . The rod is free to rotate in a vertical plane about a horizontal axis passing through P. The density d1 of the material of the rod is smaller than the density d2 of the liquid.
The rod is displaced by a small angle θ from its equilibrium position and then released. Show that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters. (1996 - 5 Marks)
Ans.
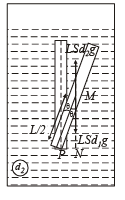
Solution. Let θ be the angle made by the rod at any instant t.
The volume of the rod = LS Weight of the rod = LS d1g
Upthrust acting on rod = LS d2g
Since, d2 > d1 (given). Therefore net force acting at the centre of mass of the rod at tilted position is (LS d2g – LSd1g)
Taking moment of force about P
τ = (LSd2g – LSd1g) × PN where PN = perpendicular distance of line of action of force from P

∵ Motion is simple harmonic.
On comparing it with τ = Cθ
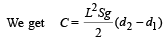
 ... (i)
... (i)
The moment of inertia I of the rod about P
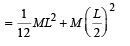
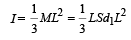 ... (ii)
... (ii)
From (i) and (ii)
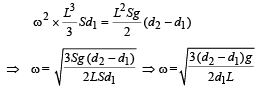
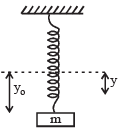
Q.7. A small body attached to one end of a vertically hanging spring is performing SHM about its mean position with angular frequency ω and amplitude a. If at a height y* from the mean position, the body gets detached from the spring, calculate the value of y* so that the height H attained by the mass is maximum. The body does not interact with the spring during its subsequent motion after detachment. (aω2 > g)
Ans.
Solution. If a small mass is attached to one end of a vertically hanging spring then it performs SHM.
Angular frequency = ω, Amplitude = a
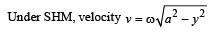
After detaching from spring, net downward acceleration of the block = g.
∴ Height attained by the block = h
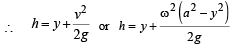
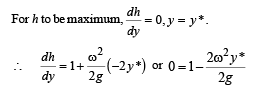

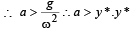 from mean position < a.
from mean position < a.
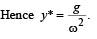
|
446 docs|929 tests
|
















