JEE Advanced (Subjective Type Questions): Thermodynamics- 1 | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. The enthalpy for the following reaction (ΔHº) at 25ºC are given below : (1981 - 2 Marks)
(i) 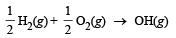 10.06 kcal
10.06 kcal
(ii)H2(g) → 2H(g) 104.18 kcal
(iii) O2(g) → 2O(g) 118.32 kcal
Calculate the O–H bond energy in the hydroxyl radical.
Ans. Sol. The required reaction in terms of dissociation energy is OH(g) → O(g) + H(g); ΔH = ?
This equation can be achieved by (a) reversing the equation (i), (b) dividing equation (ii) and (iii) each by 2, and (c) adding the three resulting equations.
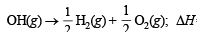 ΔH = + 10.06 kcal [Reversing eq (i)]
ΔH = + 10.06 kcal [Reversing eq (i)]
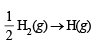
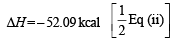
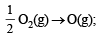
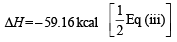
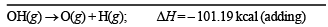
Thus one mole of OH(g) needs 101.19 kcal of energy to break into oxygen and hydrogen gaseous atoms. Hence the bond energy of O–H bond is 101.19 kcal.
Q.2. The molar heats of combustion of C2H2(g), C(graphite) and H2(g) are 310.62 kcal, 94.05 kcal and 68.32 kcal, respectively.
Calculate the standard heat of formation of C2H2(g). (1983 - 2 Marks)
Ans. Sol. The required equation is : 2C(s) + H2(g) → C2H2; ΔH = ?
Write the thermochemical equations for the given data
(i) 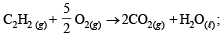
ΔH = –310.62 kcal
(ii)C(s) + O2(g) → CO2(g) ; ΔH = –94.05 kcal
(iii)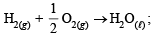 ΔH = –68.32 kcal
ΔH = –68.32 kcal
For getting the above required reaction, we will have to
NOTE :
(a) Bring C2H2 in the product that can be done by reversing the equation (i) to give equation (iv).
(b) Multiply equation (ii) by 2 to get 2C atoms in the reactants and thus equation (v) is obtained.
(c) Keep equation (iii) as such.
(d) Add equations (iv), (v) and (iii).
(iv) 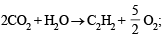 ΔH = 310.62 kcal
ΔH = 310.62 kcal
(v) 2C + 2O2 → 2CO2; ΔH = –188.10 kcal
(vi) 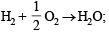 ΔH = –68.32 kcal
ΔH = –68.32 kcal
On adding, 2C + H2 → C2H2; ΔH = 54.20 kcal Hence the standard heat of formation of C2H2(g) = 54.20 kcal
Q.3. The heat energy, q, absorbed by a gas ΔH, is true at what condition(s). (1984 - 1 Mark)
Ans. Sol. If heat is absorbed at constant pressure, then qp = ΔE – (– PΔ V) or qp= E2 – E1 – [– P(V2 – V1)] or qp = (E2 + PV2) – (E1 + PV1) = H2 – H1 = ΔH
Q.4. Given the following standard heats of reactions : (i) heat of formation of water = –68.3 kcal; (ii) heat of combustion of acetylene = –310.6 kcal;
(iii) heat of combustion of eth ylene = –337.2 kcal; Calculate the heat of reaction for the hydrogenation of acetylene at constant volume (25ºC). (1984 - 4 Marks)
Ans. Sol. The given data can be written as follows
(i) 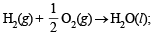 ΔH = –68.3 kcal
ΔH = –68.3 kcal
(ii) 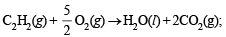
ΔH = –310.6 kcal
(iii) C2H4(g) + 3O2 → 2H2O(l) + 2CO2(g);ΔH = –337.2 kcal
The required thermochemical equation is C2H2(g) + H2(g) → C2H4(g) The required equation can be obtained by subtracting equation (iii) from the sum of equations (i) and (ii), thus ΔH of the required equation can be calculated as below.
ΔH = [–68.3 + (–310.6)] – (–337.2)
= [–68.3 – 310.6] + 337.2
= –378.9 + 337.2 = –41.7 kcal
ΔE, the heat of reaction for the hydrogenation of acetylene at constant volume is given by : ΔE = ΔH – ΔnRT
Here Δn = Moles of the gaseous products – Moles of the gaseous reactants
= 1 – (1 + 1) = –1
Substituting the values of ΔH, Δn, R and T in ΔE
= ΔH – ΔnRT
= –41.7 – (–1 × 2 × 10–3 × 298)
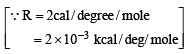
= –41.7 + 2 × 10–3 × 298
= –41.7 + 0.596 = 41.104 kcal
Q.5. The bond dissociation energies of gaseous H2, Cl2 and HCl are 104, 58 and 103 kcal/mole respectively. Calculate the enthalpy of formation of HCl gas. (1985 - 2 Marks)
Ans. Sol.
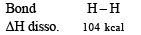
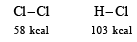
Formation of hydrogen chloride can be represented as H – H + Cl – Cl → 2H – Cl
Thus the reaction involves Cleavage of one H – H bond, ΔH = 104 kcal
Cleavage of one Cl – Cl bond, ΔH = 58 kcal
Formation of two H – Cl bonds, ΔH = 2 × – 103 kcal
∴ ΔH of the reaction = (104 + 58) – 2(103)
= 162 – 206 = – 44 kcal
Now since the enthalpy of formation of a compound is the change in heat content accompanied in the formation of one mole of the compound, the enthalpy of formation of
HCl gas = 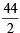 = – 22 kcal
= – 22 kcal
Q.6. The standard molar heats of formation of ethane, carbon dioxide and liquid water are –21.1, –94.1 and –68.3 kcal respectively. Calculate the standard molar heat of combustion of ethane. (1986 - 2 Marks)
Ans. Sol. The required chemical reaction. 2C2H6 + 7O2 —→ 4CO2 + 6H2O; ΔH = x
Note that since 2 moles of ethane are reacting, the ΔH of the reaction will be ½ x.
The thermochemical equations for the given data are written as below.
(i) C(s) + O2(g) —→ CO2(g); ΔH = –94.1 kcal
(ii)H2(g) + ½O2(g) —→ H2O(g); ΔH = –68.3 kcal
(iii) 2C(s) + 3H2(g) —→ C2H6(g); ΔH = –21.1 kcal
We know that ΔH = HProducts – HReactants
ΔH = 4ΔHCO2 + 6ΔHH2O – ( 2ΔHC2H6 + 7ΔHO2 )
ΔH = 4 × – 94.1 + 6 × – 68.3 – (2 × – 21.1 + 0)
= –376.4 – 409.8 + 42.2 = –744.0 kcal/2 mole of ethane
= –372.0 kcal/mole of ethane
Q.7. An intimate mixture of ferric oxide, Fe2O3, and aluminium, Al, is used in solid fuel rockets. Calculate the fuel value per gram and fuel value per cc of the mixture. Heats of formation and densities are as follows : (1988 - 2 Marks)
Hf (Al2O3) = 399 kcal/mole;
Hf (Fe2O3) = 199 kcal/mole;
Density of Fe2O3 = 5.2 g/cc;
Density of Al = 2.7 g/cc.
Ans. Sol. Fe2O3 + 2Al → 2Fe + Al2O3
2 × 56 + 48 = 160 2 × 27 = 54
Heat of reaction = 399 – 199 = 200 kcal
[Al & Fe are in their standard states]
Total weight of reactants = 160 + 54 = 214 g
∴ Fuel value/gram =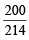 = 0.9346 kcal/g
= 0.9346 kcal/g
Volume of Al = 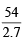 = 20 cc
= 20 cc
Volume of Fe2O3 =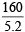 = 30.77 cc
= 30.77 cc
Total volume = 20 + 30.77 = 50.77 cc
∴ Fuel value per cc = 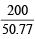 = 3.94 kcal/cc
= 3.94 kcal/cc
Q.8. An athlete is given 100 gm of glcuose (C6H12O6) of energy equivalent to 1560 kJ. He utilizes 50 percent of this gained energy in the event. In order to avoids storage of energy in the body, calculate the weight of water he would need to perspire. The enthalpy of evaporation of water is 44 kJ/ mole. (1989 - 2 Marks)
Ans. Sol. 100 g of glucose = 1560 kJ
Energy utilised in body = 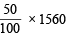 = 780 kJ
= 780 kJ
Energy left unutilised in body = 1560 – 780 = 780 kJ
Energy to be given out = 1560 – 780 = 780 kJ
Enthalpy of evaporation of water = 44 kJ/mole = 44 kJ/18 g of water [1 mole H2O = 18g water]
Hence amount water to be perspired to avoid storage of
energy = 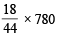 = 319.1 g
= 319.1 g
Q.9. The standard enthalpy of combustion at 25ºC of hydrogen, cyclohexene (C6H10) and cyclohexane (C6H12) are –241, –3800 and –3920 kJ/mole respectively. Calculate the heat of hydrogenation of cyclohexene. (1989 - 2 Marks)
Ans. Sol. The required reaction is
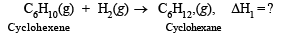 ...(1)
...(1)
The given facts can be written as :
H2(g)+ ½O2(g)→ H2O, ΔH2 = –241 kJ/mol ...(2)
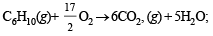 ΔH3 = –3800 kJ/mol ...(3)
ΔH3 = –3800 kJ/mol ...(3)
C6H12(g) + 9O2(g) → 6CO2(g) + 6H2O,
ΔH4 = –3920 kJ/mol ...(4)
The required reaction (1) can be obtained by adding equations (2) and (3) and subtracing (4) from the sum of (2) and (3).
C6H10(g)+ H2(g)→ C6H12(g) ΔH1 = (ΔH2 + ΔH3) – ΔH4
= [– 241 + (–3800)] – (– 3920)
= (– 241 – 3800) – (– 3920)
= – 4041 + 3920 = – 121 kJ/mole
Q.10. Using the data (all values are in kcal mol–1 at 25ºC) given below, calculate the bond energy of C–C and C–H bonds. (1990 - 5 Marks)
ΔHºcombustion(ethane) = –372.0
ΔHºcombustion(propane) = –530.0
ΔHºC(s) → C(g) = 172.0
Bond energy of H–H = 104.0
ΔHºf of H2O(l) = –68.0
ΔHºf of CO2(g) = –94.0
Ans. Sol. For C3H8 : 3C + 4H2 → C3H8; ΔH1 = ?
For C2H6 : 2C + 3H2 → C2H6; ΔH2 = ?
∴ ΔH1 = –[2(C–C) + 8(C–H)] + [3Cs→g + 4(H–H)] ...(1)
∴ ΔH2 = –[1(C–C) + 6(C–H)] + [2Cs→g + 3(H–H)] ...(2)
Let bond energy of C–C be x kcal and bond energy of C–H be y kcal
∴ By eq. (1) ΔH1 = –(2x + 8y) + [3 × 172 + 4 × 104] ...(3)
ΔH2 = –(x + 6y) + [2 × 172 + 3 × 104] ...(4)
Also given C + O2 → CO2; ΔH = –94.0 k cal ...(5)
H2 + ½O2 → H2O; ΔH = –68.0 kcal ...(6)
C2H6 + (7/2)O2 → 2CO2 + 3H2O; ΔH = –372 k cal ...(7)
C3H8 + 5O2→ 3CO2 + 4H2O; ΔH = –530 k cal ...(8)
By inspection method : 2 × (5) + 3 × (6) – (7) gives 2C + 3H2 → C2H6; ΔH2 = –20 k cal ...(9)
and 3 × (5) + 4 × (6) – (8) gives 3C + 4H2 → C3H8; ΔH1 = –20 k cal ...(10)
∴ By eq. (3), (4), (9) and (10) x + 6y = 6762x + 8y = 956
∴ x = 82 k cal and y = 99 k cal Bond energy of C–C bond = 82 k cal and Bond energy of C–H bond = 99 k cal
Q.11. A gas mixture of 3.67 litres of ethylene and methane on complete combustion at 25ºC produces 6.11 litres of CO2.
Find out the amount of heat evolved on burning one litre of the gas mixture. The heats of combustion of ethylene and methane are –1423 and –891 kJ mol–1 at 25ºC. (1991 - 5 Marks)
Ans. Sol. Combustion of C2H4 and CH4 takes place as follows :
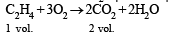
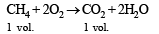
Let the vol. of CH4 in mixture = xl
∴ Vol. of C2H4 in the mixture = (3.67 – x)l
Vol. of CO2 produced by x l of CH4 = x l and
Vol. of CO2 produced by (3.67 – x) l of C2H4 = 2 (3.67 – x) l
∴ Total vol. of CO2 produced = x + 2 (3.67 – x)
or 6.11 = x + 2 (3.67 – x) or x = 1.23 l
∴ Vol. of CH4 in the mixture = 1.23 l
and Vol. of C2H4 in the mixture = 3.67 – 1.23 = 2.44 l
Vol. of CH4 per litre of the mixture 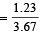 = 0.335 l
= 0.335 l
Vol. of C2H4 per litre of the mixture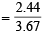 = 0.665 l
= 0.665 l
Now we know that volume of 1 mol. of any gas at
25ºC (298 K) =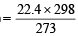 = 24.45 l
= 24.45 l
[∵ Volume at NTP = 22.4L]
Heat evolved due to combustion of 0.335 l of CH4
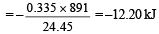 [given, heat evolved by
[given, heat evolved by
combustion of 1l = 891 kJ]
Similarly, heat evolved due to combustion of 0.665 l of C2H4
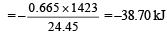
∴ Total heat evolved = 12.20 + 38.70 = 50.90 kJ
Q.12. Determine the enthalpy change of the reaction.
C3H8(g) + H2(g) → C2H6(g) + CH4(g), at 25º, using the given heat of combustion values under standard conditions:
Compound H2(g) CH4(g) C2H6(g) C(graphite)
ΔHº (kJ/mol) – 285.8 –890.0 –1560.0 –393.5
The standard heat of formation of C3H8(g) is –103.8 kJ/mol. (1992 - 3 Marks)
Ans. Sol. From the given data, we can write :
(i)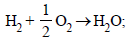 ΔH1 = –285.8 kJ/mol
ΔH1 = –285.8 kJ/mol
(ii)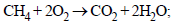 ΔH2 = –890 kJ mol
ΔH2 = –890 kJ mol
(iii)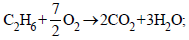 ΔH3 = –1560 kJ/mol
ΔH3 = –1560 kJ/mol
(iv) C(s) + O2 → CO2; ΔH4 = –393.5 kJ/mol
(v) 3C(s) + 4H2 → C3H8(g); ΔH5 = –103.8 kJ/mol
The required reaction is C3H8(g) + H2(g) →C2H6(g) +
CH4(g), ΔH = ?
It can be obtained by the following calculations.
3 × (iv)–(v) + 5(i) – (iii) – (ii)
In other words, ΔH = 3ΔH4 – ΔH5 + 5ΔH1 – ΔH2 – ΔH3
∴ΔH = 3(–393.5) – (–103.8) + 5(–285.8) + 890 + 1560
= –2609.5 + 2553.8 = –55.7 kJ/mol
Q.13. In order to get maximum calorific output, a burner should have an optimum fuel to oxygen ratio which corresponds to 3 times as much oxygen as is required theoretically for complete combustion of the fuel. A burner which has been adjusted for methane as fuel (with x litre/hour of CH4 and 6x litre/hour of O2) is to be readjusted for butane, C4H10. In order to get the same calorific output, what should be the rate of supply of butane and oxygen ? Assume that losses due to incomplete combustion, etc, are the same for both the fuels and the gases behave ideally. (1993 - 3 Marks)
Heats of combustion : CH4 = 809 kJ / mol; C4 H10= 2878 kJ / mol
Ans. Sol. Combustion of CH4 and C4H10 takes place as follows
CH4 + 2O2 → CO2 + 2H2O, ΔH = –809 kJ mol–1
C4H10 + 13/2O2 → 4CO2 + 5H2O, ΔH = –2878 kJ mol–1
In order to get the same calorific output due to C4H10,
the rate of supply of butane 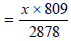 = 0.281 x l/hr
= 0.281 x l/hr
= 5.481 x l/hr
Rate of supply of oxygen = 0.2803 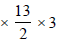 = 5.481 x l/hr
= 5.481 x l/hr
Q.14. The polymerisation of ethylene to linear polyethylene is represented by the reaction (1994 - 2 Marks)
nCH2 = CH2—→ —[ CH2- CH2 —]n where n has a large integral value. Given that the average enthalpies of bond dissociation for C = C and C– C at 298 K are + 590 and + 331 kJ mol–1, respectively, calculate the enthalpy of polymerisation per mole of ethylene at 298 K.
Ans. Sol. nCH2 = CH2 → (CH2 – CH2)n
NOTE : During the polymerisation of ethylene, one mole of
ethylene breaks i.e. one C = C double bond breaks and the
two CH2 – groups are linked with C – C single bonds thus
forming three single bonds (two single bonds are formed
when each CH2 – group of ethylene links with one CH2 –
group of another ethylene molecule). But in the whole unit of polymer, number of single C–Cbonds formed/mole of
ethylene is 2.
Energy released = Energy due to formation of 2 C–C single
bonds
= 2 × 331 = 662 kJ/mol of ethylene
Energy absorbed = Energy due to dissociation of 1 C=C
double bond
= 590 kJ/mol of ethylene
∴Enthalpy of polymerisation/mol of ethylene or
ΔHpolymerisation = 590 – 662 kJ/mol = –72 kJ/mole
Q.15 A fixed mass 'm' of a gas is subjected to transformation of states from K to L to M to N and back to K as shown in the figure
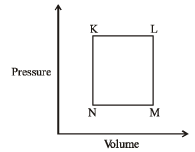
Q. The succeeding operations that enable this transformation of states are
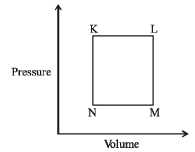
K → L ⇒ V increasing at constant P Hence T increases (Heating)
L → M ⇒ P decreasing at constant V Hence T decreases (Cooling)
M → N ⇒ V decreasing at constant P Hence T decreases (Cooling)
N → K ⇒ P increasing at constant V Hence T increases (Heating)
Q.16 A fixed mass 'm' of a gas is subjected to transformation of states from K to L to M to N and back to K as shown in the figure
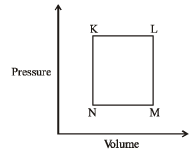
Q. The pair of isochoric processes among the transformation of states is
|
446 docs|929 tests
|





















