JEE Advanced (Subjective Type Questions):Thermodynamics- 2 | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.15. The standard molar enthalpies of formation of cyclohexane(l)and benzene(l) at 25°C are – 156 and + 49 kJ mol^–1 respectively. The standard enthalpy of hydrogenation of cyclohexene(l) at 25° C is –119 kJ mol^–1. Use these data to estimate the magnitude of the resonance energy of benzene. (1996 - 2 Marks) 

Ans. Sol. Standard enthalpy of hydrogenation of cyclohexene (–119kJ mol^–1) means the enthalpy of hydrogenation of one C = C double bond. Now benzene has three C = C double bonds, the enthalpy of the reaction would be = 3 × – 119 = – 357 kJ mol^–1

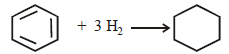
Actual enthalpy of the reaction can be evaluated as follows.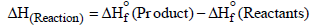

–156– (49 0) – 205 kJ mol
∴Resonance energy = ΔH_Exp – ΔH_cal
= –357 – (–205) = –152kJ mol^–1

Q.16. Compute the heat of formation of liquid methyl alcohol in kilojoules per mole, using the following data. Heat of vaporization of liquid methyl alcohol = 38 kJ/mol. Heat of formation of gaseous atoms from the elements in their standard states; H, 218 kJ/mol; C, 715 kJ/mol; O, 249kJ / mol.
 Average bond energies : C – H = 415kJ/mol, C – O = 365 kJ/mol, O – H = 463 kJ/mol (1997 - 5 Marks) 

Ans. Sol. The required thermochemical equation is

C(g) + 4H(g) + O(g)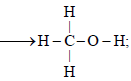 Δ H_f  = ?

Δ H_f  =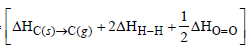

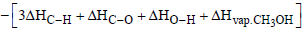
    = [715 + 2 × 436 +249] – [3 ×  415 +  356 + 463 + 38 ]
          = – 266 kJ mol^–1

Q.17. Anhydrous AlCl₃ is covalent. From the data given below, predict whether it would remain covalent or become ionic in aqueous  solution. (Ionisation energy for Al = 5137 kJ mol^–1; ΔH_hydration for Al3+ = –4665 kJ mol^–1; ΔH_hydration for Cl– = – 381 kJ mol^–1.) (1997 - 2 Marks) 

Ans. Sol. TIPS/Formulae : For ionisation ΔH_ionisation > ΔH_Hydration
Total hydration energy of Al³⁺ & 3Cl– ions of AlCl₃ ( ΔH_hydration) = (Hydration energyof Al³⁺ + 3 x Hydration energy of Cl–) = [–4665 + 3 (–381)]kJ mole^–1  = –5808 kJ mole^–1 NOTE : This amount of energy is more than that required for the ionisation of Al into Al³⁺ (Ionisation energy of Al to Al³⁺= 5137 kJ mol^–1).
Due to this reason, AlCl₃ becomes ionic in aqueous solution. In aqueous solution it exists in ionic form as below AlCl₃ + 6H₂O → [Al(H₂O)₆]³⁺ + 3Cl– AlCl₃ + aq. → AlCl₃(aq.); ΔH = ?
ΔH = Energy released during hydration – Energy used during ionisation        
= –4665 – 3 x 381 + 5137 = – 671 kJ/mol
Thus formation of ions will take place.

Q.18. From the following data, calculate the enthalpy change for the combustion of cyclopropane at 298 K. The enthalpy of formation of CO₂(g), H₂O(l) and propene(g) are – 393.5, – 285.8 and 20.42 kJ mol^–1 respectively. The enthalpy of isomerisation of cyclopropane to propene is – 33.0 kJ mol^–1. (1998 -  5 Marks)

Ans. Sol. 

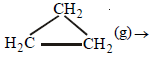(g) → CH₃CH = CH₂(g); ΔH = –33.0 kJ ...(i)
C + O₂ → CO₂(g); ΔH = – 393.5kJ ...(ii)
H₂ + 1/2O₂ → H₂O(l); ΔH = – 285.8 kJ ...(iii)
3C + 3H₂ → CH₃–CH = CH₂(g);  ΔH = 20.42 kJ ...(iv)

The required reaction is

 
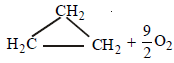
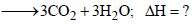
To calculate the value of ΔH follow the following steps. (iv) – (i) yields

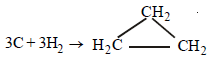; ΔH = 53.42 kJ ...(v)

[3 x (ii) + 3 x (iii)] – (v) yields ]

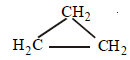+ (9/2)O₂ → 3CO₂ + 3H₂O;

ΔH = –2091.32 kJ

Q.19. Estimate the average S–F bond energy in SF₆. The values of standard enthalpy of formation of SF₆(g), S(g)and F(g) are : – 1100, 275 and 80 kJ mol^–1 respectively. (1999 - 3 Marks) 

Ans. Sol. Given  S(s) + 3F₂(g) → SF₆(g) ; ΔH = –1100 kJ .....(i)
S(S) → S(g); ΔH = 275 kJ .....(ii)
1/2 F₂(g) → F(g); ΔH = 80 kJ .....(iii)
To get SF₆(g) →  S(g) + 6F(g) we can proceed as (ii) + 6 x (iii) - (i)
∴ SF₆(g) → S(g) + 6F(g); ΔH= 1855 kJ
Thus average bond energy for S-F bond = 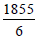= 309.16kJ

Q.20. A sample of argon gas at 1 atm pressure and 27°C expands reversibly and adiabatically from 1.25 dm³ to 2.50 dm³.
 Calculate the enthalpy change in this process. CV, m for argon is 12.48 JK^–1 mol^–1. (2000 - 4 Marks)

Ans. Sol. TIPS/Formulae : For adiabatic expansion, we have

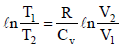 and 

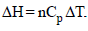
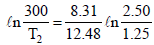Solving, we get, T₂ = 188.5 K

No. of moles of argon gas, n  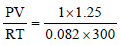= = 0.05

Now we know that ΔH = nC_pΔT = 0.05 x 20.8(188.5 - 300) =-115.41 Joules
[∵C_p=C_v+R=12.48 + 8.314 = 20.8]

Q.21. Show that the reaction 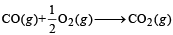    at 300 K, is spontaneous and exothermic, when the standard entropy change is –0.094 kJ mol^–1 K^–1. The standard Gibbs free energies of formation for CO₂ and CO are –394.4 and –137.2 kJ mol^–1, respectively. (2000 - 3 Marks) 

Ans. Sol. For following reaction

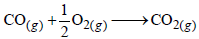
ΔG° can be calculated as follows :

ΔG° = DG_p° - ΔG°_R =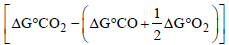 

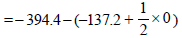= – 257.2 kJ mol^–1

Since, ΔG° = ΔH°-TΔS₀    or – 257.2 = ΔH– 300(0.094)
∴ΔH°= – 285.4 kJ/mol Since,
NOTE : ∴ΔH° is negative, so the reaction is exothermic and since ΔG° is negative so the reaction is spontaneous.

Q.22. Diborane is a potential rocket fuel which under goes combustion according to the reaction. (2000 - 2 Marks) B₂H₆(g) + 3O₂(g) → B₂O₃(s) + 3H₂O (g) From the following data, calculate the enthalpy change for the combustion of diborane.

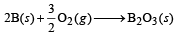ΔH = –1273 kJ mol^–1

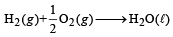 ΔH = – 286 kJ mol^–1

H₂O (l) —→ H₂O(g) ΔH = 44 kJ mol^–1 

2B(s) + 3H₂(g) —→ B₂H₆(g) ΔH = 36 kJ mol^–1

Ans. Sol. The chemical reaction for combustion of diborane is B₂H₆ (g) + 3O₂(g)  —→ B₂O₃ (s) + 3H₂O (g), ΔH = ?
For this the enthalpy change can be calculated in the following way.
ΔH = [ΔHB₂O₃ (s) + 3ΔHH₂O(g) ] -ΔHB₂H₆ (g) ; (∵ ΔH_f° of O₂ = 0)
ΔHH₂O(g) can be obtained by adding ΔHH₂O(l) and ΔH H₂O(g) , i.e. – 286 + 44 = – 242 kJ mol^–1
ΔH = [–1273 + 3 × – 242] – 36 kJ mol^–1 = – 1273 – 726 – 36      
 = –2035 kJ mol^–1

Q.23. When 1-pentyne (A) is treated with 4 N alcoholic KOH at 175°C, it is converted slowly into an equilibrium mixture of 1.3% 1-pentyne (A), 95.2% 2-pentyne (B) and 3.5% of 1, 2-pentadiene (C). The equilibrium was maintained at 175°C.
 Calculate ΔG° for the following equilibria :

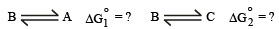
From the calculated value of ΔG₁^° and ΔG^°₂ indicate the order of stability of (A), (B) and (C). Write a reasonable reaction mechanism showing all intermediates leading to (A), (B) and (C). (2001 - 10 Marks)

Ans. Sol. TIPS/Formulae :

Calculation of ΔG values :

Thus for the equilibrium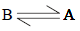 

ΔG₁° = (-2.303 x 8.314 x 448)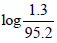 

or  ΔG₁° = 15.992 kJ mole ^-1

Similarly for the equilibrium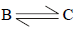  

ΔG°₂ = (-2.303 x 8.314 x 448)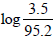

or  ΔG°₂ = 12.312kJ mole^-1

Similarly for equilibrium,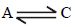

ΔG° = -8.314 x 448 x 2.303 x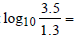= - 3.688 kJ mole^-1

Hence, we have that

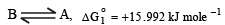
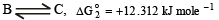
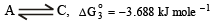
Thus, the correct order of stability, B > C > A

NOTE : Mechanism of isomerisation

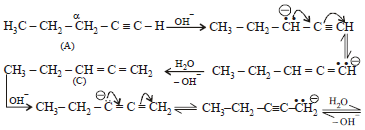
Q.24. Two moles of a per fect gas undergo th e followin g pr ocess es: (2002 - 5 Marks) (a) a reversible isobaric expansion from (1.0 atm, 20.0L) to (1.0 atm, 40.0 L); (b) a r eversible isochoric chan ge of state fr om (1.0 atm, 40.0 L) to (0.5 atm, 40.0 L); (c) a reversible isothermal compression from (0.5 atm, 40.0 L) to (1.0 atm, 20.0 L). (i) Sketch with labels each of the processes on the same P-V diagram. (ii) Calculate the total work (w) and th e total h eat change (q) involved in the above processes. (iii) What will be the values of ΔU, ΔH and ΔS for the overall process?

Ans. Sol. 

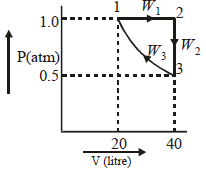
(ii) Total work (W) = W₁ + W₂ + W₃

= - PΔV + 0+ 2.303RT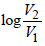 

= -1 x 20 + 2.303 x 2 x 0.082 x121.95 log2      
 = – 20 + 13.87 = – 6.13 L atm

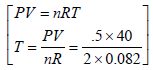=  121.95 K

Since the system has returned to its initial state i.e. the process is cyclic, so ΔU= 0,
ΔU = q +W= 0,  so q = –W = – (– 6.13) L.atm = 620.7 J
 NOTE :  In a cyclic process heat absorbed is completely converted into work. (iii) Entropy is a state function and since the system has returned to its initial state, so ΔS = 0 . Similarly ΔH = 0 and ΔU = 0 for the same reason i.e. U and H are also state functions having definite values in a given state of a system.

Q. 25. C_v value of He is always 3R/2 but C_v value of H₂ is 3R/2 at low temperature and 5R/2 at moderate temperature and more than 5R/2 at higher temperature explain in two to three lines. (2003 - 2 Marks)

Ans. Sol. Helium molecule is monoatomic so it has just three degrees of freedom corresponding to the three translational motion at all temperature and hence Cv value is always 3/2 R.
Hydrogen molecule is diatomic which are not rigidly held so they vibrate about a well defined average separation. For hydrogen molecule we have rotational and vibrational motion both besides translational motion. These two additional contributions  increase its total heat capacity.
Contribution from vibrational motion is not appreciable at low temperature but increases from 0 to R on raising temperature.

Q. 26. An insulated container contains 1 mol of a liquid, molar volume 100 ml, at 1 bar. When liquid is steeply pressed to 100 bar, volume decreases to 99 ml. Find. ΔH and ΔU for the pr ocess. (2004 - 2 Marks)

Ans. Sol. TIPS/Formulae : For adiabatic process, W = P (V₂ – V₁)
Here P₁ = 1 bar, P₂ = 100 bar, V₁ = 100 mL, V₂ = 99 mL;
For adiabatic process, q = 0  ∴ ΔU = w  
ΔU = q + W  = q – P(V₂ – V₁)
since W = – P(V₂ – V₁)= 0 – 100 (99 – 100) = 100 bar mL  
ΔH = ΔU + Δ(PV) = ΔU + (P₂V₂ – P₁V₁)
= 100 + [(100 × 99) – (1 × 100)]
= 100 + ( 9900 – 100) = 9900 bar mL

Q. 27. In the following equilibrium N₂O₄(g) 2NO₂(g) (2004 - 2 Marks) When 5 moles of each is taken and the temperature is kept at 298 K, the total pressure was found to be 20 bar.
 Given : ΔG_fº (N₂O₄) = 100kJ; ΔG_fº (NO₂) = 50 kJ (i) Find ΔG of the reaction at 298 K. (ii) Find the direction of the reaction 

Ans. Sol. (i)  

Initially p N2O4 = p NO2= 10

Reaction quotient =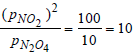 

ΔG° = 2 ΔG°_f ( NO₂) - ΔG°_f ( N₂O₄) = 100- 100= 0
ΔG  =  ΔGº – 2.303 RT log K_p          
= 0 – 2.303 × 298 log10 = – 56.0304 L atm.

(ii) The negative value of ΔG indicates that the reaction is spontaneous & will lie in the right direction, (forward).

Q.28. For the reaction, 2CO + O₂—→ 2CO₂ ; ΔH = -560kJ. Two moles of CO and one mole of O₂ are taken in a container of volume 1 L. They completely form two moles of CO₂, the gases deviate appreciably from ideal behaviour. If the pressure in the vessel changes from 70 to 40 atm, find the magnitude (absolute value) of ΔU at 500 K. (1 L atm = 0.1 kJ) (2006 - 6M)

Ans. Sol. ΔH = ΔU+ Δ(PV ) = ΔU + V ΔP (∵ ΔV= 0)
or ΔU = ΔH - V ΔP = -560- [1(40 - 70)x 0.1]
=-560 + 3 =-557 kJ mol^–1
So the magnitude is 557 kJ mol^–1.
∵ ΔG° = – 2.303RT log K_p at equilibrium ΔG° = 0
∴ – 2.303RT log K_p = 0 ⇒ log K_p = 0 or K_p = 1