JEE Exam > JEE Notes > Mathematics (Maths) for JEE Main & Advanced > JEE Advanced Previous Year Questions (2018 - 2024): Mathematical Induction and Binomial Theorem
JEE Advanced Previous Year Questions (2018 - 2024): Mathematical Induction and Binomial Theorem | Mathematics (Maths) for JEE Main & Advanced PDF Download
2023
Q1: Let a and b be two nonzero real numbers. If the coefficient of x5 in the expansion of  is equal to the coefficient of x−5 in the expansion of
is equal to the coefficient of x−5 in the expansion of 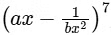 , then the value of 2b is : [JEE Advanced 2023 Paper 1]
, then the value of 2b is : [JEE Advanced 2023 Paper 1]
Ans: 3
here 8 - 3r = 5
8 - 5 = 3r
∴ r = 1
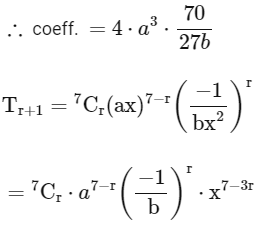
7 - 3r = 5
⇒ 12 = 3r
∴ r = 4
now, 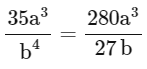
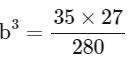
⇒ b = 3/2
∴ 2b = 3
2020
Q1: For non-negative integers s and r, let
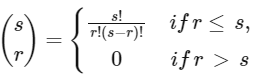
For positive integers m and n, let
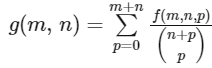
where for any non-negative integer p,
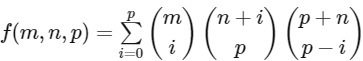
Then which of the following statements is/are TRUE?
(a) g(m, n) = g(n, m) for all positive integers m, n
(b) g(m, n + 1) = g(m + 1, n) for all positive integers m, n
(c) g(2m, 2n) = 2g(m, n) for all positive integers m, n
(d) g(2m, 2n) = (g(m, n))2 for all positive integers m, n [JEE Advanced 2020 Paper 2]
Ans: (a), (b) & (d)
Since,
(a) g(m, n) = g(n, m) for all positive integers m, n
(b) g(m, n + 1) = g(m + 1, n) for all positive integers m, n
(c) g(2m, 2n) = 2g(m, n) for all positive integers m, n
(d) g(2m, 2n) = (g(m, n))2 for all positive integers m, n [JEE Advanced 2020 Paper 2]
Ans: (a), (b) & (d)
Since,
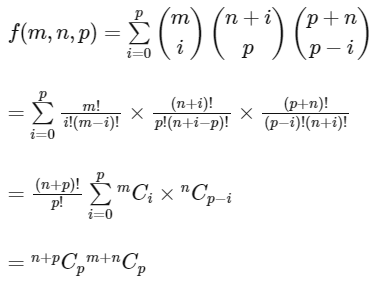
Since, 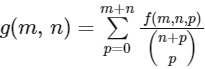
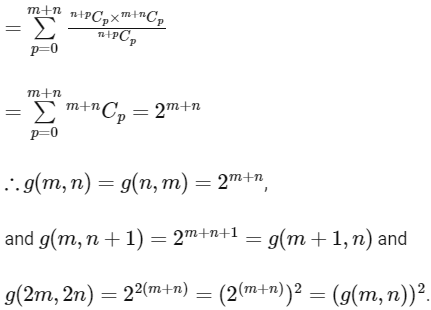
2018
Q1: Let 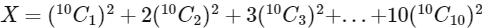 where
where 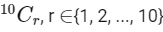 denote binomial coefficients. Then, the value of
denote binomial coefficients. Then, the value of 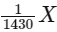 is _____. [JEE Advanced 2018 Paper 2]
is _____. [JEE Advanced 2018 Paper 2]
Ans: 646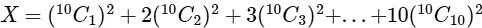
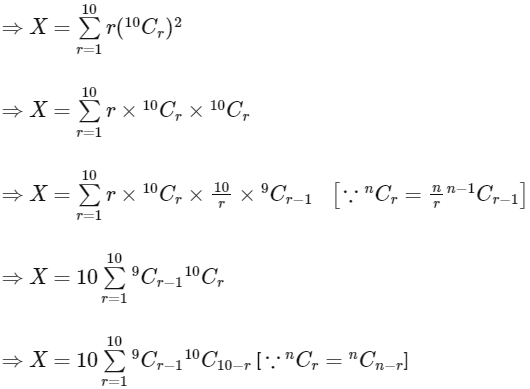
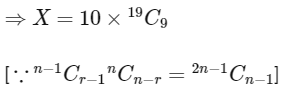
Now, 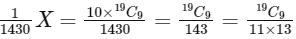
= 19 x 17 x 16 / 8
= 19 x 34
= 646
The document JEE Advanced Previous Year Questions (2018 - 2024): Mathematical Induction and Binomial Theorem | Mathematics (Maths) for JEE Main & Advanced is a part of the JEE Course Mathematics (Maths) for JEE Main & Advanced.
All you need of JEE at this link: JEE
|
172 videos|503 docs|154 tests
|
Related Searches
















