JEE Advanced Previous Year Questions (2018 - 2024): Units & Measurements | Physics for JEE Main & Advanced PDF Download
2024
Q1: The dimensions of a cone are measured using a scale with a least count of 2mm. The diameter of the base and the height are both measured to be 20.0cm. The maximum percentage error in the determination of the volume is _______. [JEE Advanced 2024 Paper 2]
Ans: 3
To determine the maximum percentage error in the volume of the cone, we first need to understand the dependence of the cone's volume on its dimensions: the diameter of the base and its height.
The volume V of a cone is given by the formula:
V = 13 πr²h
where r is the radius of the base and h is the height.
Given that both the diameter (D) of the base and the height (h) are measured to be 20.0 cm, we can find the radius r as follows:
r = D2 = 20.0 cm2 = 10.0 cm
Now, let's denote the errors in measuring the diameter and height as ΔD and Δh respectively.
Since the measurements are taken with a scale having a least count of 2 mm, we have:
ΔD = 2 mm = 0.2 cm
Δh = 2 mm = 0.2 cm
To find the maximum percentage error in the volume, we need to use the formula for the propagation of relative errors.
Considering the volume formula V = 13 πr²h, the relative errors in r and h will propagate into the volume as follows:
The relative error in the radius Δr/r is:
Δrr = ΔDD = 0.2 cm20.0 cm = 0.01
The relative error in the height Δh/h is:
Δhh = 0.2 cm20.0 cm = 0.01
Since V is proportional to r² and h, the total relative error in the volume is given by:
ΔVV = 2 Δrr + Δhh
Substituting the relative errors, we get:
ΔVV = 2(0.01) + 0.01 = 0.02 + 0.01 = 0.03
Hence, the maximum percentage error in the volume is:
0.03 × 100% = 3%
Therefore, the maximum percentage error in the determination of the volume is 3%.
Q2: A dimensionless quantity is constructed in terms of electronic charge e, permittivity of free space ε₀, Planck’s constant h, and speed of light c. If the dimensionless quantity is written as eᵅ ε₀ᵝ hᵞ cᵟ and n is a non-zero integer, then (α, β, γ, δ) is given by:
(a) (2n, −n, −n, −n)
(b) (n, −n, −2n, −n)
(c) (n, −n, −n, −2n)
(d) (2n, −n, −2n, −2n) [JEE Advanced 2024 Paper 1]
Ans: (a)
To find the values of (α, β, γ, δ) for which the expression eαε0βhγcδ is dimensionless, we need to ensure that the product of the quantities has no overall physical dimensions. This means the dimensions of charge (e), permittivity (ε0), Planck's constant (h), and speed of light (c) must cancel each other out.
Electronic charge (e): The dimension of charge in terms of fundamental dimensions is:
[e] = [A.T]
where A represents the dimension of current and T represents time.
Permittivity of free space (ε0): The dimension is given by:
[ε0] = [M-1L-3T4A2]
Planck’s constant (h): The dimension is:
[h] = [M L2T-1]
Speed of light (c): The dimension is:
[c] = [L T-1]
We now write the expression for the dimensionless quantity and set its dimensions to zero:
[eαε0βhγcδ] = [AαTα] [M-βL-3βT4βA2β] [MγL2γT-γ] [LδT-δ]
Combining the dimensions, we get:
[eαε0βhγcδ] = [M-β+γL-3β+2γ+δTα+4β-γ-δAα+2β]
For the quantity to be dimensionless, the exponents of M, L, T, and A must all be zero:
-β + γ = 0
-3β + 2γ + δ = 0
α + 4β - γ - δ = 0
α + 2β = 0
From the fourth equation:
α + 2β = 0 ⟹ α = -2β
Substituting α = -2β into the third equation:
-2β + 4β - γ - δ = 0 ⟹ 2β - γ - δ = 0 ⟹ γ + δ = 2β
From the first equation:
-β + γ = 0 ⟹ γ = β
Substituting γ = β into γ + δ = 2β:
β + δ = 2β ⟹ δ = β
Thus, we have:
α = -2β
γ = β
δ = β
Let β = -n where n is a non-zero integer. Then, we can write the values as:
α = -2(-n) = 2n
β = -n
γ = -n
δ = -n
Hence, the tuple (α, β, γ, δ) is given by: (2n, -n, -n, -n)
So, the correct option is Option A: (2n, -n, -n, -n)
2023
Q1: In an experiment for determination of the focal length of a thin convex lens, the distance of the object from the lens is10 ± 0.1 cmand the distance of its real image from the lens is 20 ± 0.2 cm. The error in the determination of focal length of the lens is n%. The value of nis ______.
[JEE Advanced 2023 Paper 1 ]
Ans: 1
Given :
- Object distance u = 10.0 ± 0.1cm
- Image distance v = 20.0 ± 0.2cm
According to the lens formula for a thin lens :
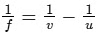
So, we can calculate the focal length :
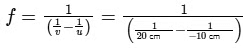
= 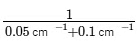
= 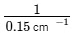 = 20/3 cmNext, we need to calculate the error in the determination of the focal length. For that, we find the differential of the lens formula :
= 20/3 cmNext, we need to calculate the error in the determination of the focal length. For that, we find the differential of the lens formula :
Then, the derivative of the equation gives us the change in the focal length (df)in terms of the changes in the object distance (du)and the image distance (dv):
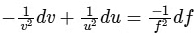
For maximum error, we get :
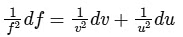
This equation tells us how errors in (u)and vpropagate to an error in f. Now, when you compute the relative error in the focal length, you get :
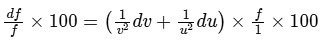
Plugging in your values of u = 10 cm, du = 0.1 cm, v = 20 cm, dv = 0.2 cm, and f = 20/3 cm, you indeed get:
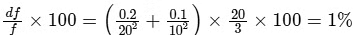
So, the error in the focal length of the lens is indeed 1% (i.e., n = 1).
Q2: Young's modulus of elasticity Yis expressed in terms of three derived quantities, namely, the gravitational constant G, Planck's constant ℎand the speed of light c, as Y = CαℎβGγ. Which of the following is the correct option?
(a) α = 7, β = -1, γ = -2
(b) α = -7, β = -1, γ = -2
(c) α = 7, β = -1, γ = 2
(d) α = -7, β = 1, γ = -2 [JEE Advanced 2023 Paper 2 ]
Ans:(a)
Given the equation, Y = CαℎβGγ
where Y represents Young's modulus, c the speed of light, h is Planck's constant, G is the gravitational constant, and α, β, and γ are powers to be determined.
We start by expressing the quantities involved in terms of their fundamental dimensions: Mass (M), Length (L), and Time (T). The equation in terms of dimensions is :
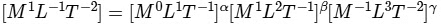
Next, by equating the powers of the dimensions M, L, and T on both sides of the equation, we form three separate equations:
1. Equating the powers of M, we get : β − γ = 1
2. Equating the powers of L, we get : α + 2β + 3γ= −1
3. Equating the powers of T, we get : −α − β− 2γ = −2
Now we can solve this system of equations.
From the first equation, we get β = γ + 1.
Substituting βfrom the first equation into the second and third equations, we get :
For the second equation, substituting βwe get : α + 2(γ + 1) + 3γ = −1, which simplifies to
α = −5γ − 3.
For the third equation, substituting βwe get : −α − (γ + 1)−2γ = −2, which simplifies to α = −3γ − 1.
Setting the two equations for αequal to each other gives : −5γ − 3 = −3γ − 1, which simplifies to γ = −2.
Substituting γ = −2back into the equations for αand βwe find γ = 7 and β = −1.
So, the solution to the system is α = 7,β = −1,γ = −2, which corresponds to Option A.
2022
Q1: In a particular system of units, a physical quantity can be expressed in terms of the electric charge e, electron mass me, Planck's constant ℎ, and Coulomb's constant
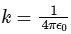 , where ε0is the permittivity of vacuum. In terms of these physical constants, the dimension of the magnetic field is
, where ε0is the permittivity of vacuum. In terms of these physical constants, the dimension of the magnetic field is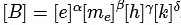 . The value of α + β + γ + ∂is _______. [JEE Advanced 2022 Paper 2 ]
. The value of α + β + γ + ∂is _______. [JEE Advanced 2022 Paper 2 ]Ans: 4
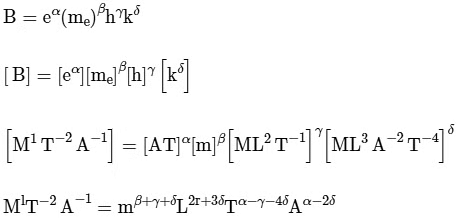
Compare: 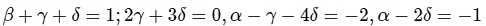
On solving: α = 3, β = 2, γ = -3, ∂ = 2So, α + β + γ + ∂ = 4
Q2: Area of the cross-section of a wire is measured using a screw gauge. The pitch of the main scale is 0.5 mm. The circular scale has 100 divisions and for one full rotation of the circular scale, the main scale shifts by two divisions. The measured readings are listed below.
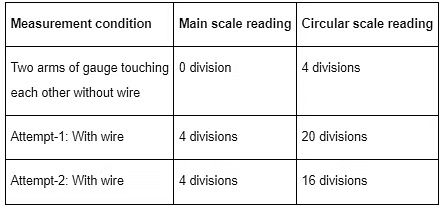
What are the diameter and cross-sectional area of the wire measured using the screw gauge?
(a) 2.22 ± 0.02 mm,π(1.23 ± 0.02)mm2
(b) 2.22 ± 0.01 mm,π(1.23 ± 0.01)mm2
(c) 2.14 ± 0.02 mm, π(1.14 ± 0.02)mm2
(d) 2.14 ± 0.01 mm,π(1.14 ± 0.01)mm2 [JEE Advanced 2022 Paper 2 ]
Ans: (c)
LC = 0.1/100 = 0.001 mm
Zero error = 4 x 0.001 = 0.004 mm
Reading 1 = 0.5 x 4 + 20 x 0.001 - 0.004 = 2.16 mm
Reading 2 = 0.5 x 4 + 16 x 0.001 - 0.004 = 2.12mm
Mean value = 2.14 mm
Mean absolute error = 
Diameter = 2.14 ± 0.02Area = π / 4 d2
2021
Q1: The smallest division on the main scale of a Vernier calipers is 0.1 cm. Ten divisions of the Vernier scale correspond to nine divisions of the main scale. The figure below on the left shows the reading of this calipers with no gap between its two jaws. The figure on the right shows the reading with a solid sphere held between the jaws. The correct diameter of the sphere is
(a) 3.07 cm
(b) 3.11 cm
(c) 3.15 cm
(d) 3.17 cm [JEE Advanced 2021 Paper 1 Online]
Ans:(c)
Least count of Vernier calipers (L.C) = (1 - 9/10)0.1 =0.01 cm
We know that main scale reading (MSR) is the first reading on the main scale immediately to the left of the zero of the Vernier scale. But there are no marks on the main scale before zero of the Vernier scale. We claim that MSR = −0.1 cm. The Vernier scale reading is VSR = 6 and the least count is LC = 0.01 cm.
Substitute these values to get,
Zero Error = MSR + VSR × LC
= -0.1 + 6 × 0.01 = -0.04 cm
Now in the second figure, the reading from main scale is 3.1 cm will be added to 1st matching division of vernier so,
Reading = 3.1 cm + 1 × L.C
= 3.1 cm + 0.01
= 3.11 cm
So correct diameter of the sphere
= 3.11 - (Zero Error)
= (3.11 + 0.04) cm
= 3.15 cm
Q2:A physical quantity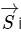 is defined as
is defined as 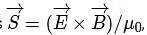 where
where 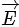 is electric field,
is electric field, 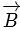 is magnetic field and μ0is the permeability of free space. The dimensions of
is magnetic field and μ0is the permeability of free space. The dimensions of 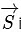 are the same as the dimensions of which of the following quantity(ies)?
are the same as the dimensions of which of the following quantity(ies)?
(a) Energy / Charge x Current
(b) Force / Length x Time
(c) Energy / Volume
(d) Power / Area [JEE Advanced 2021 Paper 2]
Ans: (b) & (d)
Dimension of electric field 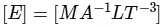
Dimensions of magnetic field [B]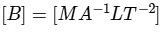
Dimensions of magnetic permeability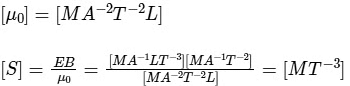
2020
Q1: Sometimes it is convenient to construct a system of units so that all quantities can be expressed in terms of only one physical quantity. In one such system, dimensions of different quantities are given in terms of a quantity X as follows: [position] = [Xα]; [speed] = [Xβ]; [acceleration] = [Xp]; [linear momentum] = [Xq]; [force] = [Xr]. Then
Ans: (a) & (b)
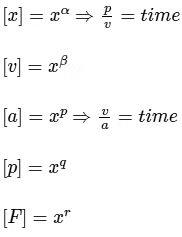
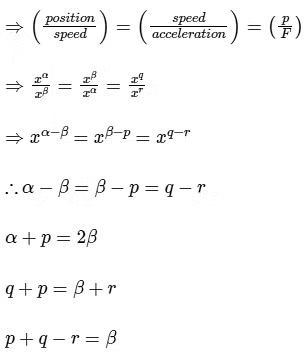
2019
Q1: An optical bench has 1.5 m long scale having four equal divisions in each cm. While measuring the focal length of a convex lens, the lens is kept at 75 cm mark of the scale and the object pin is kept at 45 cm mark. The image of the object pin on the other side of the lens overlaps with image pin that is kept at 135 cm mark. In this experiment, the percentage error in the measurement of the focal length of the lens is .............. [JEE Advanced 2019 Paper 2 ]
Ans:1.38
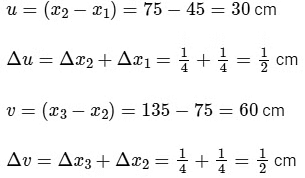
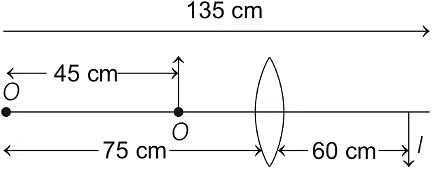
∴ 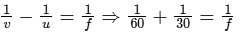
∴ f = 20 cm Also,
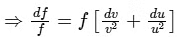
= 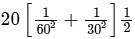
∴ 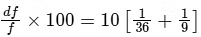
= 50/36
= 1.38 and 1.39 (both)
Q2: Let us consider a system of units in which mass and angular momentum are dimensionless. If length has dimension of L, which of the following statement(s) is/are correct?
(a) The dimension of force is [L]-3
(b) The dimension of power is [L]-5
(c) The dimension of energy is [L]-2
(d) The dimension of linear momentum is [L]-1 [JEE Advanced 2019 Paper 1]
Ans: (a), (c) & (d)
[M] = [Mass] = [M0L0T0]
[J] = [Angular momentum] = [ML2T-1]
[L] = [Length]
Now, [ML2T-1] = [M0L0T0]
∴[L2] = [T]
Power [P] = [MLT2.LT-1] = [ML2T-3]
= [L2L-6]
[P] = [L-4]
Energy/Work [W] = [MLT-2.L]
= [L2L-4] = [L-2]
Force [F] = [MLT-2] = [L.L-4] = [L-3]
Linear momentum [p] = [MLT-1] = [L.L-2]
[p] = [L-1]
2018
Q1: A steel wire of diameter 0.5 mm and Young's modulus 2 × 1011Nm−2 carries a load of mass M. The length of the wire with the load is 1.0 m. A vernier scale with 10 divisions is attached to the end of this wire. Next to the steel wire is a reference wire to which a main scale, of least count 1.0 mm , is attached. The 10 divisions of the vernier scale correspond to 9 divisions of the main scale. Initially, the zero of vernier scale coincides with the zero of main scale. If the load on the steel wire is increased by 1.2 kg, the vernier scale division which coincides with a main scale division is _____________. Take g = 10ms−2. and π = 3.2. [JEE Advanced 2018 Paper 2 ]
Ans: 3
We know that
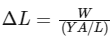
where W is weight or load = mg = 1.2 ×10 = 12 kg m s−2, Y is Young's modulus = 2 ×1011N m−2, L is length of wire with load = 1.0 m, A is area of steel wire = 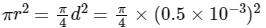
Therefore,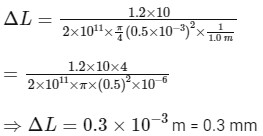
Now, least count of vernier scale = (1 - 9/10)mm = 0.1 mm
Therefore, Vernier reading = ΔL / Least count
Vernier reading = 0.3 mm / 0.1 mm
= 3
Therefore, 3rdvernier scale division coincides with the main scale division.
Q2: In electromagnetic theory, the electric and magnetic phenomena are related to each other. Therefore, the dimensions of electric and magnetic quantities must also be related to each other. In the questions below, [E]and [B]stand for dimensions of electric and magnetic fields respectively, while [ε0]and [μ0]stand for dimensions of the permittivity and permeability of free space respectively. [L]and [T]are dimensions of length and time respectively. All the quantities are given in SI units.
The relation between [ε0]and [μ0]is [JEE Advanced 2018 Paper 1 ]
(a) 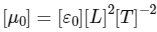
(b) 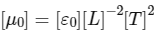
(c) 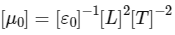
(d) 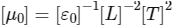
Ans:(d)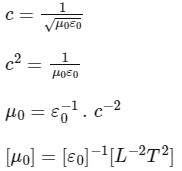
|
291 videos|648 docs|183 tests
|
FAQs on JEE Advanced Previous Year Questions (2018 - 2024): Units & Measurements - Physics for JEE Main & Advanced
| 1. What are the key topics covered in the Units & Measurements section of JEE Advanced? |  |
| 2. How can I effectively prepare for the Units & Measurements topic in JEE Advanced? |  |
| 3. What types of questions can I expect from the Units & Measurements section in JEE Advanced? |  |
| 4. Are there any common mistakes to avoid while preparing for Units & Measurements in JEE Advanced? |  |
| 5. How important is the Units & Measurements section for scoring in JEE Advanced? |  |






















