JEE Advanced Previous Year Questions (2018 - 2024): Chemical Kinetics | Chemistry for JEE Main & Advanced PDF Download
2024
Q1: A sample initially contains only U-238 isotope of uranium. With time, some of the U-238 radioactively decays into Pb-206 while the rest of it remains undisintegrated.When the age of the sample is P × 10⁸ years, the ratio of mass of Pb-206 to that of U-238 in the sample is found to be 7. The value of P is ______.
[Given: Half-life of U-238 is 4.5 × 10⁹ years; logₑ 2 = 0.693] [JEE Advanced 2024 Paper 2]
Ans: 143
Given Data:
Ratio of mass of Pb206 to U238 = 71
Mass of Pb206 = 7 g
Mass of U238 = 1 g
Half-life of U238 = 4.5 × 10⁹ years
log₂ 2 = 0.693
Calculate Moles:
Moles of Pb206:
Moles of Pb206 = 7206 = 34 × 10⁻³ moles
Moles of U238:
Moles of U238 = 1238 = 4.2 × 10⁻³ moles
Initial Moles of U238 (N₀):
N₀ = Moles of U238 initially = Moles of Pb206 + Moles of remaining U238
N₀ = 34 × 10⁻³ + 4.2 × 10⁻³ = 38.2 × 10⁻³ moles
Calculate the Time:
Using the decay formula:
λt = ln N₀Nₜ
Where λ (decay constant):
λ = ln 2t1/2 = 0.6934.5 × 10⁹ years
Calculate ln N₀Nₜ:
ln N₀Nₜ = ln 38.24.2 = ln 9.09
Simplify ln 9.09:
ln 9.09 ≈ 2.21
Plug in the Values:
t = 4.5 × 10⁹ years0.693 × ln 9.09
t = 4.5 × 10⁹ years × 2.210.693
t ≈ 4.5 × 10⁹ × 3.184 ≈ 14.33 × 10⁹ years
Convert to P × 10⁸:
t = P × 10⁸ years
P × 10⁸ = 14.33 × 10⁹
P = 143.28
Thus, the value of P is 143.28.
Q2: Consider the following reaction,
2H2(g) + 2NO(g) → N2(g) + 2H2O(g)
which follows the mechanism given below:
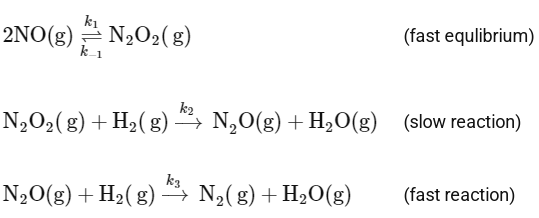 [JEE Advanced 2024 Paper 1]
[JEE Advanced 2024 Paper 1]
Ans: 3
The given reaction is:
2H2(g) + 2NO(g) → N2(g) + 2H2O(g)
And it follows the mechanism below: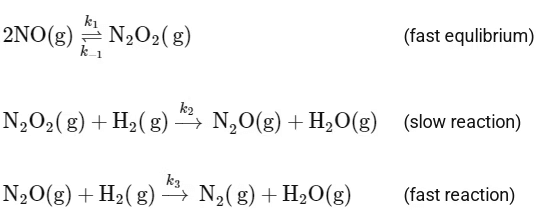
To determine the order of the reaction, we need to focus on the slow step, as it is the rate-determining step. The slow step is: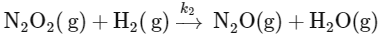
The rate law for this step can be written as:
Rate = k2[N2O2][H2]
However, [N2O2] is an intermediate and its concentration can be expressed in terms of the reactants. From the fast equilibrium step:
2NO(g) ⇌ N2O2(g)
The equilibrium constant for this step can be written as:
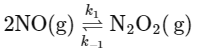
Hence, the concentration of the intermediate N2O2 can be expressed as:
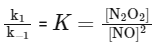
Substituting this into the rate law for the slow step gives:
Rate = k2 K [NO]2 [H2]
Let's combine k2 and K into a single constant, say k':
Rate = k' [NO]2 [H2]
This implies that the reaction is second-order in NO and first-order in H2. Therefore, the overall order of the reaction is:
2 + 1 = 3
Thus, the order of the reaction is 3.
2022
Q1: Match the rate expressions in LIST-I for the decomposition of X with the corresponding profiles provided in LIST-II. Xs and k are constants having appropriate units. [JEE Advanced 2022 Paper 1]
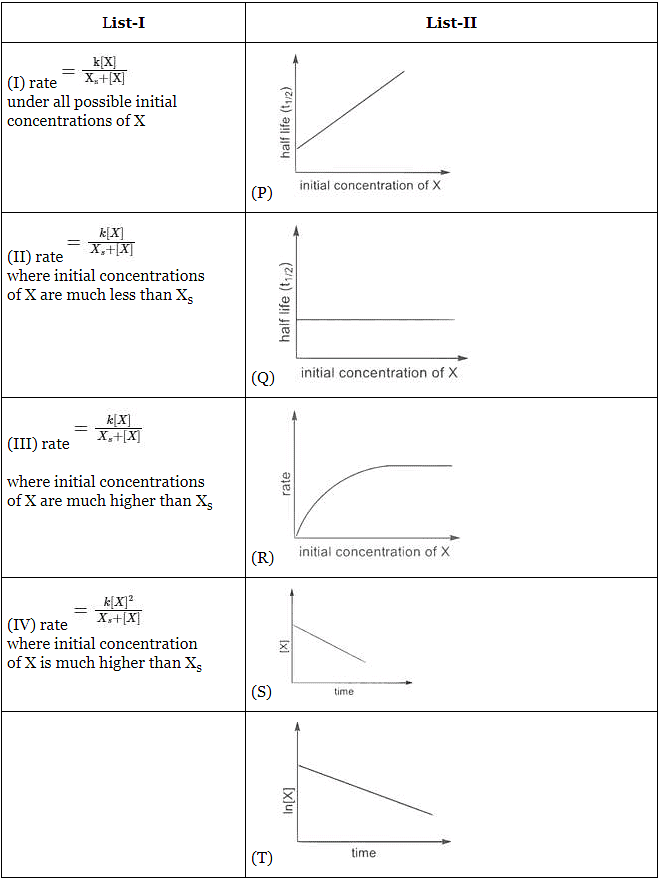 (a) I → P ; II → Q; III → S ; IV → T
(a) I → P ; II → Q; III → S ; IV → T
(b) I → R ; II → S ; III → S ; IV → T
(c) I → P ; II → Q; III → Q; IV → R
(d) I → R ; II → S ; III → Q; IV → R
Ans: (a)
In this case curve-R given in List-II will match.
∴ I → P, Q, R, S, T (The graph of half-life should start from origin)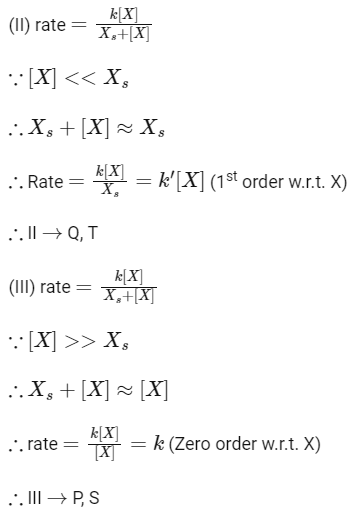
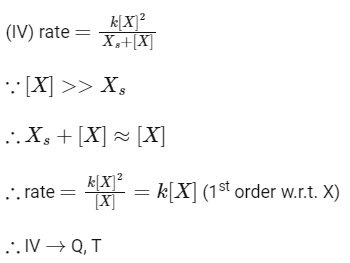
2021
Q1: For the following reaction, 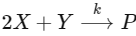 the rate of reaction is
the rate of reaction is 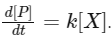
Two moles of X are mixed with one mole of Y to make 1.0 L of solution. At 50 s, 0.5 mole of Y is left in the reaction mixture. The correct statement(s) about the reaction is(are)
(Use : ln 2 = 0.693) [JEE Advanced 2021 Paper 2]
(a) A The rate constant, k, of the reaction is 13.86 × 10−4 s−1
(b) Half-life of X is 50 s.
(c) At 50 s, 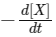 = 13.86 × 10−3 mol L−1 s−1.
= 13.86 × 10−3 mol L−1 s−1.
(d) At 100 s, 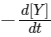 = 3.46 × 10−3 mol L−1 s−1.
= 3.46 × 10−3 mol L−1 s−1.
Ans: (b, c, d)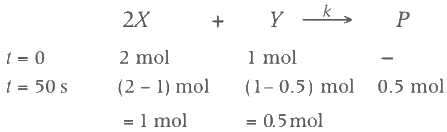
As the concentration of reactant becomes half at t = 50 s. So, half-time of reaction is 50 s.
Given,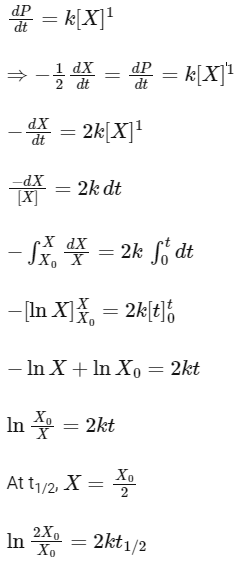
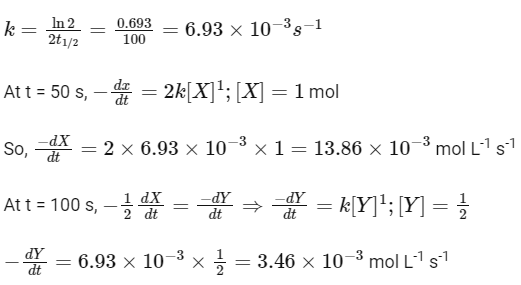
So, options (b), (c) and (d) are correct.
2020
Q1: 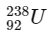 is known to undergo radioactive decay to form
is known to undergo radioactive decay to form  by emitting alpha and beta particles. A rock initially contained 68 x 10-6 g of
by emitting alpha and beta particles. A rock initially contained 68 x 10-6 g of 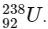 If the number of alpha particles that it would emit during its radioactive decay of
If the number of alpha particles that it would emit during its radioactive decay of 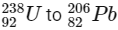 in three half-lives is Z × 1018, then what is the value of Z? [JEE Advanced 2020 Paper 1]
in three half-lives is Z × 1018, then what is the value of Z? [JEE Advanced 2020 Paper 1]
Ans: 1.2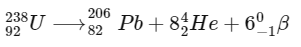
Number of moles of 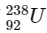 present initially
present initially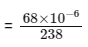
After three half-lifes, moles of 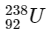 decayed
decayed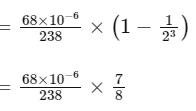
Therefore, number of α-particles emitted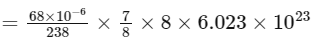
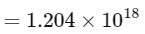
≈ 1.2 × 1018
Thus, the correct answer is 1.2.
Q2: Which of the following plots is(are) correct for the given reaction?
([P]0 is the initial concentration of P) [JEE Advanced 2020 Paper 2]
(a)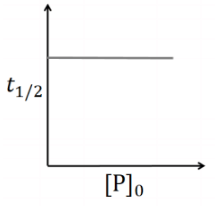
(b)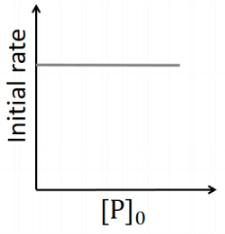
(c)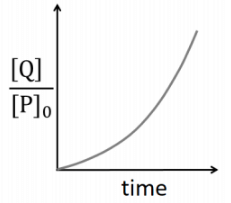
(d)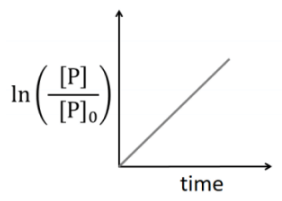
Ans: (a)
This is first order reaction and for first order reaction 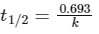
So, half-life is independent of initial concentration.
Therefore, the plot (a) correct.
For first order reaction,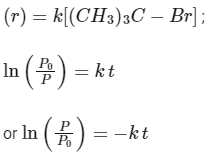
Hence, plot (b) and (d) are incorrect. For first order reaction,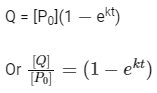
Hence, plot (c) is incorrect.
2019
Q1: The decomposition reaction 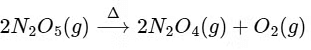 is started in a closed cylinder under isothermal isochoric condition at an initial pressure of 1 atm. After Y × 103 s, the pressure inside the cylinder is found to be 1.45 atm. If the rate constant of the reaction is 5 × 10-4s-1, assuming ideal gas behaviour, the value of Y is ............... [JEE Advanced 2019 Paper 2]
is started in a closed cylinder under isothermal isochoric condition at an initial pressure of 1 atm. After Y × 103 s, the pressure inside the cylinder is found to be 1.45 atm. If the rate constant of the reaction is 5 × 10-4s-1, assuming ideal gas behaviour, the value of Y is ............... [JEE Advanced 2019 Paper 2]
Ans: 2.3
At constant V, T
At initial t = 0 and final t = y × 103 sec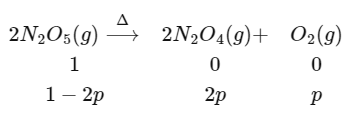
pTotal = 1 − 2p + 2p + p
1.4 = 1 + p
p = 0.45 atm
According to first order reaction,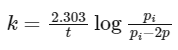
pi = 1 atm (given)
2p = 2 × 0.45 = 0.9 atm
On substituting the values in above equation,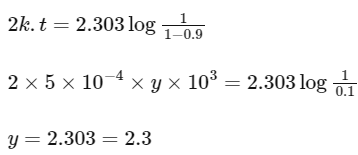
Note : Unit of rate constant (k), i.e. s−1 represents that it is a first order reaction.
Q2: Consider the kinetic data given in the following table for the reaction A + B + C → Product.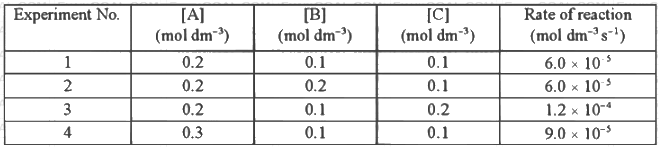
The rate of the reaction for [A] = 0.15 mol dm-3, [B] = 0.25 mol dm-3 and [C] = 0.15 mol dm-3 is found to be Y × 10-5 mol dm-3s-1. The value of Y is _______ [JEE Advanced 2019 Paper 1]
Ans: 6.75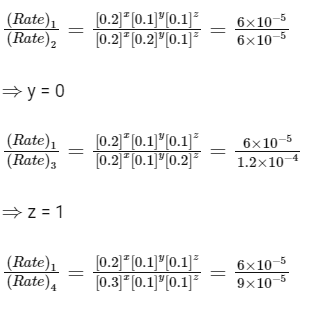
⇒ x = 1
So, rate = k[A]1[C]1
From exp-Ist,
Rate = 6.0 × 10−5 mol dm−3 s−1
6.0 × 10−5 = k[0.2]1[0.1]1
k = 3 × 10−3
Given, [A] = 0.15 mol dm−3
[B] = 0.25 mol dm−3
[C] = 0.15 mol dm−3
∴ Rate = (3 × 10−3) × [0.15]1[0.25]0[0.15]1
= 3 × 10−3 × 0.15 × 0.15
Rate = 6.75 × 10−5 mol dm−3 s−1
Thus, Y = 6.75
Q3: In the decay sequence.
x1, x2, x3 and x4 are particles/radiation emitted by the respective isotopes. The correct option(s) is(are) [JEE Advanced 2019 Paper 1]
(a) Z is an isotope of uranium
(b) x2 is β-
(c) x1 will deflect towards negatively charged plate
(d) x3 is γ -ray
Ans: (a, b, c)
In decay sequence,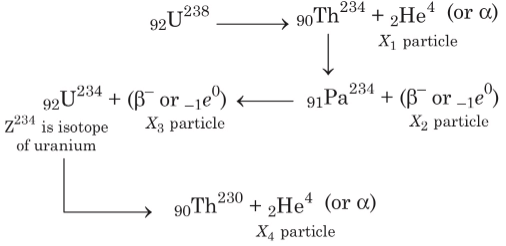
X1 particle will deflect towards negatively charged plate due to presence of positive charge on α - particles.
Hence, options (a, b, c) are correct.
2018
Q1: Consider the following reversible reaction, A (g) + B (g) → AB (g).
The activation energy of the backward reaction exceeds that of the forward reaction by 2RT (in J mol −1). If the pre-exponential factor of the forward reaction is 4 times that of the reverse reaction, the absolute value of ΔG∘ (in J mol−1) for the reaction at 300 K is ____________.
(Given; ln (2) = 0.7 , RT = 2500 J mol−1 at 300 K and G is the Gibbs energy) [JEE Advanced 2018 Paper 2]
Ans: 8500
At 300 K ,
For the reversible reaction,
A (g) + B (g) ⇌ AB (g)
(i) Pre-exponential factor for forward reaction (Af) = 4 × pre-exponential factor for backward reverse reaction (Ab)
Af = 4 × Ab
(ii) Activation energy for backward reaction (Eb)f − Activation energy = 2 RT for forward reaction (Ea)f- Ab − Af = 2 RT
(iii) Equilibrium constant 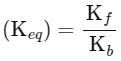
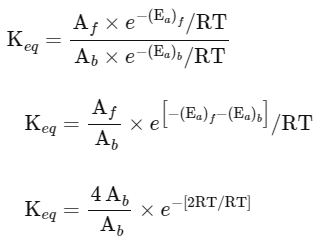
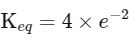
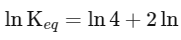
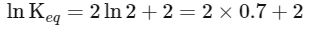
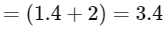
The expression for the change in Gibbs free energy of reaction (ΔG) is given as:
ΔG = ΔG∘ + RT ln k
At equilibrium, ΔG = 0
ΔG∘ = − RT ln Keq
Substituting the value of RT and ln Keq
ΔG∘ = − 2500 J mol−1 × 3.4
ΔG∘ = − 8500 J mol−1
The absolute value of Gibbs free energy (ΔG∘) for the reaction at 300 K is 8500 J mol−1.
Q2: For a first order reaction A (g) → 2B(g) + C(g) at constant volume and 300 K , the total pressure at the beginning (t = 0) and at time t are P0 and P1 , respectively. Initially, only A is present with concentration [A]0 , and t1/3 is the time required for the partial pressure of A to reach 1/3rd of its initial value. The correct option(s) is (are) (Assume that all these gases behave as ideal gases) [JEE Advanced 2018 Paper 2]
(a)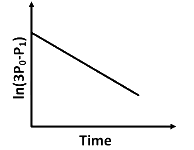
(b)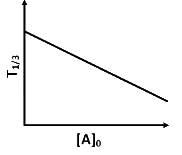
(c)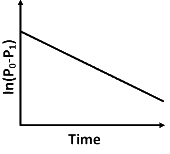
(d)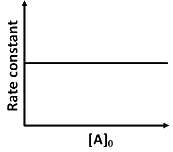
Ans: (a, d)
Total pressure of gaseous mixture at beginning (T = 0) = P0
Total pressure of gaseous mixture after time t (T = t) = Pt
Initial concentration of A = [A]0
Temperature of the reaction mixture (T) = 300 K
For the first order reaction,
Total pressure after time (T = t) = P0 − P + 2P + P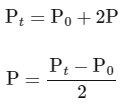
According to integrated rate law for the first order reaction: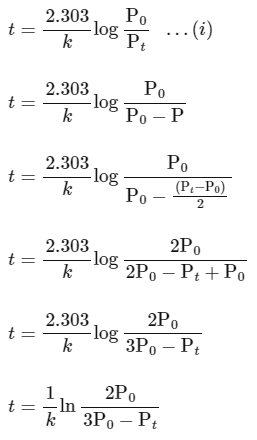
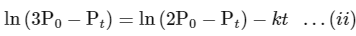
Comparing equation (ii) with equation of straight option line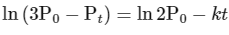
y = c + mx
Plot of ln (3 P0 − P) verses time (t) is represented as: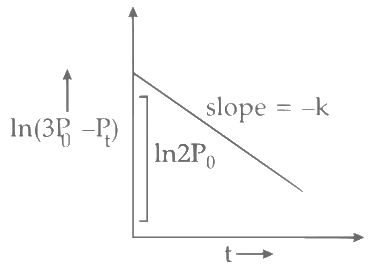 Option (A) is correct.
Option (A) is correct.
(ii) For the first order reaction,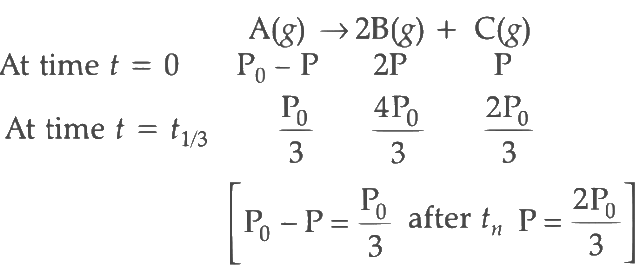
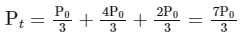
Substituting the value of Pt in eq (i)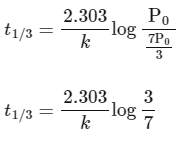
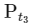 is independent of concentration of (A).
is independent of concentration of (A).
Option (B) is not correct.
(iii) At any time t , rate constant (k) is independent of concentration of [A].
For example: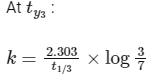
Hence, Option (D) is correct.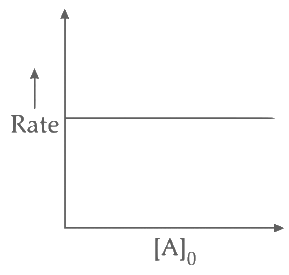
|
366 videos|824 docs|301 tests
|
FAQs on JEE Advanced Previous Year Questions (2018 - 2024): Chemical Kinetics - Chemistry for JEE Main & Advanced
| 1. What is the rate law and how is it determined in chemical kinetics? |  |
| 2. What factors affect the rate of a chemical reaction? |  |
| 3. What is the difference between zero-order, first-order, and second-order reactions? |  |
| 4. How do catalysts influence the activation energy of a reaction? |  |
| 5. What is the Arrhenius equation and what does it represent? |  |





















