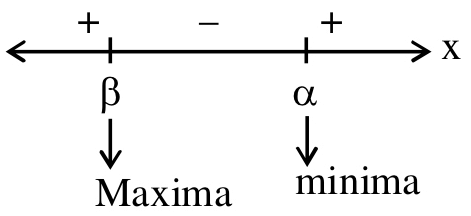
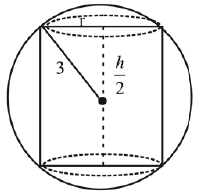
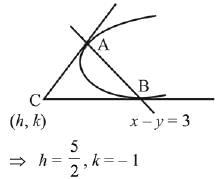
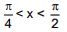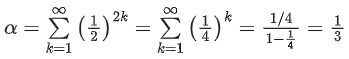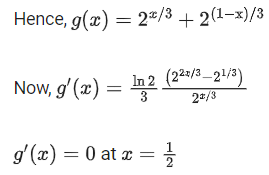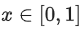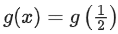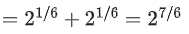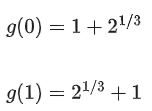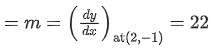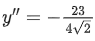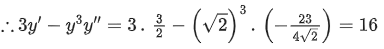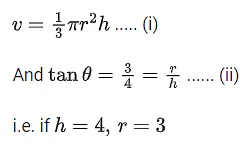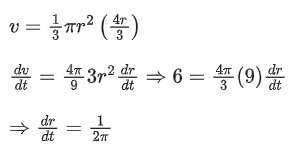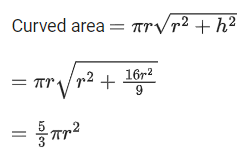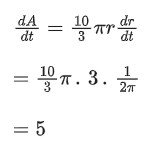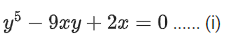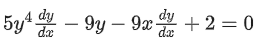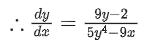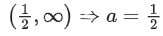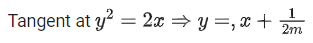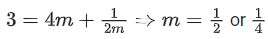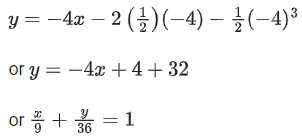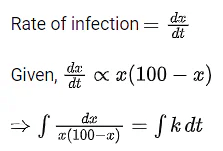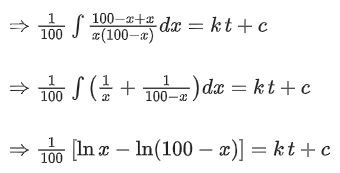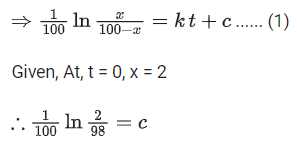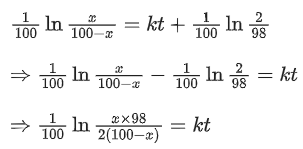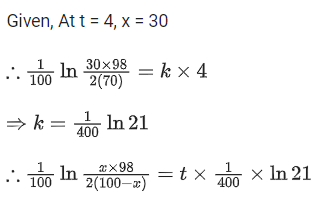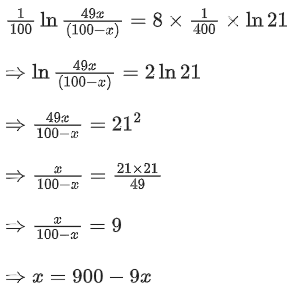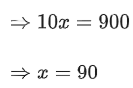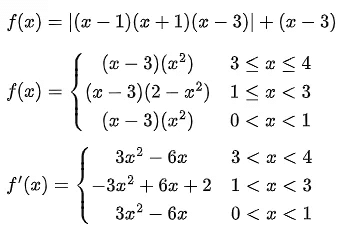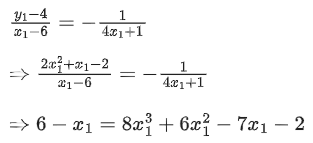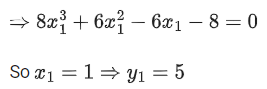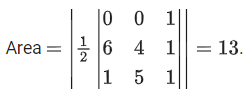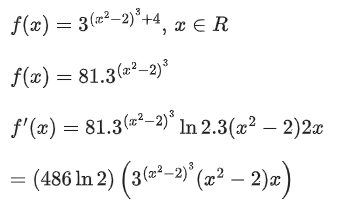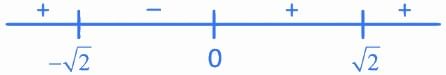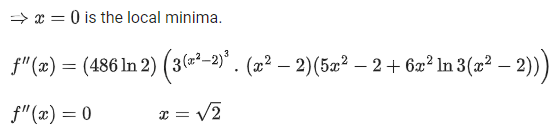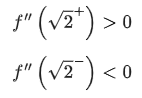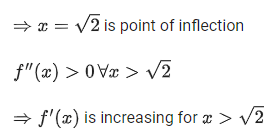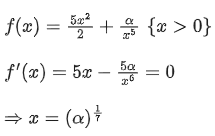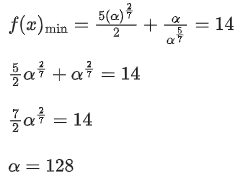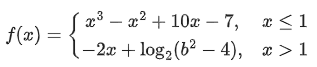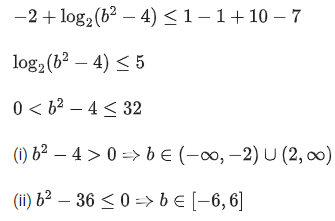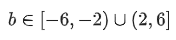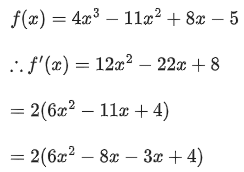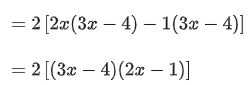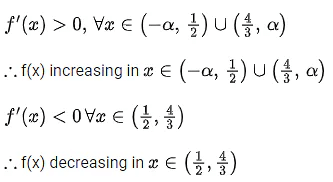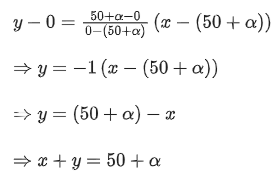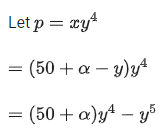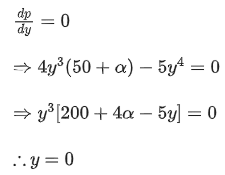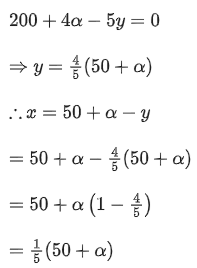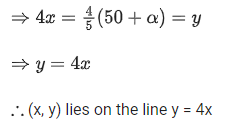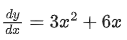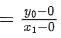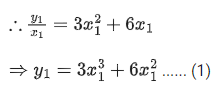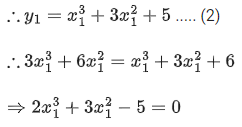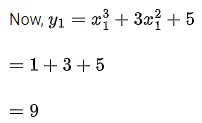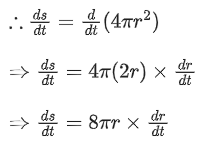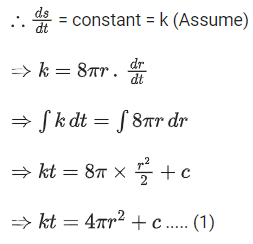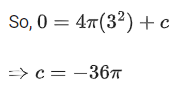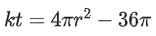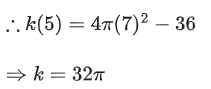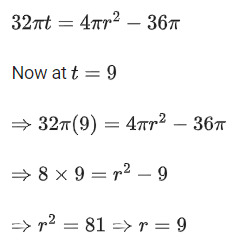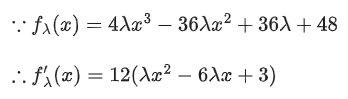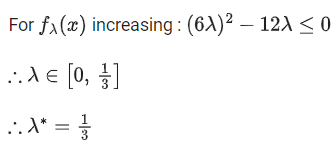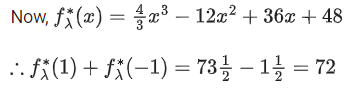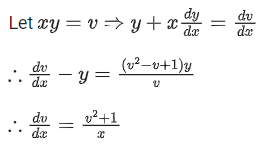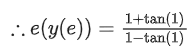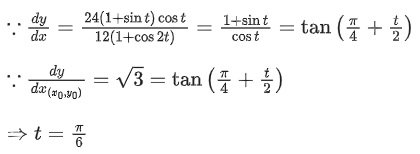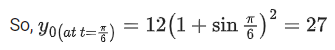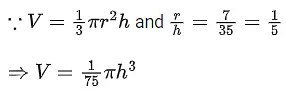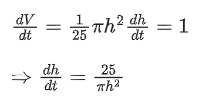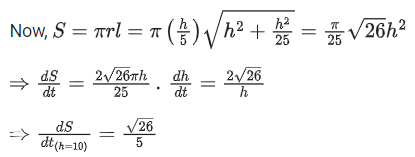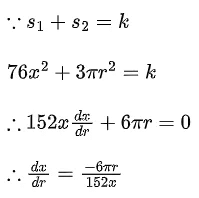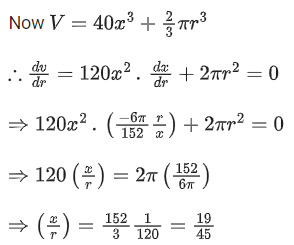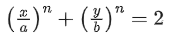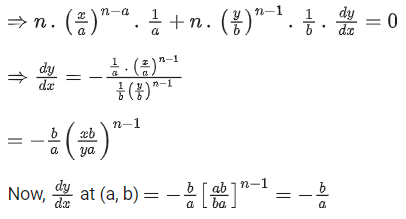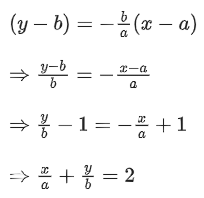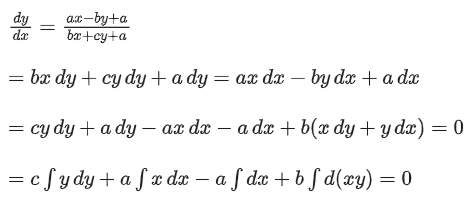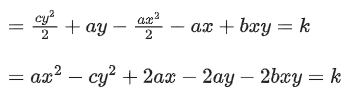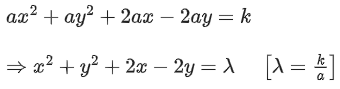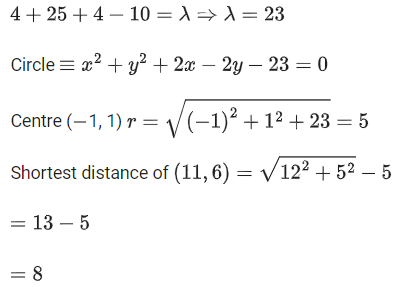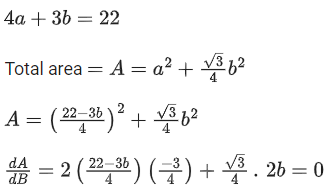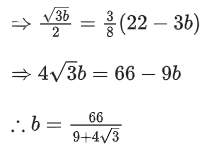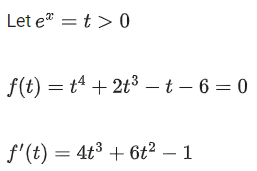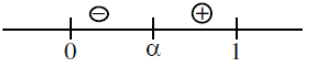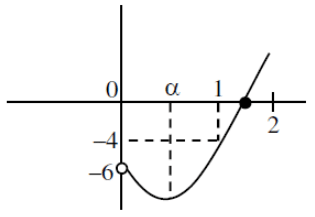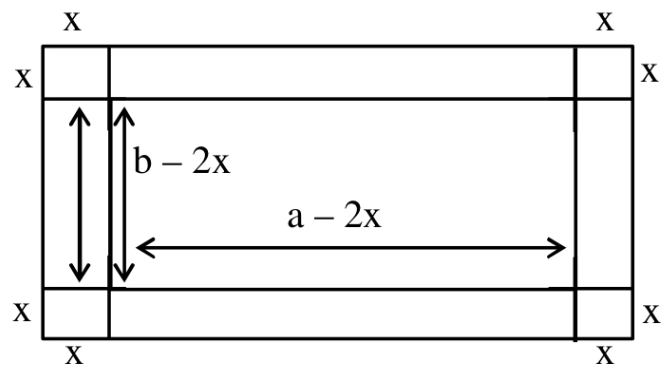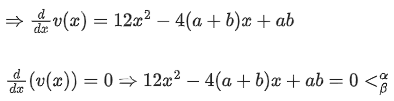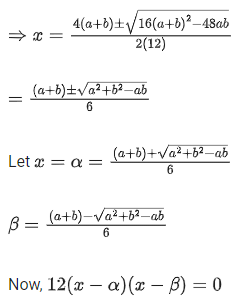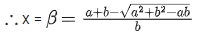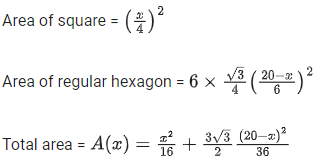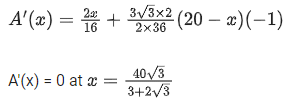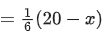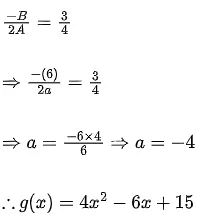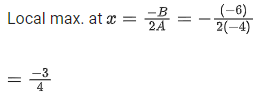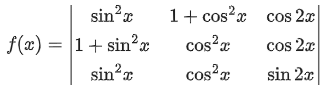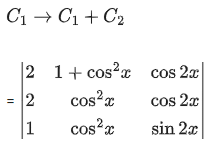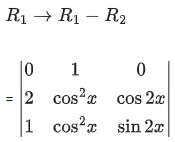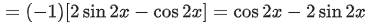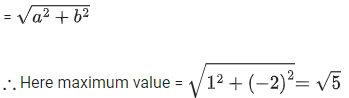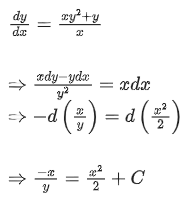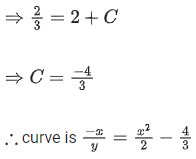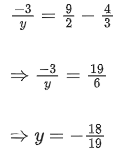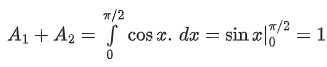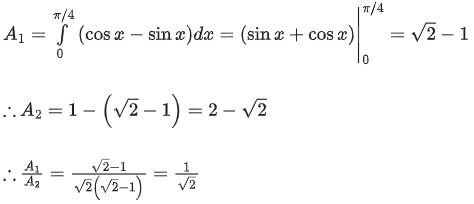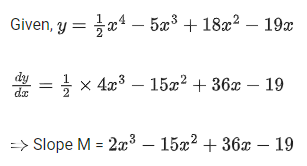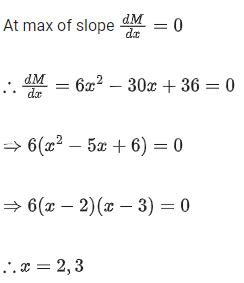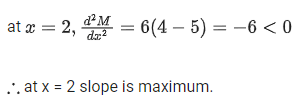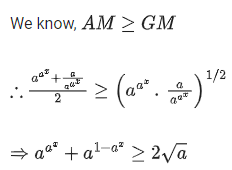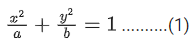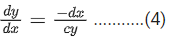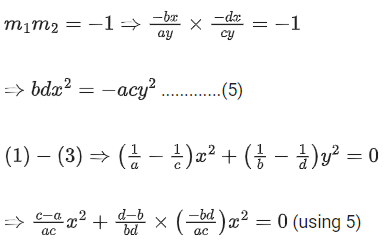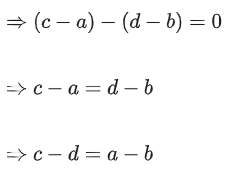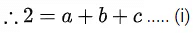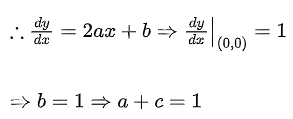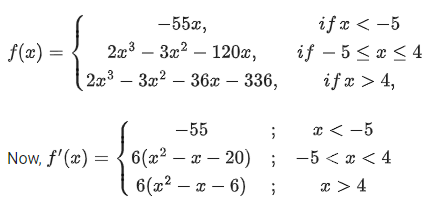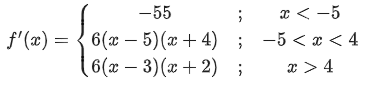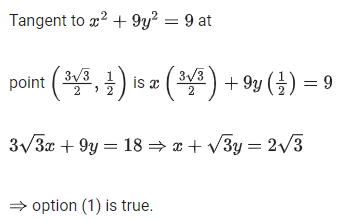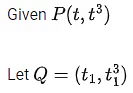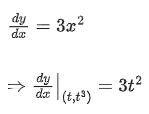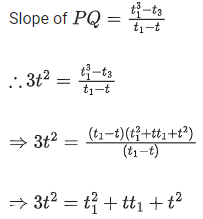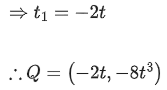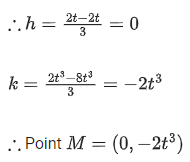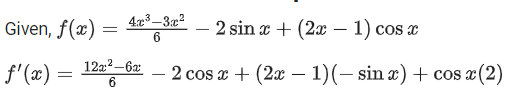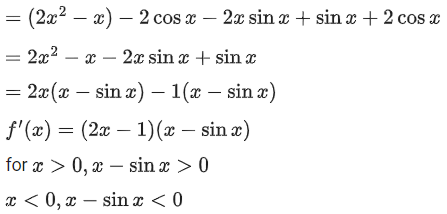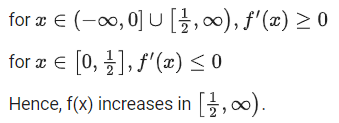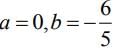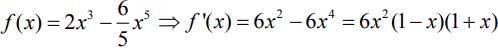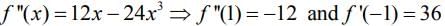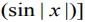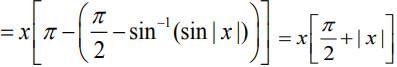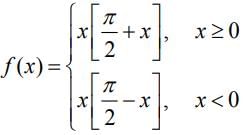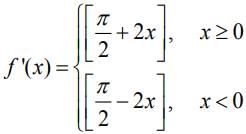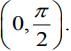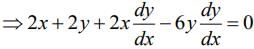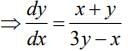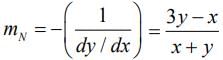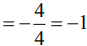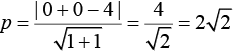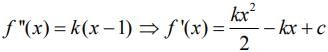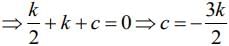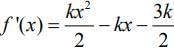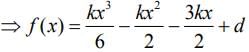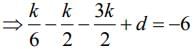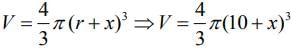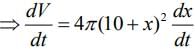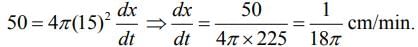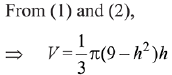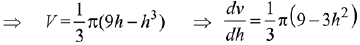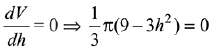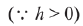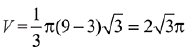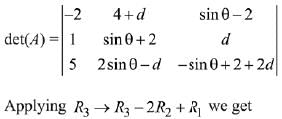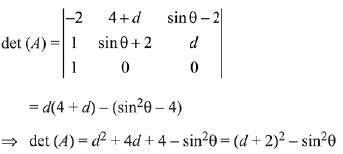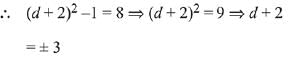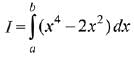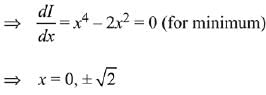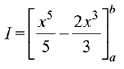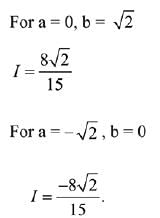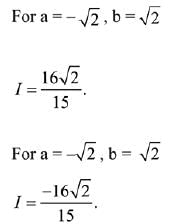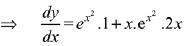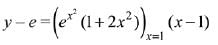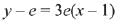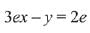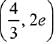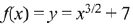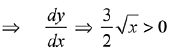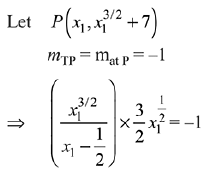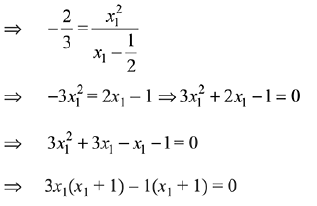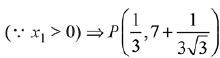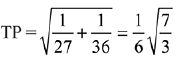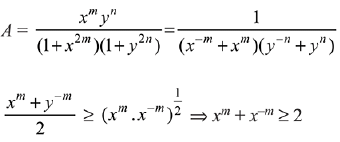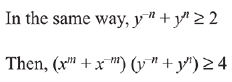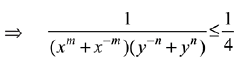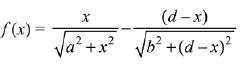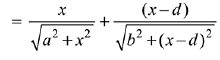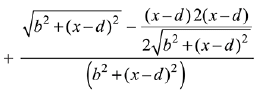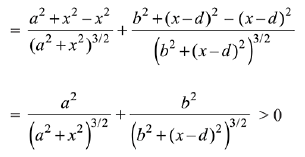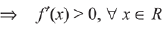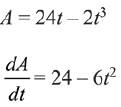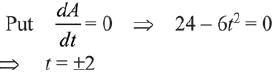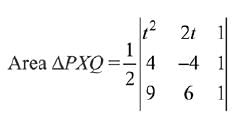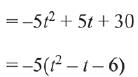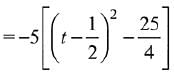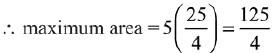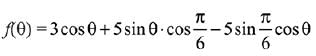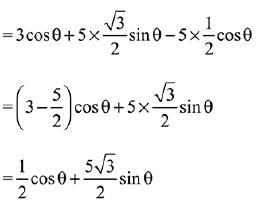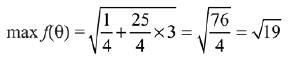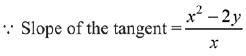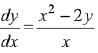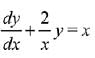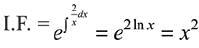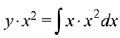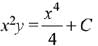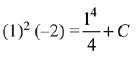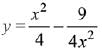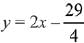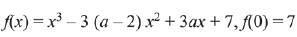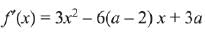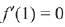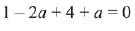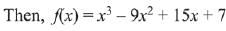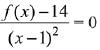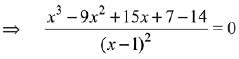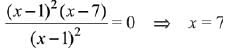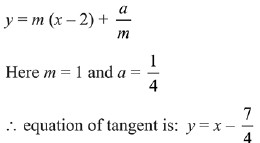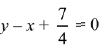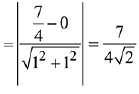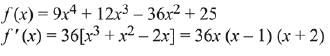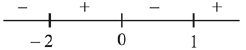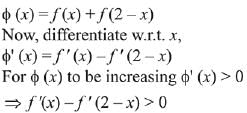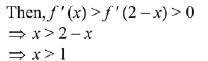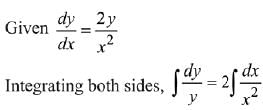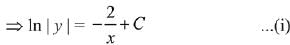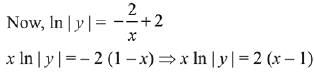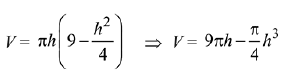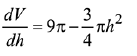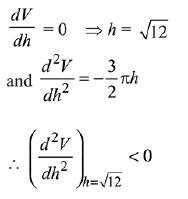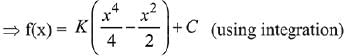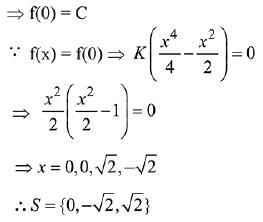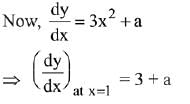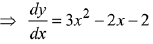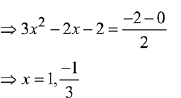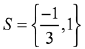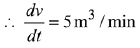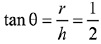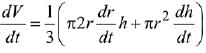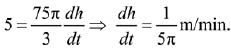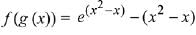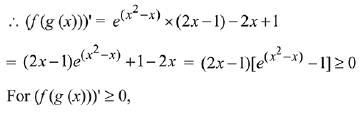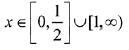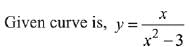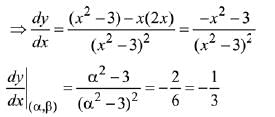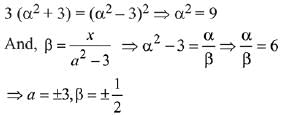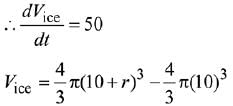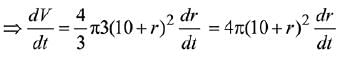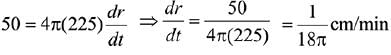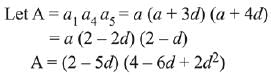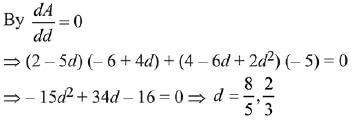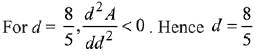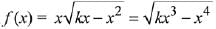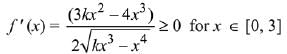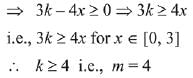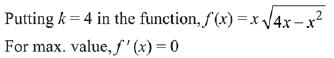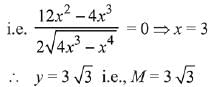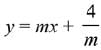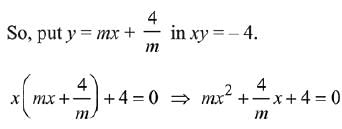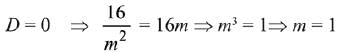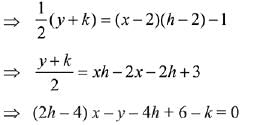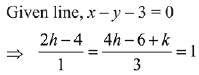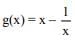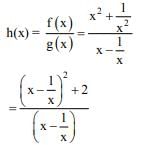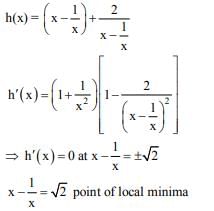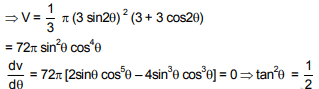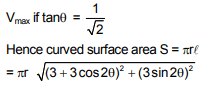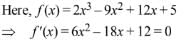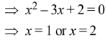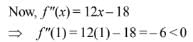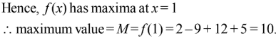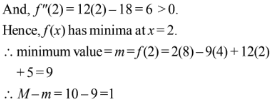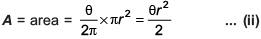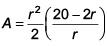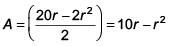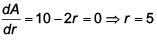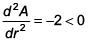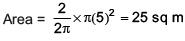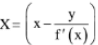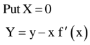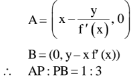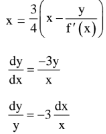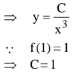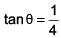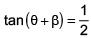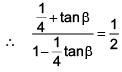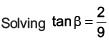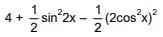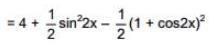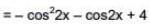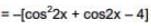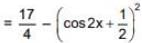Q.1. Let 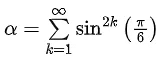
let  be the function defined by
be the function defined by 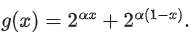
Then, which of the following statements is/are TRUE ? (JEE Advance 2022)
(a) The minimum value of g(x) is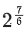
(b) The maximum value of g(x) is 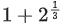
(c) The function g(x) attains its maximum at more than one point
(d) The function g(x) attains its minimum at more than one point
Ans. (a,b,c)
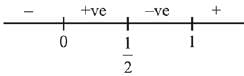
And, derivative changes sign from negative to positive at x = 1/2, hence x = 1/2 is point of local minimum as well as absolute minimum of g(x) for
Hence, minimum value of
Maximum value of g(x) is either equal to g(0) or g(1).
Hence (B) and (C) are also correct
Q. 2. If the tangent to the curve y=x3−x2+x at the point (a,b) is also tangent to the curve y=5x2+2x−25 at the point (2, −1), then |2a+9b| is equal to __________. (JEE Main 2022)
Ans. 195
Slope of tangent to curve y=5x2+2x−25∴ Equation of tangent :y+1 = 22(x−2)
∴ y=22x−45.
Slope of tangent to y=x3−x2+x at point (a,b)
=3a2−2a+1
3a2−2a+1=22
3a2−2a−21=0
∴ a=3 or −73
Also b=a3−a2+a
Then (a,b)=(3,21) or (−7/3,−151/9).
(−7/3,−151/9) does not satisfy the equation of tangent
∴a=3,b=21
∴|2a+9b|=195
Q.3. For the curve C:(x2+y2−3)+(x2−y2−1)5=0, the value of 3y′−y3y′′, at the point (α,α), α>0, on C, is equal to ____________. (JEE Main 2022)
Ans. 16
∵ C:(x2+y2−3)+(x2−y2−1)5=0 for point (α, α)
α2+α2−3+(α2−α2−1)5=0
∴ α=2
On differentiating (x2+y2−3)+(x2−y2−1)5=0 we get
x+yy′+5(x2−y2−1)4(x−yy′)=0 ...... (i)
When x=y=√2 then y′=3/2
Again on differentiating eq. (i) we get :
1+(y′)2+yy″+20(x2−y2−1)(2x−2yy′)(x−y′y)+5(x2−y2−1)4(1−y′2−yy″)=0
For x=y=√2 and y′=3/2 we get
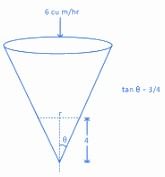
Q.4. A water tank has the shape of a right circular cone with axis vertical and vertex downwards. Its semi-vertical angle is tan-1 3/4. Water is poured in it at a constant rate of 6 cubic meter per hour. The rate (in square meter per hour), at which the wet curved surface area of the tank is increasing, when the depth of water in the tank is 4 meters, is ______________. (JEE Main 2022)
Ans. 5
Q.5. Let M and N be the number of points on the curve y5 - 9xy + 2x = 0, where the tangents to the curve are parallel to -axis and -axis, respectively. Then the value of M + N equals ___________. (JEE Main 2022)
Ans. 2
Here equation of curve is
On differentiating :
When tangents are parallel to x-axis then 9y - 2 = 0
∴ M=1.For tangent perpendicular to x-axis
5y4−9x=0 ...... (ii)
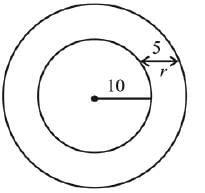
From equation (i) and (ii) we get only one point.
∴ N=1.
∴ M+N=2.
Q.6. Let the function f(x)=2x2−logex, x>0, be decreasing in (0,a) and increasing in (a,4). A tangent to the parabola y2=4ax at a point P on it passes through the point (8a, 8a−1) but does not pass through the point (−1a,0). If the equation of the normal at P is :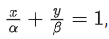 , then α+β is equal to ________________. (JEE Main 2022)
, then α+β is equal to ________________. (JEE Main 2022)
Ans. 45
so f(x) is decreasing in (0,1/2) and increasing in
It is passing through (4,3)
Butpasses through (-2,0) so rejected.
Equation of normal
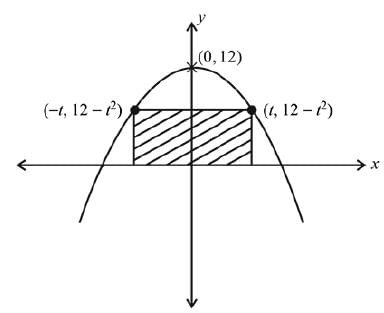
Q.7. A hostel has 100 students. On a certain day (consider it day zero) it was found that two students are infected with some virus. Assume that the rate at which the virus spreads is directly proportional to the product of the number of infected students and the number of non-infected students. If the number of infected students on 4th day is 30, then number of infected students on 8th day will be __________. (JEE Main 2022)
Ans. 90
Total students = 100
At t = 0 (zero day), infected student = 2
Let at t = t day infected student = x
At t = t day non infected student = (100 x)
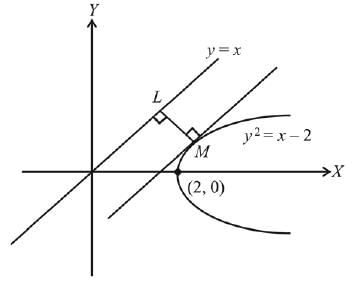
Putting value of c in equation (1), we get
Now, when t = 8, then r = ?
Q.8. Let f(x)=|(x−1)(x2−2x−3)|+x−3, x ∈ R. If m and M are respectively the number of points of local minimum and local maximum of f in the interval (0, 4), then m + M is equal to ____________. (JEE Main 2022)
Ans. 3
So, 3 points.
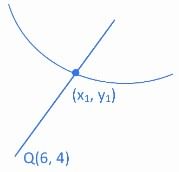
Q.9. Let l be a line which is normal to the curve y = 2x2 + x + 2 at a point P on the curve. If the point Q(6, 4) lies on the line l and O is origin, then the area of the triangle OPQ is equal to ___________. (JEE Main 2022)
Ans. 13
Q.10. Let 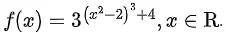 Then which of the following statements are true? (JEE Main 2022)
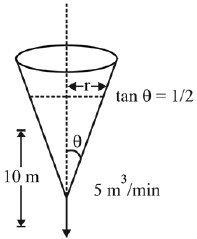
Then which of the following statements are true? (JEE Main 2022)
P : x=0 is a point of local minima of f
Q : x=√2 is a point of inflection of f
R : f′ is increasing for x>√2
(a) Only P and Q
(b) Only P and R
(c) Only Q and R
(d) All P, Q and R
Ans. d
Q.11. If the minimum value of 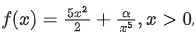 is 14 , then the value of α is equal to: (JEE Main 2022)
is 14 , then the value of α is equal to: (JEE Main 2022)
(a) 32
(b) 64
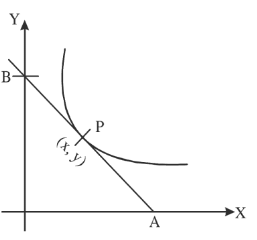
(c) 128
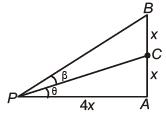
(d) 256
Ans. c
Q.12. Let 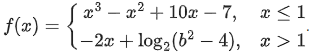
Then the set of all values of b, for which f(x) has maximum value at x = 1, is: (JEE Main 2022)
(a) (-6,-2)
(b) (2,6)
(c) 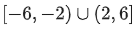
(d) 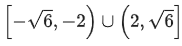
Ans. c
If f(x) has maximum value at x =1 then
Intersection of above two sets
Q.13. The curve y(x)=ax3+bx2+cx+5 touches the x-axis at the point P(−2,0) and cuts the y-axis at the point Q, where y′ is equal to 3 . Then the local maximum value of y(x) is: (JEE Main 2022)
(a) 27/4
(b) 29/4
(c) 37/4
(d) 9/2
Ans. a
Q.14. Let f(x)=4x3−11x2+8x−5, x ∈ R. Then f: (JEE Main 2022)
(a) has a local minina at x=1/2
(b) has a local minima at x=3/4
(c) is increasing in (1/2,3/4)
(d) is decreasing in (1/2,4/3)
Ans. 4
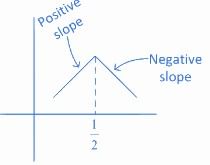
Given,f′(x) is positive before 1/2 means slope of f(x) is positive before 1/2 and f'(x) is negative after 1/2 means slope of f(x) is negative after 1/2.
∴ At 4/3,f(x) is local minimumFrom wavy curve method,
Q.15. If xy4 attains maximum value at the point (x, y) on the line passing through the points (50+, 0) and (0, 50 + α), α > 0, then (x, y) also lies on the line: (JEE Main 2022)
(a) y= 4x
(b) x = 4y
(c) y = 4x+ α
(d) x = 4y - α
Ans. a
Equation of line passing through the point (50 + α, 0) and (0, 50 +α ) is
For maximum or minimum value of p,
or
Q.16. Let λx−2y=μ be a tangent to the hyperbola a2x2−y2=b2. Then 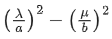 is equal to: (JEE Main 2022)
is equal to: (JEE Main 2022)
(a) -2
(b) -4
(c) 2
(d) 4
Ans. d
Q. 17. If the tangent at the point (x1, y1) on the curve y=x3+3x2+5 passes through the origin, then (x1, y1) does NOT lie on the curve : (JEE Main 2022)
(a) 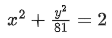
(b) 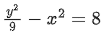
(c) 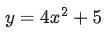
(d) 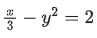
Ans. d
Given curve,
Slope of tangent,
Slope of line joined by (x1, y1) and (0, 0) is
Point (x1, y1) is on the line,x = 1 satisfy the equation
∴ (x1, y1) = (1, 9)Option D does not satisfy point (1, 9)
Q.18. The surface area of a balloon of spherical shape being inflated, increases at a constant rate. If initially, the radius of balloon is 3 units and after 5 seconds, it becomes 7 units, then its radius after 9 seconds is: (JEE Main 2022)
(a) 9
(b) 10
(c) 11
(d) 12
Ans. a
We know,
Surface area of balloon (s) = 4πr2
Given that, surface area of balloon is increasing in constant rate.
Given at t = 0, radius r = 3
∴ Equation (1) becomes
Also given, at t = 5, radius r = 7
∴ Equation (1) is
Q.19. Let λ∗ be the largest value of λ for which the function fλ(x)=4λx3−36λx2+36x+48 is increasing for all x ∈ R. Then fλ∗(1)+fλ∗(−1) is equal to: (JEE Main 2022)
(a) 36
(b) 48
(c) 64
(d) 72
Ans. d
Q.20. The slope of normal at any point (x, y), x > 0, y > 0 on the curve y = y(x) is given by
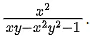 If the curve passes through the point (1, 1), then e . y(e) is equal to (JEE Main 2022)
If the curve passes through the point (1, 1), then e . y(e) is equal to (JEE Main 2022)
(a) 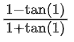
(b) tan(1)
(c) 1
(d) 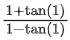
Ans. d
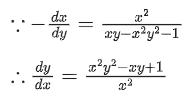
∵ y(1)=1⇒tan−1(xy)=ln x + tan−1(1)
Put x=e and y=y(e) we get
tan−1(e.y(e)) = 1+tan−11
tan−1(e.y(e))−tan−11=1
Q.21. If the angle made by the tangent at the point (x0, y0) on the curve x=12(t+sint cost), y=12(1+sint)2, 0<t < π/2, with the positive x-axis is π/3, then y0 is equal to: (JEE Main 2022)
(a) 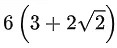
(b) 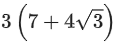
(c) 27
(d) 48
Ans. c
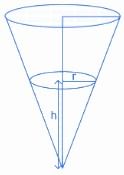
Q.22. Water is being filled at the rate of 1 cm3/ sec in a right circular conical vessel (vertex downwards) of height 35 cm and diameter 14 cm. When the height of the water level is 10 cm, the rate (in cm2/ sec) at which the wet conical surface area of the vessel increases is (JEE Main 2022)
(a) 5
(b) √21/5
(c) √26/5
(d) √26/10
Ans. c
Q.23. Consider a cuboid of sides 2x, 4x and 5x and a closed hemisphere of radius r. If the sum of their surface areas is a constant k, then the ratio x : r, for which the sum of their volumes is maximum, is: (JEE Main 2022)
(a) 2:5
(b) 19:45
(c) 3:8
(d) 19:15
Ans. b
Q.24. Let S be the set of all the natural numbers, for which the line 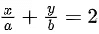 is a tangent to the curve
is a tangent to the curve 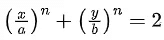 at the point (a, b), ab ≠ 0. Then: (JEE Main 2022)
at the point (a, b), ab ≠ 0. Then: (JEE Main 2022)
(a) S = ϕ
(b) n(S) = 1
(c) S = {2k : k ∈ N}
(d) S = N
Ans. d
Differentiating both sides with respect to x, we get
Equation of tangent at (a, b) is,
∴ It is tangent for all value of n.
Q.25. The sum of the absolute minimum and the absolute maximum values of the
function f(x) = |3x - x2 + 2| x in the interval [1, 2] is: (JEE Main 2022)
(a) 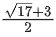
(b) 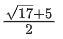
(c) 5
(d) 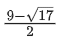
Ans. a
Q.26. Let 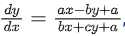 where a, b, c are constants, represent a circle passing through the point (2, 5). Then the shortest distance of the point (11, 6) from this circle is: (JEE Main 2022)
where a, b, c are constants, represent a circle passing through the point (2, 5). Then the shortest distance of the point (11, 6) from this circle is: (JEE Main 2022)
(a) 10
(b) 8
(c) 7
(d) 5
Ans. b
Above equation is circle
⇒ a = -c and b = 0
Passes through (2, 5)
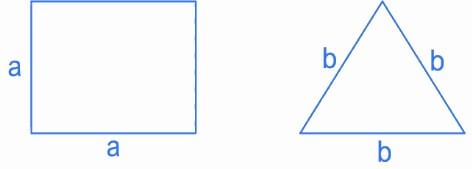
Q.27. A wire of length 22 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into an equilateral triangle. Then, the length of the side of the equilateral triangle, so that the combined area of the square and the equilateral triangle is minimum, is: (JEE Main 2022)
(a) 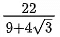
(b) 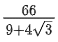
(c) 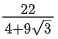
(d) 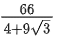
Ans. b
Q.28. The number of real roots of the equation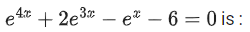 (JEE Main 2021)
(JEE Main 2021)
(a) 2
(b) 4
(c) 1
(d) 0
Ans. c
Number of real roots = 1
Q.29. A box open from top is made from a rectangular sheet of dimension a b by cutting squares each of side x from each of the four corners and folding up the flaps. If the volume of the box is maximum, then x is equal to: (JEE Main 2021)
(a) 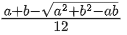
(b) 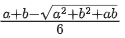
(c) 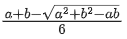
(d) 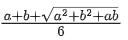
Ans. c
V = l . b . h = (a − 2x)(b − 2x) x
⇒ V(x) = (2x − a)(2x − b) x
⇒ V(x) = 4x3 − 2(a + b)x2 + abx
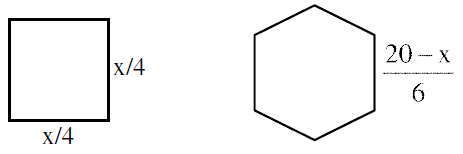
Q.30. A wire of length 20 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a regular hexagon. Then the length of the side (in meters) of the hexagon, so that the combined area of the square and the hexagon is minimum, is: (JEE Main 2021)
(a) 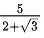
(b) 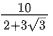
(c) 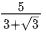
(d) 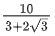
Ans. d
Let the wire is cut into two pieces of length x and 20 - x.
Length of side of regular Hexagon
Q.31. Let 'a' be a real number such that the function f(x) = ax2 + 6x − 15, x ∈ R is increasing in (−∞,3/4) and decreasing in (3/4,∞). Then the function g(x) = ax2 − 6x + 15, x ∈ R has a: (JEE Main 2021)
(a) local maximum at x = − 3/4
(b) local minimum at x = −3/4
(c) local maximum at x = 3/4
(d) local minimum at x = 3/4
Ans. a
Q.32. The maximum value of (JEE Main 2021)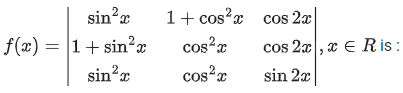
(a) √5
(b) 3/4
(c) 5
(d) √7
Ans. a
We know, maximum value of acos x ± bsin x
Q.33. Let slope of the tangent line to a curve at any point P(x, y) be given by 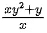 If the curve intersects the line x + 2y = 4 at x = 2, then the value of y, for which the point (3, y) lies on the curve, is : (JEE Main 2021)
If the curve intersects the line x + 2y = 4 at x = 2, then the value of y, for which the point (3, y) lies on the curve, is : (JEE Main 2021)
(a) -18/19
(b) -4/3
(c) 18/35
(d) -18/11
Ans. a
Curve intersect the line x + 2y = 4 at x = − 2
So, − 2 + 2y = 4 ⇒ y = 3
So the curve passes through (−2, 3)
It also passes through (3, y)
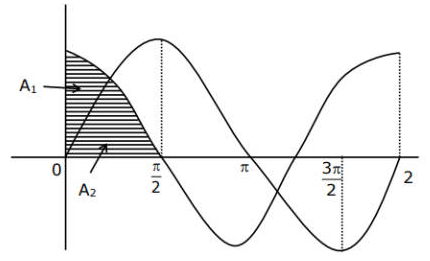
Q.34. Let A1 be the area of the region bounded by the curves y = sinx, y = cosx and y-axis in the first quadrant. Also, let A2 be the area of the region bounded by the curves y = sinx, y = cosx, x-axis and x = π/2 in the first quadrant. Then, (JEE Main 2021)
(a) 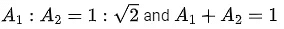
(b) 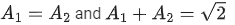
(c) 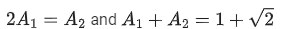
(d) 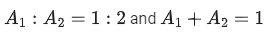
Ans. a
Q.35. The maximum slope of the curve 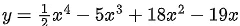 occurs at the point: (JEE Main 2021)
occurs at the point: (JEE Main 2021)
(a) (3,21/3)
(b) (0,0)
(c) (2,9)
(d) (2,2)
Ans. d
At x = 2,y = 8 - 40 + 72 - 38 = 2
∴ Required point = (2, 2)
Q.36. The minimum value of 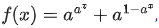 where a, x ∈ R and a > 0, is equal to: (JEE Main 2021)
where a, x ∈ R and a > 0, is equal to: (JEE Main 2021)
(a) a+ 1/a
(b) 2a
(c) a+1
(d) 2√a
Ans. d
Q.37. If the curves, 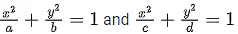 intersect each other at an angle of 90°, then which of the following relations is TRUE? (JEE Main 2021)
intersect each other at an angle of 90°, then which of the following relations is TRUE? (JEE Main 2021)
(a) a -c = b + d
(b) a + b = c + d
(c) 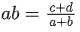
(d) a - b = c - d
Ans. d
Differentiating both sides:
Differentiating both sides :
Q.38. If the curve y = ax2 + bx + c, x ∈ R, passes through the point (1, 2) and the tangent line to this curve at origin is y = x, then the possible values of a, b, c are: (JEE Main 2021)
(a) a = − 1, b = 1, c = 1
(b) a = 1, b = 1, c = 0
(c) a = 1/2, b = 1/2, c = 1
(d) a = 1, b = 0, c = 1
Ans. b
Given curve y = ax2 + bx + c, x∈R
This curve passes through the point (1, 2)Given, slope of tangent at origin is 1
(0, 0) lie on curve
∴ c = 0, a = 1
Q.39. Let 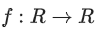 be defined as
be defined as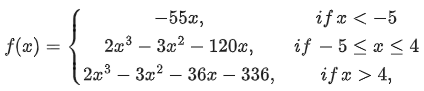
Let A = {x R : f is increasing}. Then A is equal to: (JEE Main 2021)
(a) (−5,∞)
(b) (−∞,−5)∪(4,∞)
(c) (−5,−4)∪(4,∞)
(d) (−∞,−5)∪(−4,∞)
Ans. c
Hence, f(x) is monotonically increasing in interval (−5,−4)∪(4,∞)
Q.40 For which of the following curves, the line 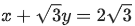 is the tangent at the point
is the tangent at the point 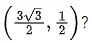 (JEE Main 2021)
(JEE Main 2021)
(a) 2x2 - 18y2 = 9
(b) 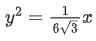
(c) x2 + 9y2 = 9
(d) x2 + y2 = 7
Ans. c
Q.41. If the tangent to the curve y = x3 at the point P(t, t3) meets the curve again at Q, then the ordinate of the point which divides PQ internally in the ratio 1 : 2 is: (JEE Main 2021)
(a) 0
(b) 2t3
(c) -2t3
(d) -t3
Ans. c
Slope of tangent at point p,
This slope is same as slope of line PQ.
Q.42. The function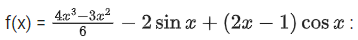 (JEE Main 2021)
(JEE Main 2021)
(a) increases in (−∞,12]
(b) decreases in (−∞,12]
(c) increases in [12,∞)
(d) decreases in [12,∞)
Ans. c
Q.43. Let f (x) be a polynomial of degree 5 such that x =±1 are its critical points. If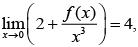 then which one of the following is not true? (2020)
then which one of the following is not true? (2020)
(a) f is an odd function.
(b) f(1) - 4f(-1) = 4.
(c) x = 1 is a point of maxima and x = −1 is a point of minimum of f.
(d) x = 1 is a point of minima and x = - 1 is a point of maxima of f.
Ans. d
Given,(1)
Let,
f(x) = 2x3 + ax4 + bx5 ⇒ f'(x) = 6x2 + 4ax3 + 5bx4
Since x = ±1 are the critical points of f (x), then
f'(1) = 6 + 4a + 5b = 0
⇒ 4a + 5b = -6... (2)
Now, f'(-1) = 0 ⇒ 6 - 4a + 5b = 0
⇒ -4a + 5b = - 6.... (3)
On solving Eqs. (2) and (3), we get
Therefore,
Hence, x = 1 is a point of maxima and x = -1 is a point of minima of f(x).
Q.44. Let f(x) = x cos-1 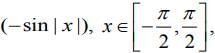 then which of the following is true? (2020)
then which of the following is true? (2020)
(a) f' is increasing in 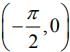 and decreasing in
and decreasing in 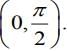
(b) f' (0) =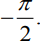
(c) f is not differentiable at x = 0.
(d) f' is decreasing in 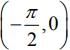 and increasing in
and increasing in 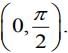
Ans. d
We have,
f(x) = x[π - cos-1
Now,
Hence, f'(x) is decreasing inand increasing in
Q.45. The length of the perpendicular from the origin, on the normal to the curve, x2 + 2xy - 3y2 at the point (2, 2) is (2020)
(a) √2
(b) 4√2
(c) 2
(d) 2√2
Ans. d
The equation of the given curve is
x2 + 2xy - 3y2 = 0
Now, the slope of normal at (2,2) is
The equation of the normal is
y −2 = −1(x−2)⇒ x+ y - 4 = 0
Hence, the length of perpendicular from origin to the normal is
Q.46. Let f(x) be a polynomial of degree 3 such that f(−1) = 10, f(1) = −6, f(x) has a critical point at x = −1 and f'(x) has a critical point x = 1. Then f(x) has a local minima at x = _________. (2020)
Ans. 3.00
Given, f'(x) has a critical point x = 1, let
Now, f '(-1) = 0
Therefore,
Now, f(1) = - 6
⇒ −11k + 6d = −36... (1)
Now, f(-1) = 10 ⇒ 5k + 6d = 60... (2)
From Eqs. (1) and (2), we get
k=5,d=6
f(x) = x3 - 3x2 - 9x + 5 ⇒ f'(x) = 3(x + 1)(x-3)
⇒ f"(x) = 6x - 6 ⇒ f"(3) = 6 x 3 - 6 = 12
Hence, f(x) has a local minima at x =3.
Q.47. A spherical iron ball of 10 cm radius is coated with a layer of ice of uniform thickness that melts at rate of 50 cm3/min. When the thickness of ice is 5 cm, then the rate (in cm/min.) at which the thickness of ice decreases, is (2020)
(a) 5/6π
(b) 1/54π
(c) 1/36π
(d) 1/18π
Ans. d
Let the initial thickness of the ice is x cm, then
At x = 5 cm and= 50 cm3/ min
We have,
Q.48. Let a function f :[0,5] →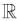 be continuous f (1) = 3 and F be defined as
be continuous f (1) = 3 and F be defined as 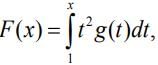 where
where 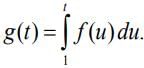 Then, for the function F, the point x = 1 is (2020)
Then, for the function F, the point x = 1 is (2020)
(a) a point of local minima.
(b) not a critical point.
(c) a point of local maxima.
(d) a point of inflection.
Ans. a
We have,.... (since f (1) = 0)
(since g (1) = 0)
⇒ F'(1) = 1.g (1) = 0.... (1)
⇒ F" (x) = 2x g (x) + x2 g' x
⇒ F" (1) = 2g (1) + 1 . g ' (1) = f(1) = 3.... (2)
From Eqs. (1) and (2), it is clear that x = 1 is the point of minima for function F.
Q.49. The maximum volume (in cu.m) of the right circular cone having slant height 3 m is: (2019)
(a) 6π
(b) 3√3π
(c) 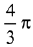
(d) 2√3π
Ans. d
...(1)
Volume of cone...(2)
For maxima/minima,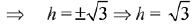
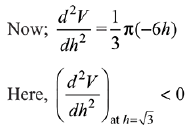
Then, h = √3 is point of maxima
Hence, the required maximum volume is,
Q.50. Let d ∈ R, and 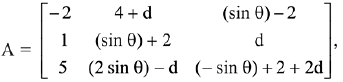 θ ∈ [0, 2π]. If the minimum value of det (A) is 8, then a value of d is: (2019)
θ ∈ [0, 2π]. If the minimum value of det (A) is 8, then a value of d is: (2019)
(a) -5
(b) -7
(c) 2(√2 + 1)
(d) 2(√2 + 2)
Ans. a
Minimum value of det (A) is attained when sin2θ = 1
⇒ d = -5 or 1
Q.51.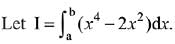 If I is minimum then the ordered pair (a, b) is: (2019)
If I is minimum then the ordered pair (a, b) is: (2019)
(a) (0,√2)
(b) (-√2,0)
(c) (√2,-√2)
(d) (-√2,√2)
Ans. d
Also,
∴ I is minimum when (a, b) = (-√2, √2)
Q.52. The tangent to the curve,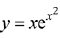 passing through the point (1, e) also passes through the point: (2019)
passing through the point (1, e) also passes through the point: (2019)
(a) (2, 3e)
(b) 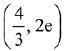
(c) 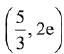
(d) (3, 6e)
Ans. b
The equation of curve
Since (1, e) lies on the curvethen equation of tangent at (1, e) is
So, equation of tangent to the curve passes through the point
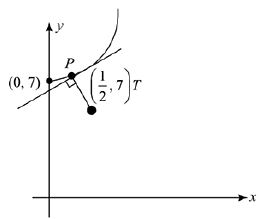
Q.53. A helicopter is flying along the curve given by y - x3/2 = 7, (x ≥ 0). A soldier positioned at the point 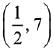 wants to shoot down the helicopter when it is nearest to him. Then this nearest distance is: (2019)
wants to shoot down the helicopter when it is nearest to him. Then this nearest distance is: (2019)
(a) 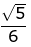
(b) 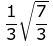
(c) 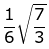
(d) 1/2
Ans. c
⇒ f(x) is increasing function ∀ x > 0
Q.54. The maximum value of the function f(x) = 3x3 -18x2 + 27x - 40 on the set S = {x ∈ R: x2 + 30 ≤ 11x } is (2019)
(a) -122
(b) -222
(c) 122
(d) 222
Ans. c
Consider the function,
f(x) = 3x(x - 3)2 - 40
Now S = {x ∈ R : x2 + 30 ≤ 11x}
So x2 - 11x + 30 < 0
⇒ x ∈ [5, 6]
∴ f(x) will have maximum value for x = 6
The maximum value of function is,
f(6) = 3 x 6 x 3 x 3 - 40 = 122.
Q.55. Let x,y be positive real numbers and m, n positive integers. The maximum value of the expression 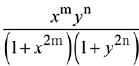 is: (2019)
is: (2019)
(a) 1
(b) 1/2
(c) 1/4
(d) None of these
Ans. c
Q.56.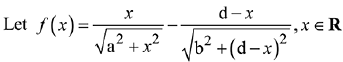 where a, b and d are non-zero real constants. Then: (2019)
where a, b and d are non-zero real constants. Then: (2019)
(a) f is an increasing function of x
(b) f is a decreasing function of x
(c) f is not a continuous function of x
(d) f is neither increasing nor decreasing function of x
Ans. a
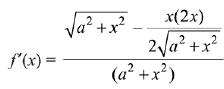
⇒ f(x) is increasing function.
Hence, f(x) is increasing function.
Q.57. The maximum area (in sq. units) of a rectangle having its base on the x-axis and its other two vertices on the parabola, y = 12 - x2 such that the rectangle lies inside the parabola, is: (2019)
(a) 36
(b) 20√2
(c) 32
(d) 18√3
Ans. c
Given, the equation of parabola is,
x2 = 12 - y
Area of the rectangle = (2t) (12 - t2)
At t = 2, area is maximum = 24(2) - 2(2)3
= 48 - 16 = 32 sq. units
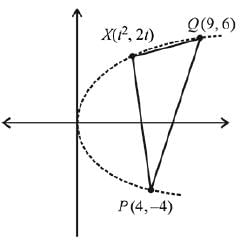
Q.58. Let P(4, -4) and Q(9, 6) be two points on the parabola, y2 = 4x and let this X be any point arc POQ of this parabola, where O is vertex of the parabola, such that the area of ΔPXQ is maximum. Then this minimum area (in sq. units) is: (2019)
(a) 75/2
(b) 125/4
(c) 625/4
(d) 125/2
Ans. b
Parametric equations of the parabola y2 = 4x are, x = t2 and y = 2t.
For maximum area t = 1/2
Q.59. The maximum value of 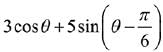 for any real value of θ is: (2019)
for any real value of θ is: (2019)
(a) 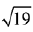
(b) 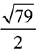
(c) 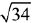
(d) 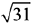
Ans. a
Let, the functions is,
Q.60. If a curve passes through the point (1, -2) and has slope of the tangent at any point (x, y) on it as 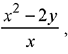 then the curve also passes through the point: (2019)
then the curve also passes through the point: (2019)
(a) (3, 0)
(b) (√3, 0)
(c) (-1, 2)
(d) (-√2, 1)
Ans. b
∵
Solution of equation
∴ curve passes through point (1, -2)
⇒ C = -9/4
Then, equation of curve
Since, above curve satisfies the point.
Hence, the curve passes through (√3, o).
Q.61. The tangent to the curves y = x2 - 5x + 5, parallel to the line 2y = 4x + 1, also passes through the point: (2019)
(a) 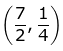
(b) 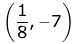
(c) 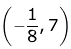
(d) 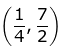
Ans. b
∵ Tangent to the given curve is parallel to line 2y = 4x + 1
∴ Slope of tangent (m) = 2
Then, the equation of tangent will be of the form
y = 2x + c ...(1)
∵ Line (1) and curve y = x2 - 5x + 5 has only one point of intersection.
∴ 2x + c = x2 - 5x + 5
x2 - 7x + (5 - c) = 0
∴ D = 49 - 4(5 - c) = 0
⇒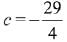
Hence, the equation of tangent:
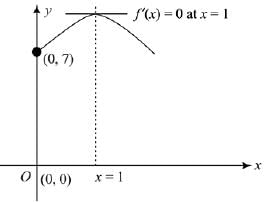
Q.62. If the function/given by f(x) = x3 - 3(a - 2)x2 + 3ax + 7, for some a ∈ R is increasing in (0, 1] and decreasing in [1, 5), then a root of the equation, 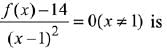 (2019)
(2019)
(a) -7
(b) 5
(c) 7
(d) 6
Ans. c
⇒
⇒
⇒ a = 5
Now,
⇒
Q.63. The shortest distance between the line y = x and the curve y2 = x - 2 is: (2019)
(a) 2
(b) 7/8
(c) 7/4√2
(d) 11/4√2
Ans. c
The shortest distance between line y = x and parabola = the distance LM between line y = x and tangent of parabola having slope 1.
Let equation of tangent of parabola having slope 1 is,
Distance between the line y - x = 0 and
Q.64. If S1 and S2 are respectively the sets of local minimum and local maximum points of the function, f(x) = 9x4 + 12x3 - 36x2 + 25, x∈R, then : (2019)
(a) S1 = {-2}; S2 = {0, 1}
(b) S1 = {-2, 0}; S2 = {1}
(c) S1 = {-2, 1}; S2 = {0}
(d) S1 = {-1}; S2 = {0,2}
Ans. c
Here at -2 & 1, f'(x) changes from negative value to positive value.
⇒ -2 & 1 are local minimum points. At 0, f'(x) changes from positive value to negative value.
⇒ 0 is the local maximum point.
Hence, S1 = {-2, 1} and S2 = {0}
Q.65. Let f : [0 : 2] → R be a twice differentiable function such that f"(x) > 0, for all x∈(0, 2). If φ(x) = (x) + f(2 - x), then φ is: (2019)
(a) increasing on (0, 1) and decreasing on (1, 2).
(b) decreasing on (0, 2)
(c) decreasing on (0, 1) and increasing on (1,2).
(d) increasing on (0, 2)
Ans. c
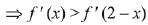
But f" (x) > 0 ⇒ f'(x) is an increasing function
Hence, φ (x) is increasing on (1, 2) and decreasing on (0, 1).
Q.66. Given that the slope of the tangent to a curve y = y(x) at any point (x, y) is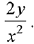 . If the curve passes through the centre of the circle x2 + y2 - 2x - 2y = 0, then its equation is : (2019)
. If the curve passes through the centre of the circle x2 + y2 - 2x - 2y = 0, then its equation is : (2019)
(a) x loge|y| = 2(x - 1)
(b) x loge |y| = - 2(x - 1)
(c) x2 |loge|y| = -2(x - 1)
(d) x loge | y | = x - 1
Ans. a
Equation (i) passes through the centre of the circle x2 + y2 - 2x - 2y = 0, i.e., (1,1)
∴ C = 2
Q.67. The height of a right circular cylinder of maximum volume inscribed in a sphere of radius 3 is: (2019)
(a) √6
(b) 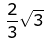
(c) 2√3
(d) √3
Ans. c
Let radius of base and height of cylinder be r and h respectively....(1)
Now, volume of cylinder, V = πr2h
Substitute the value of r2 from equation (i),
Differentiating w.r.t. h,
For maxima/minima,
⇒ Volume is maximum when h = 2√3
Q.68. If f(x) is a non-zero polynomial of degree four, having local extreme points at x = -1, 0, 1; then the set S = {x ∈ R : f(x) = f(0)} contains exactly: (2019)
(a) four irrational numbers.
(b) four rational numbers.
(c) two irrational and two rational numbers.
(d) two irrational and one rational number.
Ans. d
Since, function f(x) have local extreme points at x = -1,0, 1. Then
f(x) = K(x+ l)x(x - 1)
= K (x3 - x)
Q.69. If the tangent to the curve, y = x3 + ax - b at the point (1, -5) is perpendicular to the line, - x + y + 4 = 0, then which one of the following points lies on the curve? (2019)
(a) (-2,1)
(b) (-2,2)
(c) (2,-1)
(d) (2,-2)
Ans. d
y = x3 + ax - b
Since, the point (1, -5) lies on the curve.
⇒ 1 + a - b = - 5
⇒ a - b = -6 ...(1)
Since, required line is perpendicular to y = x - 4, then slope of tangent at the point P (1, -5) = -1
∴ 3 + a = - 1
⇒ a = -4
⇒ b = 2
the equation of the curve is y = x3 - 4x - 2
⇒ (2, -2) lies on the curve
Q.70. Let S be the set of all values of x for which the tangent to the curve y = f(x) = x3 - x2 - 2x at (x, y) is parallel to the line segment joining the points (1, f(1)) and (- 1, f(- 1)), then S is equal to: (2019)
(a) 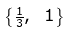
(b) 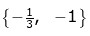
(c) 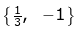
(d) 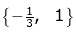
Ans. d
y = f(x) = x3 - x2 - 2x
f(1) = 1 - 1 -2 = -2, f(-1) = -1 -1+2 = 0
Since the tangent to the curve is parallel to the line segment joining the points (1, -2) and (-1, 0)
And their slopes are equal.
Hence, the required set
Q.71. A water tank has the shape of an inverted right circular cone, whose semi-vertical angle is 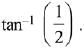 Water is poured into it at a constant rate of 5 cubic meter per minute. Then the rate (in m/min.), at which the level of water is rising at the instant when the depth of water in the tank is 10m; is: (2019)
Water is poured into it at a constant rate of 5 cubic meter per minute. Then the rate (in m/min.), at which the level of water is rising at the instant when the depth of water in the tank is 10m; is: (2019)
(a) 1/15 π
(b) 1/10 π
(c) 2/π
(d) 1/5 π
Ans. d
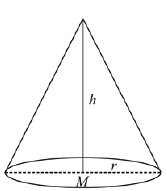
Given that water is poured into the tank at a constant rate of 5 m3/minute.
Volume of the tank is,...(i)
where r is radius and h is height at any time. By the diagram,...(ii)
Differentiate eq. (i) w.r.t. ‘t’, we get
Putting h = 10, r = 5 and dV/dt = 5 in the above equation.
Q.72. Let f(x) = ex - x and g(x) = x2 - x, ∀ x ∈ R. Then the set of all x ∈ R, where the function h(x) = (fog) (x) is increasing, is: (2019)
(a) 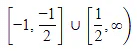
(b) 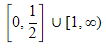
(c) 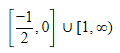
(d) 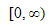
Ans. b
Given functions are, f(x) = ex - x and g(x) = x2 - x
Given f(g (x)) is increasing function.are either both positive or negative
Q.73. If the tangent to the curve 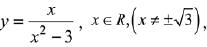 at a point (α, β) is parallel to the line 2x + 6y - 11 = 0, then : (2019)
at a point (α, β) is parallel to the line 2x + 6y - 11 = 0, then : (2019)
(a) |6α+2β|= 19
(b) |6α+2β|= 9
(c) |2α+6β|= 19
(d) |2α+6β|= 11
Ans. a
These values of α and β satisfies |6α + 2β| = 19
Q.74. A spherical iron ball of radius 10 cm is coated with a layer of ice of uniform thickness that melts at a rate of 50 cm3/min. When the thickness of the ice is 5 cm, then the rate at which the thickness (in cm/min) of the ice decreases, is: (2019)
(a) 1/18π
(b) 1/36π
(c) 5/6π
(d) 1/9π
Ans. a
Given that ice melts at a rate of 50 cm3/min
Substitute r = 5,
Q.75. Let a1, a2, a3,.... be an A. P. with a6 = 2. Then the common difference of this A.P., which maximises the product a4 a4 a5 is: (2019)
(a) 3/2
(b) 8/5
(c) 6/5
(d) 2/3
Ans. b
a6 = a + 5d = 2
Here, a is first term of A.P and d is common difference
Q.76. If m is the minimum value of k for which the function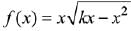 is increasing in the interval [0, 3] and M is the maximum value off in [0,3] when k = m, then the ordered pair (m, M) is equal to: (2019)
is increasing in the interval [0, 3] and M is the maximum value off in [0,3] when k = m, then the ordered pair (m, M) is equal to: (2019)
(a) (4, 3√2)
(b) (4, 3√3)
(c) (3, 3√3)
(d) (5, 3√6)
Ans. b
Given function
Differentiating w. r. t. x,
[∴ f(x) is increasing in [0, 3]]
Q.77. The equation of a common tangent to the curves, y2 = 16x and xy = - 4, is: (2019)
(a) x - y + 4 = 0
(b) x + y + 4 = 0
(c) x - 2y + 16 = 0
(d) 2x - y + 2 = 0
Ans. a
Given curves, y2 = 16x and xy = - 4
Equation of tangent to the given parabola;
∵ This is common tangent.
∴ equation of common tangent is y = x + 4
Q.78. The tangents to the curve y = (x - 2)2 -1 at its points of intersection with the line x - y = 3, intersect at the point: (2019)
(a) 
(b) 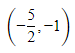
(c) 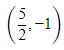
(d) 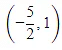
Ans. c
Tangent to the curve y = (x - 2)2 - 1 at any point (h, k) is,
Q.79. 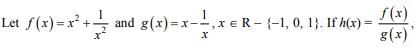 then the local minimum value of value of h(x) is: (2018)
then the local minimum value of value of h(x) is: (2018)
(a) 3
(b) -3
(c) -2√2
(d) 2√2
Ans. d
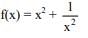
Hence, local minimum value is 2√2
Q.80. If a right circular cone, having maximum volume, is inscribed in a sphere of radius 3 cm, then the curved surface area (in cm2) of this cone is: (2018)
(a) 8√2 π
(b) 6√2 π
(c) 6√3 π
(d) 8√3 π
Ans. d
where r is radius and h is height of coin
Q.81. Let M and m be respectively the absolute maximum and the absolute minimum values of the function, f (x) = 2x3 - 9x2 + 12x + 5 in the interval [0, 3]. Then M - m is equal to: (2018)
(a) 1
(b) 9
(c) 5
(d) 4
Ans. a
For maxima or minima put f'(x) = 0
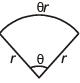
Q.82. Twenty meters of wire is available for fencing off a flower-bed in the form of a circular sector. Then the maximum area (in sq. m) of the flower-bed, is (2017)
(a) 30
(b) 12.5
(c) 10
(d) 25
Ans. d
2r + θr =20 ... (i)
A to be maximum
Hence for r = 5, A is maximum
Now, 10 + θ·5 = 20 ⇒ θ = 2 (radian)
Q.83. The function f defined by f(x) = x3 – 3x2 + 5x + 7, is: (2017)
(a) decreasing in R
(b) increasing in R
(c) increasing in (0, ∞) and decreasing in (–∞, 0)
(d) decreasing in (0, ∞) and increasing in (–∞, 0)
Ans. b
f(x) = x3 – 3x2 + 5x + 7
f'(x) = 3x2 – 6x + 5 > 0 ( ∵D< 0, a>0)
⇒x ∈ ϕ
Q.84. A tangent to the curve, y = f(x) at P(x,y) meets x-axis at A and y-axis at B. If AP : BP = 1 : 3 and f(1)= 1, then the curve also passes through the point: (2017)
(a) 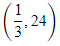
(b) 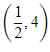
(c) 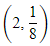
(d) 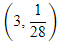
Ans. c
Let y = f(x) be a curve
slope of tangent = f'(x)
Equation of tangent (Y-y) = f'(x) (X- x)
Put Y = 0
y = 1/x3 is required curve (2, 1/8) passing through
y = 1/x3
Q.85. Let a vertical tower AB have its end A on the level ground. Let C be the mid-point of AB and P be a point on the ground such that AP = 2AB. If ∠BPC = β then tan β is (2016)
(a) 4/9
(b) 6/7
(c) 1/4
(d) 2/9
Ans. d
Q.86. If m and M are the minimum and the maximum values of 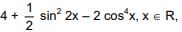 then M - m is equal to (2016)
then M - m is equal to (2016)
(a) 7/4
(b) 15/4
(c) 9/4
(d) 1/4
Ans. c
M = maximum value = 17/4
m = minimum value = 2
M-m = 17/4 - 2 = 9/4.
Q.87. Let f(x) = sin4x + cos4x. Then f is an increasing function in the interval (2016)
(a)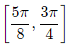
(b)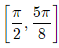
(c)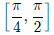
(d) 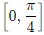
Ans. c
f(x) = sin4x + cos4x
f'(x) = 4sin3x cosx - 4cos3xsinx
= 4sinx cosx(sin2x - cos2x)
= - 2sin2x. cos2x
= - sin4x > 0
⇒ sin4x < 0
⇒ π < 4x < 2π