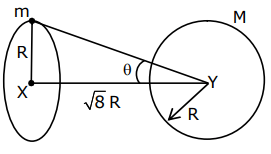
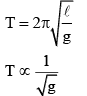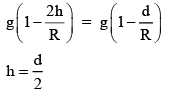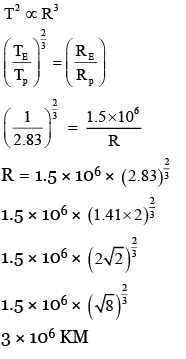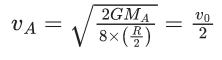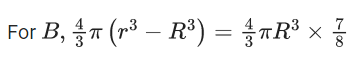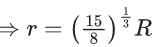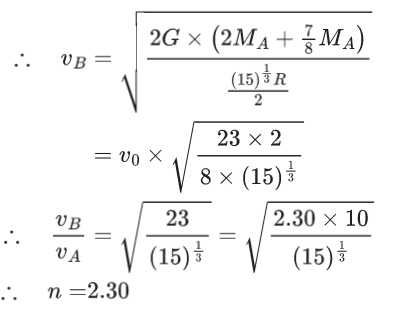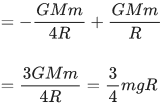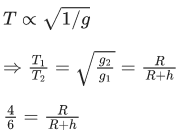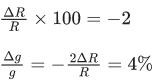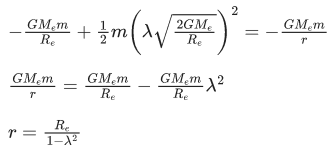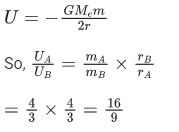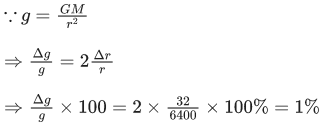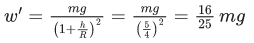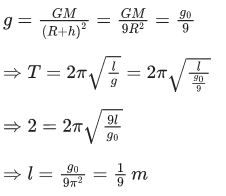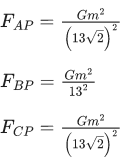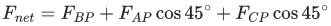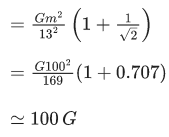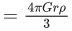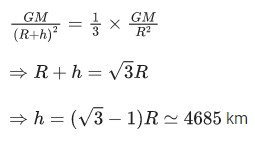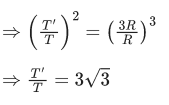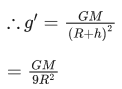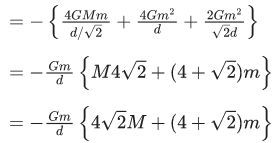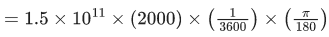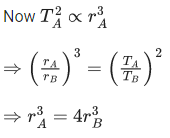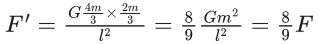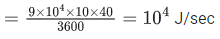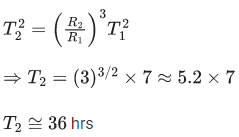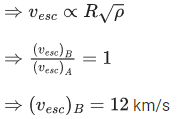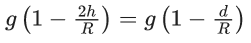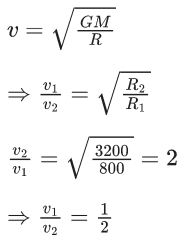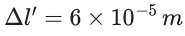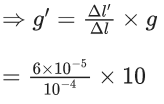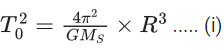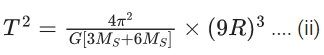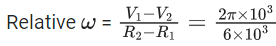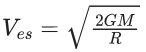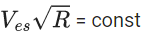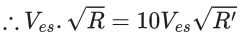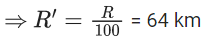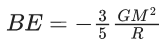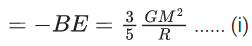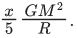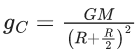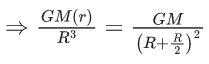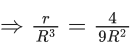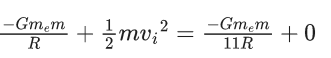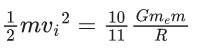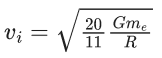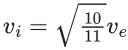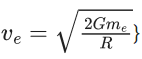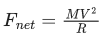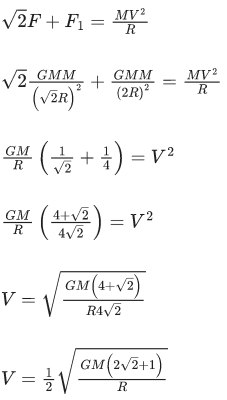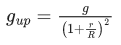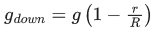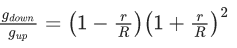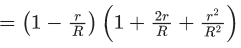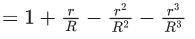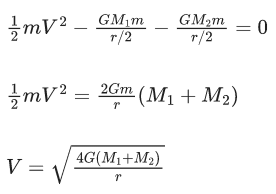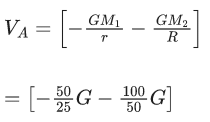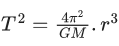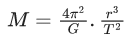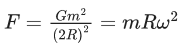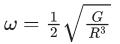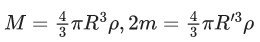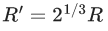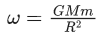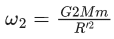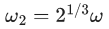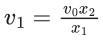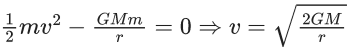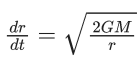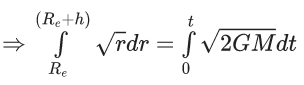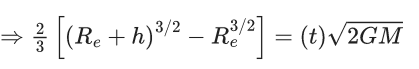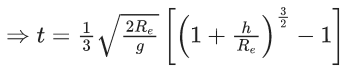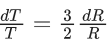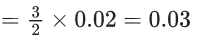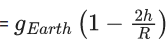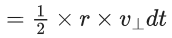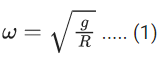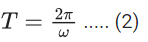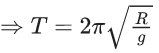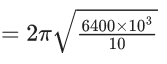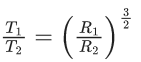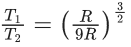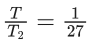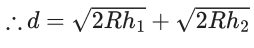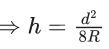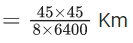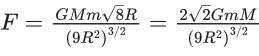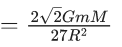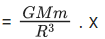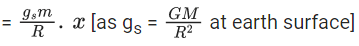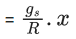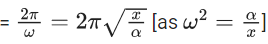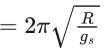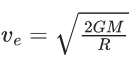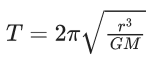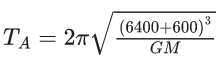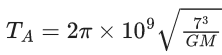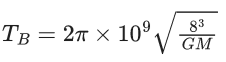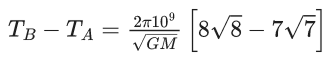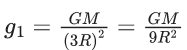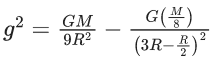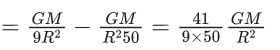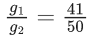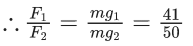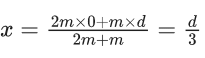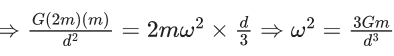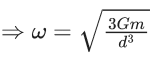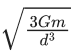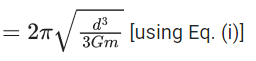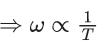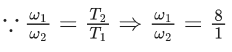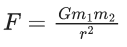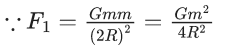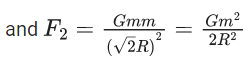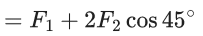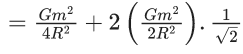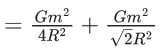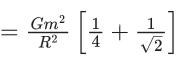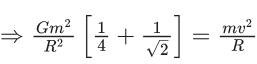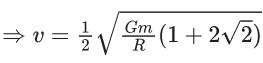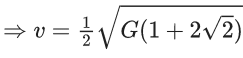Q.1. The weight of a body at the surface of earth is 18 N. The weight of the body at an altitude of 3200 km above the earth's surface is (given, radius of earth Re = 6400 km): (JEE Main 2023)
(a) 8 N
(b) 4.9 N
(c) 9.8 N
(d) 19.6 N
Ans: a
Weight on earth surface W = mg = 18 N
Q.2. Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.
Assertion A: A pendulum clock when taken to Mount Everest becomes fast.
Reason R: The value of g (acceleration due to gravity) is less at Mount Everest than its value on the surface of earth.
In the light of the above statements, choose the most appropriate answer from the options given below (JEE Main 2023)
(a) Both A and R are correct but R is NOT the correct explanation of A
(b) is correct but R is not correct
(c) Both A and R are correct and R is the correct explanation of A
(d) A is not correct but R is correct
Ans. d
on Everest g decreases, so T increases, so moves slow.
Q.3. Given below are two statements:
Statement I : Acceleration due to earth's gravity decreases as you go 'up' or 'down' from earth's surface.
Statement II : Acceleration due to earth's gravity is same at a height 'h' and depth 'd' from earth's surface, if h = d.
In the light of above statements, choose the most appropriate answer form the options given below (JEE Main 2023)
(a) Both Statement I and Statement II are incorrect
(b) Statement I is incorrect but statement II is correct
(c) Both Statement I and II are correct
(d) Statement I is correct but statement II is incorrect
Ans. d
Q.4. If the distance of the earth from Sun is 1.5 × 106 km. Then the distance of an imaginary planet from Sun, if its period of revolution is 2.83 years is : (JEE Main 2023)
(a) 6 × 106 km
(b) 3 × 106 km
(c) 3 × 107 km
(d) 6 × 107 km
Ans. b
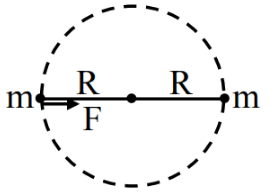
Q.5. Two spherical stars A and B have densities ρA and ρB, respectively. A and B have the same radius, and their masses MA and MB are related by MB = 2MA. Due to an interaction process, star A loses some of its mass, so that its radius is halved, while its spherical shape is retained, and its density remains ρA. The entire mass lost by A is deposited as a thick spherical shell on B with the density of the shell being ρA. If vA and vB are the escape velocities from A and B after the interaction process, the ratio 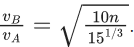 The value of n is __________. (JEE Advanced 2022)
The value of n is __________. (JEE Advanced 2022)
Ans. 2.2 and 2.4
Q.6. An object of mass 1 kg is taken to a height from the surface of earth which is equal to three times the radius of earth. The gain in potential energy of the object will be [If, g = 10 ms−2 and radius of earth = 6400 km] (JEE Main 2022)
(a) 48 MJ
(b) 24 MJ
(c) 36 MJ
(d) 12 MJ
Ans. a
ΔU = Uf − Ui
= 48 MJ
Q.7. Assume there are two identical simple pendulum clocks. Clock - 1 is placed on the earth and Clock - 2 is placed on a space station located at a height h above the earth surface. Clock - 1 and Clock - 2 operate at time periods 4 s and 6 s respectively. Then the value of h is -
(consider radius of earth RE = 6400 km and g on earth 10 m/s2) (JEE Main 2022)
(a)1200 km
(b) 1600 km
(c)( 3200 km
(d) 4800 km
Ans. c
= 3200 km
Q.8. If the radius of earth shrinks by 2% while its mass remains same. The acceleration due to gravity on the earth's surface will approximately : (JEE Main 2022)
(a) decrease by 2%
(b) decrease by 4%
(c) increase by 2%
(d) increase by 4%
Ans. d
g = GM/R2
Increase by 4%
Q.9. A body of mass m is projected with velocity λve in vertically upward direction from the surface of the earth into space. It is given that ve is escape velocity and λ < 1. If air resistance is considered to be negligible, then the maximum height from the centre of earth, to which the body can go, will be :
(R : radius of earth) (JEE Main 2022)
(a) 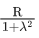
(b) 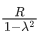
(c) 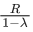
(d) 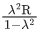
Ans. b
Using energy conservation
Q.10. Two satellites A and B, having masses in the ratio 4:3, are revolving in circular orbits of radii 3r and 4r respectively around the earth. The ratio of total mechanical energy of A to B is: (JEE Main 2022)
(a) 9 : 16
(b) 16 : 9
(c) 1 : 1
(d) 4 : 3
Ans. b
Q.11. A body is projected vertically upwards from the surface of earth with a velocity equal to one third of escape velocity. The maximum height attained by the body will be :
(Take radius of earth = 6400 km and g = 10 ms−2) (JEE Main 2022)
(a) 800 km
(b) 1600 km
(c) 2133 km
(d) 4800 km
Ans. a
Applying conservation of energy
Q.12. The percentage decrease in the weight of a rocket, when taken to a height of 32 km above the surface of earth will, be :
(Radius of earth = 6400 km) (JEE Main 2022)
(a) 1%
(b) 3%
(c) 4%
(d) 0.5%
Ans. a
⇒ % decrease in weight = 1%
Q.13. An object is taken to a height above the surface of earth at a distance 5/4 R from the centre of the earth. Where radius of earth, R = 6400 km. The percentage decrease in the weight of the object will be : (JEE Main 2022)
(a) 36%
(b) 50%
(c) 64%
(d) 25%
Ans. a
w = mg
∴ % decrease in weight
= 36%
Q.14. The length of a seconds pendulum at a height h = 2R from earth surface will be:
(Given R = Radius of earth and acceleration due to gravity at the surface of earth, g = π2 ms−2) (JEE Main 2022)
(a) 2/9 m
(b) 4/9 m
(c) 8/9 m
(d) 1/9 m
Ans. d
Q.15. Three identical particles A,B and C of mass 100 kg each are placed in a straight line with AB = BC= 13 m. The gravitational force on a fourth particle P of the same mass is F, when placed at a distance 13 m from the particle B on the perpendicular bisector of the line AC. The value of F will be approximately : (JEE Main 2022)
(a) 21 G
(b) 100 G
(c) 59 G
(d) 42 G
Ans. b
m = 100 kg
Q.16. The radii of two planets A and B are in the ratio 2 : 3. Their densities are 3ρ and 5ρ respectively. The ratio of their acceleration due to gravity is : (JEE Main 2022)
(a) 9 : 4
(b) 9 : 8
(c) 9 : 10
(d) 2 : 5
Ans. d
Given,
rA/rB = 2/3
ρA/ρB = 3/5
We know,
Acceleration due to gravity
= 2/3
Q.17. The approximate height from the surface of earth at which the weight of the body becomes 13 of its weight on the surface of earth is :
[Radius of earth R = 6400 km and √3 = 1.732] (JEE Main 2022)
(a) 3840 km
(b) 4685 km
(c) 2133 km
(d) 4267 km
Ans. b
According to the given information
Q.18. The distance between Sun and Earth is R. The duration of year if the distance between Sun and Earth becomes 3R will be : (JEE Main 2022)
(a) √3 years
(b) 3 years
(c) 9 years
(d) 3√3 years
Ans. d
We know that
T2 ∝ R3
⇒ T′ = 3√3 years
Q.19. The height of any point P above the surface of earth is equal to diameter of earth. The value of acceleration due to gravity at point P will be : (Given g = acceleration due to gravity at the surface of earth). (JEE Main 2022)
(a) g/2
(b) g/4
(c) g/3
(d) g/9
Ans. d
h = 2R
= g/9
Q.20. Given below are two statements : One is labelled as Assertion A and the other is labelled as Reason R.
Assertion A: If we move from poles to equator, the direction of acceleration due to gravity of earth always points towards the center of earth without any variation in its magnitude.
Reason R: At equator, the direction of acceleration due to the gravity is towards the center of earth.
In the light of above statements, choose the correct answer from the options given below: (JEE Main 2022)
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is NOT the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Ans. d
g′ = g0 − ω2Rcos2θ
θ = latitude.
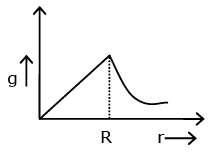
Q.21. The variation of acceleration due to gravity (g) with distance (r) from the center of the earth is correctly represented by :
(Given R = radius of earth) (JEE Main 2022)
(a) 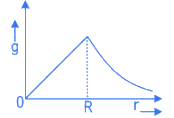
(b) 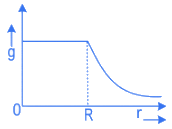
(c) 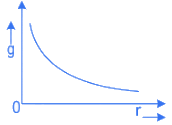
(d) 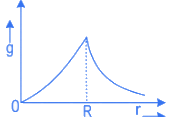
Ans. a
For r < Rg = Gmr/R3 = Cr(C= Constant)
For r > Rg = Gm/r2 = C′/r2(C′= Constant)
For the above equations the best suited graph is as given in option (A)
Q.22. Given below are two statements :
Statement I: The law of gravitation holds good for any pair of bodies in the universe.
Statement II: The weight of any person becomes zero when the person is at the centre of the earth.
In the light of the above statements, choose the correct answer from the options given below. (JEE Main 2022)
(a) Both Statement I and Statement II are true
(b) Both Statement I and Statement II are false
(c) Statement I is true but Statement II is false
(d) Statement I is false but Statement II is true
Ans. a
Statement - I is true as law of gravitation is a universal law.
Statement - II is also true as gravitational field at centre of earth is zero.
Q.23. Four spheres each of mass m from a square of side d (as shown in figure). A fifth sphere of mass M is situated at the centre of square. The total gravitational potential energy of the system is : (JEE Main 2022)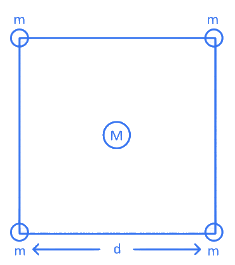 (a)
(a) 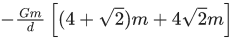
(b) 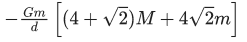
(c) 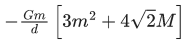
(d) 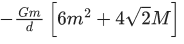
Ans. a
Total gravitational potential energy
Q.24. The distance of the Sun from earth is 1.5 × 1011 m and its angular diameter is (2000) s when observed from the earth. The diameter of the Sun will be : (JEE Main 2022)
(a) 2.45 × 1010 m
(b) 1.45 × 1010 m
(c) 1.45 × 109 m
(d) 0.14 × 109 m
Ans. c
Diameter = r × δ
= 1.45 × 109 m
Q.25. Two planets A and B of equal mass are having their period of revolutions TA and TB such that TA = 2TB. These planets are revolving in the circular orbits of radii rA and rB respectively. Which out of the following would be the correct relationship of their orbits? (JEE Main 2022)
(a) 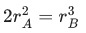
(b) 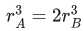
(c) 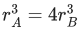
(d) 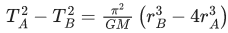
Ans. c
TA = 2TB
Q.26. Two objects of equal masses placed at certain distance from each other attracts each other with a force of F. If one-third mass of one object is transferred to the other object, then the new force will be: (JEE Main 2022)
(a) 2/9 F
(b) 16/9 F
(c) 8/9 F
(d) F
Ans. c
Let the masses are m and distance between them is l, then F =Gm2/l2.
When 1/3rd mass is transferred to the other then masses will be 4m/3 and 2m/3. so new force will be
Q.27. Water falls from a 40 m high dam at the rate of 9 × 104 kg per hour. Fifty percentage of gravitational potential energy can be converted into electrical energy. Using this hydroelectric energy number of 100 W lamps, that can be lit, is :
(Take g = 10 ms−2) (JEE Main 2022)
(a) 25
(b) 50
(c) 100
(d) 18
Ans. b
Total gravitational PE of water per second = mgh/T
50% of this energy can be converted into electrical energy so total electrical energy = 104/2 = 5000 W
So total bulbs lit can be =5000 W / 100 W = 50 bulbs
Q.28. The time period of a satellite revolving around earth in a given orbit is 7 hours. If the radius of orbit is increased to three times its previous value, then approximate new time period of the satellite will be (JEE Main 2022)
(a) 40 hours
(b) 36 hours
(c) 30 hours
(d) 25 hours
Ans. b
Q.29. The escape velocity of a body on a planet 'A' is 12 kms−1. The escape velocity of the body on another planet 'B', whose density is four times and radius is half of the planet 'A', is : (JEE Main 2022)
(a) 12 kms−1
(b) 24 kms−1
(c) 36 kms−1
(d) 6 kms−1
Ans. a
Q.30. If the acceleration due to gravity experienced by a point mass at a height h above the surface of earth is same as that of the acceleration due to gravity at a depth αh(h << Re) from the earth surface. The value of α will be _________. (JEE Main 2022)
(use Re = 6400 km)
Ans. 2
⇒ 2h = d
⇒ α = 2
Q.31. Two satellites S1 and S2 are revolving in circular orbits around a planet with radius R1 = 3200 km and R2 = 800 km respectively. The ratio of speed of satellite S1 to be speed of satellite S2 in their respective orbits would be 1/x where x = ___________. (JEE Main 2022)
Ans. 2
x = 2
Q.32. The elongation of a wire on the surface of the earth is 10−4 m. The same wire of same dimensions is elongated by 6 × 10−5 m on another planet. The acceleration due to gravity on the planet will be ____________ ms−2. (Take acceleration due to gravity on the surface of earth = 10 ms−2) (JEE Main 2022)
Ans. 6
on earth, Δl = 10−4m
on other planet
⇒ g′ = 6 m/s2
Q.33. The distance between two stars of masses 3MS and 6MS is 9R. Here R is the mean distance between the centers of the Earth and the Sun, and MS is the mass of the Sun. The two stars orbit around their common center of mass in circular orbits with period nT, where T is the period of Earth's revolution around the Sun. The value of n is __________. ( JEE Advanced 2021)
Ans. 9
For earth-sun system,
For binary system
Using Eqs. (i) and (ii), we get
T = 9T0
So, n = 9
Q.34. Two satellites revolve around a planet in coplanar circular orbits in anticlockwise direction. Their period of revolutions are 1 hour and 8 hours respectively. The radius of the orbit of nearer satellite is 2 × 103 km. The angular speed of the farther satellite as observed from the nearer satellite at the instant when both the satellites are closest is 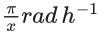 where x is ____________. (JEE Main 2021)
where x is ____________. (JEE Main 2021)
Ans. 3
T1 = 1 hour
⇒ ω1 = 2π rad/hour
T2 = 8 hours
⇒ ω2 = π/4 rad/hour
R1 = 2 × 103 km
As T2 ∝ R3
⇒ (R2/R1)3 = (T2/T1)2
⇒ R2/R1 = (8/1)2/3 = 4 ⇒ R2 = 8 × 103 kmV1 = ω1R1 = 4π × 103 km/h
V2 = ω2R2 = 2π × 103 km/h
= π/3 rad/hour
x = 3
Q.35. A body of mass (2M) splits into four masses (m, M − m, m, M − m}, which are rearranged to form a square as shown in the figure. The ratio of M/m for which, the gravitational potential energy of the system becomes maximum is x : 1. The value of x is ............ . (JEE Main 2021)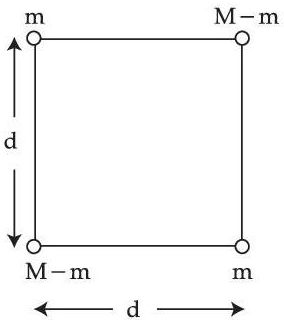
Ans. 2
Energy is maximum when mass is split equally so M/m = 2
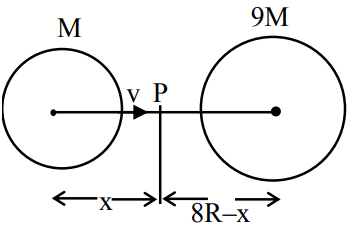
Q.36. Suppose two planets (spherical in shape) in radii R and 2R, but mass M and 9M respectively have a centre to centre separation 8 R as shown in the figure. A satellite of mass 'm' is projected from the surface of the planet of mass 'M' directly towards the centre of the second planet. The minimum speed 'v' required for the satellite to reach the surface of the second planet is 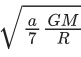 then the value of 'a' is ____________.
then the value of 'a' is ____________.
[Given : The two planets are fixed in their position] (JEE Main 2021)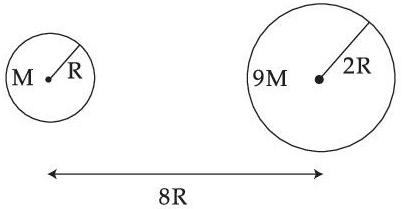
Ans. 4
Q.37. The radius in kilometer to which the present radius of earth (R = 6400 km) to be compressed so that the escape velocity is increased 10 times is ___________. (JEE Main 2021)
Ans. 64
Q.38. If one wants to remove all the mass of the earth to infinity in order to break it up completely.
The amount of energy that needs to be supplied will be 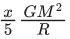 where x is __________ (Round off to the Nearest Integer) (M is the mass of earth, R is the radius of earth, G is the gravitational constant) (JEE Main 2021)
where x is __________ (Round off to the Nearest Integer) (M is the mass of earth, R is the radius of earth, G is the gravitational constant) (JEE Main 2021)
Ans. 3
We know that binding energy of earth,
∴ Energy required to break the earth into pieces
According to question, the amount of energy that needs to be supplied is
Comparing it with value in Eq. (i), we get, x = 3
Q.39. In the reported figure of earth, the value of acceleration due to gravity is same at point A and C but it is smaller than that of its value at point B (surface of the earth). The value of OA : AB will be x : y. The value of x is ________. (JEE Main 2021)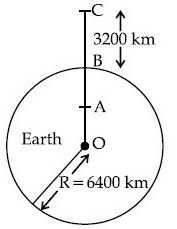
Ans. 4
Given, gA = gC
⇒ r = 4R/9
∴ OA = 4R/9
∴ AB = R − r = 5R/9
∴ OA : AB = 4 : 5
∴ x = 4
Q.40. The initial velocity vi required to project a body vertically upward from the surface of the earth to reach a height of 10R, where R is the radius of the earth, may be described in terms of escape velocity ve such that 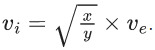 The value of x will be ____________. (JEE Main 2021)
The value of x will be ____________. (JEE Main 2021)
Ans. 10
Here R = radius of the earth
From energy conservation
{∵ escape velocity
Then the value of x = 10
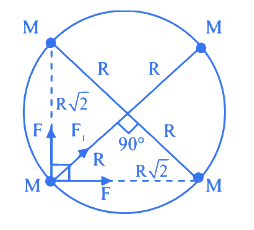
Q.41. Four particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is : (JEE Main 2021)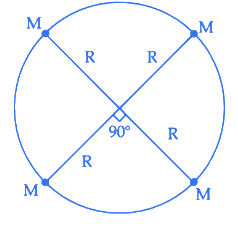 (a)
(a) 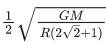
(b) 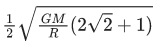
(c) 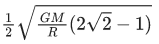
(d) 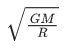
Ans. b
Let us consider the gravitational force acting on each mass M by adjacent particles be F.
and the gravitational force acting on each mass M diagonally be F1.
Along the centre of circle,
Q.42. If RE be the radius of Earth, then the ratio between the acceleration due to gravity at a depth 'r' below and a height 'r' above the earth surface is : (Given : r < RE) (JEE Main 2021)
(a) 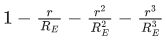
(b) 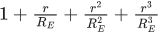
(c) 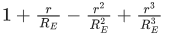
(d) 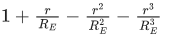
Ans. d
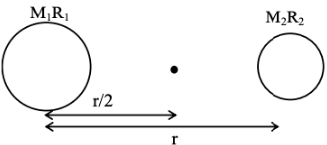
Q.43. The masses and radii of the earth and moon are (M1, R1) and (M2, R2) respectively. Their centres are at a distance 'r' apart. Find the minimum escape velocity for a particle of mass 'm' to be projected from the middle of these two masses : (JEE Main 2021)
(a) 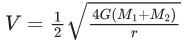
(b) 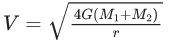
(c) 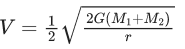
(d) 
Ans. b
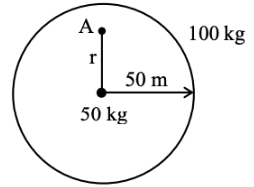
Q.44. A mass of 50 kg is placed at the centre of a uniform spherical shell of mass 100 kg and radius 50 m. If the gravitational potential at a point, 25 m from the centre is V kg/m. The value of V is : (JEE Main 2021)
(a) −60 G
(b) +2 G
(c) −20 G
(d) −4 G
Ans. d
= -4G
Q.45. Inside a uniform spherical shell :
(1) the gravitational field is zero
(2) the gravitational potential is zero
(3) the gravitational field is same everywhere
(4) the gravitational potential is same everywhere
(5) all of the above
Choose the most appropriate answer from the options given below : (JEE Main 2021)
(a) (1), (3) and (4) only
(b) (5) only
(c) (1), (2) and (3) only
(d) (2), (3) and (4) only
Ans. a
Inside a spherical shell, gravitational field is zero and hence potential remains same everywhere.
Q.46. The planet Mars has two moons, if one of them has a period 7 hours, 30 minutes and an orbital radius of 9.0 × 103 km. Find the mass of Mars. (JEE Main 2021)
(a) 5.96 × 1019 kg
(b) 3.25 × 1021 kg
(c) 7.02 × 1025 kg
(d) 6.00 × 1023 kg
Ans. d
by putting values
M = 6 x 1023
Q.47. Two identical particles of mass 1 kg each go round a circle of radius R, under the action of their mutual gravitational attraction. The angular speed of each particle is : (JEE Main 2021)
(a) 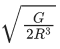
(b) 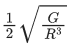
(c) 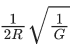
(d) 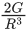
Ans. b
Q.48. Consider a planet in some solar system which has a mass double the mass of earth and density equal to the average density of earth. If the weight of an object on earth is W, the weight of the same object on that planet will be : (JEE Main 2021)
(a) 2W
(b) W
(c) 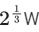
(d) √2W
Ans. c
Density is same
Q.49. The minimum and maximum distances of a planet revolving around the sun are x1 and x2. If the minimum speed of the planet on its trajectory is v0 then its maximum speed will be : (JEE Main 2021)
(a) 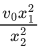
(b) 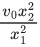
(c) 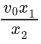
(d) 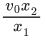
Ans. d
Angular momentum conservation equation v0x2 = v1x1
Q.50. A body is projected vertically upwards from the surface of earth with a velocity sufficient enough to carry it to infinity. The time taken by it to reach height h is ___________ s. (JEE Main 2021)
(a) 
(b) 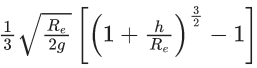
(c) 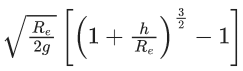
(d) 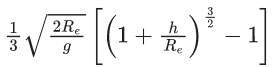
Ans. d
Q.51. A satellite is launched into a circular orbit of radius R around earth, while a second satellite is launched into a circular orbit of radius 1.02 R. The percentage difference in the time periods of the two satellites is : (JEE Main 2021)
(a) 1.5
(b) 2.0
(c) 0.7
(d) 3.0
Ans. d
T2 ∝ R3
T = kR3/2
% Change = 3%
Q.52. A person whose mass is 100 kg travels from Earth to Mars in a spaceship. Neglect all other objects in sky and take acceleration due to gravity on the surface of the Earth and Mars as 10 m/s2 and 4 m/s2 respectively. Identify from the below figures, the curve that fits best for the weight of the passenger as a function of time. (JEE Main 2021)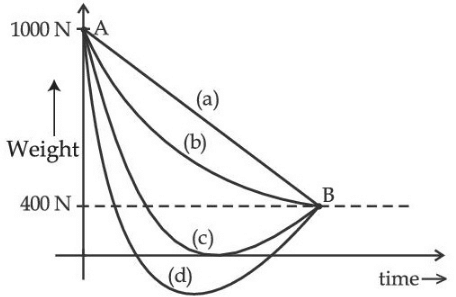 (a) (a)
(a) (a)
(b) (b)
(c) (c)
(d) (d)
Ans. b
Given,
Acceleration due to gravity on Earth, gE = 10 m/s2
and acceleration due to gravity on Mars, gM = 4 m/s2
We know that, gE (at height h)
∴ Weight at Earth, mgE = 100 × 10 = 1000 N
As the spaceship moves far away from Earth, the value of gE decreases to zero at a point where gE + gM = 0 and hence weight will also be zero.
This point is called neutral point and is shown by graph (c) in the given figure.
Then, gE increases 4ms−2 at Mars surface and weight becomes 400N which is also exhibited by graph (c).
Q.53. The angular momentum of a planet of mass M moving around the sun in an elliptical orbit is 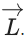 The magnitude of the areal velocity of the planet is : (JEE Main 2021)
The magnitude of the areal velocity of the planet is : (JEE Main 2021)
(a) 2L/M
(b) L/2M
(c) L/M
(c) 4L/M
Ans. b
Gravitational force line passes through the sun so torque about sun always zero for the planet
∴ Angular momentum about sum is constant.
we know, L = Mv⊥ r
Now,
Q.54. If the angular velocity of earth's spin is increased such that the bodies at the equator start floating, the duration of the day would be approximately : [Take g = 10 ms−2, the radius of earth, R = 6400 × 103 m, Take π = 3.14] (JEE Main 2021)
(a) 84 minutes
(b) 1200 minutes
(c) 60 minutes
(d) does not change
Ans. a
For objects to float
mg = 2ω2R
ω = angular velocity of earth.
R = Radius of earth
Duration of day = T
⇒ T/60 = 83.775 minutes
≃ 84 minuites
Q.55. The time period of a satellite in a circular orbit of radius R is T. The period of another satellite in a circular orbit of radius 9R is : (JEE Main 2021)
(a) 9 T
(b) 27 T
(c) 12 T
(d) 3 T
Ans. b
T2 ∝ R3
T2 = 27T
Q.56. Match List - I with List - II. (JEE Main 2021)
List - I
(A) 10 km height over earth's surface
(B) 70 km height over earth's surface
(C) 180 km height over earth's surface
(D) 270 km height over earth's surface
List - II
(i) Thermosphere
(ii) Mesosphere
(iii) Stratosphere
(iv) Troposphere
(a) (A)-(iv), (B)-(iii), (C)-(ii), (D)-(i)
(b) (A)-(i), (B)-(iv), (C)-(iii), (D)-(ii)
(c) (A)-(iii), (B)-(ii), (C)-(i), (D)-(iv)
(d) (A)-(ii), (B)-(i), (C)-(iv), (D)-(iii)
Ans. a
Troposphere:
The troposphere starts at the Earth's surface and extends 8 to 14.5 kilometers high (6 to 9 miles).
Stratosphere:
The stratosphere starts just above the troposphere and extends to 50 kilometers (31 miles) high.
Mesosphere:
The mesosphere starts just above the stratosphere and extends to 85 kilometers (53 miles) high.
Thermosphere:
The Thermosphere starts just above the mesosphere and extends to 600 kilometers (372 miles) high.
Q.57. A geostationary satellite is orbiting around an arbitrary planet 'P' at a height of 11R above the surface of 'P', R being the radius of 'P'. The time period of another satellite in hours at a height of 2R from the surface of 'P' is _________. 'P' has the time period of 24 hours. (JEE Main 2021)
(a) 3
(b) 5
(c) 6√2
(d) 6/√2
Ans. a
From Kepler's law
T2 ∝ R3
(24/T)2 = (12R/3R)3
T = 3 sec
Q.58. Two identical antennas mounted on identical towers are separated from each other by a distance of 45 km. What should nearly be the minimum height of receiving antenna to receive the signals in line of sight? (Assume radius of earth is 6400 km) (JEE Main 2021)
(a) 158.2 m
(b) 79.1 m
(c) 19.77 m
(d) 39.55 m
Ans. d
Let minimum height of receiving antenna = h2
= 0.03955 Km
= 39.55 m
Q.59. Find the gravitational force of attraction between the ring and sphere as shown in the diagram, where the plane of the ring is perpendicular to the line joining the centres. If √8R is the distance between the centres of a ring (of mass 'm') and a sphere (mass 'M') where both have equal radius 'R'. (JEE Main 2021)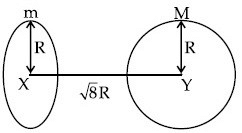 (a)
(a) 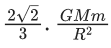
(b) 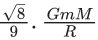
(c) 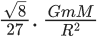
(d) 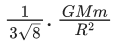
Ans. c
Q.60. A planet revolving in elliptical orbit has :
A. a constant velocity of revolution.
B. has the least velocity when it is nearest to the sun.
C. its areal velocity is directly proportional to its velocity.
D. areal velocity is inversely proportional to its velocity.
E. to follow a trajectory such that the areal velocity is constant.
Choose the correct answer from the options given below : (JEE Main 2021)
(a) D only
(b) E only
(c) C only
(d) A only
Ans. b
According to Kepler’s second law of planetary motion, areal velocity of every planet moving around the sun should remain constant in elliptical orbit.
Q.61. Assume that a tunnel is dug along a chord of the earth, at a perpendicular distance (R/2) from the earth's centre, where 'R' is the radius of the Earth. The wall of the tunnel is frictionless. If a particle is released in this tunnel, it will execute a simple harmonic motion with a time period : (JEE Main 2021)
(a) 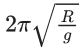
(b) g/2πR
(c) 2πR/g
(d) 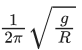
Ans. a
Value of g on the particle of mass m,
g = GMd/R3
Force acting on the particle towards the center of the earth,
F = mg
Force along the tunnel = F cosθ = F1
= mg cosθ
∴ acceleration along the tunnel
α = F1/m
Time period
Q.62. Given below are two statements : one is labelled as Assertion A and the other is labelled as Reason R.
Assertion A: The escape velocities of planet A and B are same. But A and B are of unequal mass.
Reason R: The product of their mass and radius must be same. M1R1 = M2R2
In the light of the above statements, choose the most appropriate answer from the options given below : (JEE Main 2021)
(a) Both A and R are correct and R is the correct explanation of A
(b) Both A and R are correct but R is NOT the correct explanation of A
(c) A is correct but R is not correct
(d) A is not correct but R is correct
Ans. c
ve = escape velocity
so for same ve, M1/R1 = M2/R2
A is true but R is false
Q.63. Two satellites A and B of masses 200 kg and 400 kg are revolving round the earth at height of 600 km and 1600 km respectively.
If TA and TB are the time periods of A and B respectively then the value of TB − TA :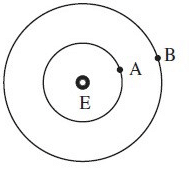 [Given : radius of earth = 6400 km, mass of earth = 6 × 1024 kg] (JEE Main 2021)
[Given : radius of earth = 6400 km, mass of earth = 6 × 1024 kg] (JEE Main 2021)
(a) 1.33 × 103 s
(b) 4.24 × 102 s
(c) 3.33 × 102 s
(d) 4.24 × 103 s
Ans. a
= 314 × 4.107
= 1289.64
= 1.289 × 103 s
Q.64. A solid sphere of radius R gravitationally attracts a particle placed at 3R from its centre with a force F1. Now a spherical cavity of radius (R/2) is made in the sphere (as shown in figure) and the force becomes F2. The value of F1 : F2 is (JEE Main 2021)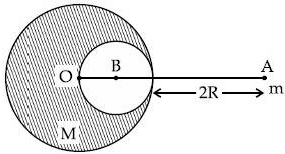 (a) 36 : 25
(a) 36 : 25
(b) 41 : 50
(c) 50 : 41
(d) 25 : 36
Ans. c
Q.65. A body weights 49N on a spring balance at the north pole. What will be its weight recorded on the same weighing machine, if it is shifted to the equator?
[Use g = GM/R2 = 9.8 ms−2 and radius of earth, R = 6400 km.] (JEE Main 2021)
(a) 49 N
(b) 49.83 N
(c) 48.83 N
(d) 49.17 N
Ans. c
Given, weight of body at North pole,
wp = mg = 49 N
Radius of Earth, R = 6400 km
Let weight of body at equator be we.
At equator, ge = g − Rω2
∴ we = mge = m(g − Rω2)
Since, wp > we ⇒ we < 49 N
Hence, above condition is satisfied by only option (b).
Q.66. Two stars of masses m and 2m at a distance d rotate about their common centre of mass in free space. The period of revolution is : (JEE Main 2021)
(a) 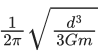
(b) 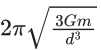
(c) 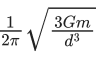
(d) 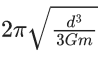
Ans. d
The given situation is shown belowThe gravitational force between these two stars provide the required centripetal force for rotation in a circle about their common centre.
Assuming 2 m at origin, the centre of mass of the system lies at
Hence, FG = FC
where, FG is gravitational force between them and FC is centripetal force.
We know that,
ω = 2π/T
∴ T = 2π/ω
Q.67. Consider two satellites S1 and S2 with periods of revolution 1 hr. and 8 hr. respectively revolving around a planet in circular orbits. The ratio of angular velocity of satellite S1 to the angular velocity of satellite S2 is : (JEE Main 2021)
(a) 1 : 4
(b) 8 : 1
(c) 2 : 1
(d) 1 : 8
Ans. b
Given, period of revolution of first satellite,
T1 = 1h
Period of revolution of second satellite,
T2 = 8h
We know that, ω = 2π/T
or ω1 : ω2 = 8 : 1
Q.68. Four identical particles of equal masses 1 kg made to move along the circumference of a circle of radius 1 m under the action of their own mutual gravitational attraction. The speed of each particle will be : (JEE Main 2021)
(a) 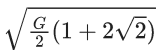
(b) 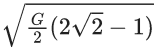
(c) 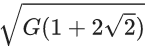
(d) 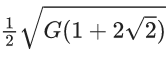
Ans. d
Given, m = 1 kg, R = 1 m
We know that,
Net force on one particle,
As the gravitational force provides the necessary centripetal force, so
Fnet = FC= mv2/R
Here, FC = centripetal force.