JEE Main Previous year questions (2021-22): Matrices and Determinants - 2 - Notes | Study Maths 35 Years JEE Main & Advanced Past year Papers - JEE

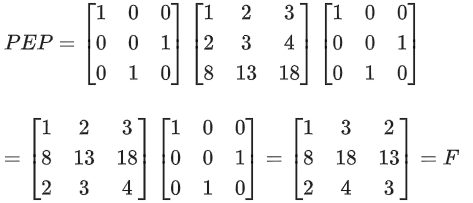
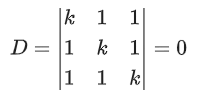
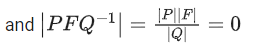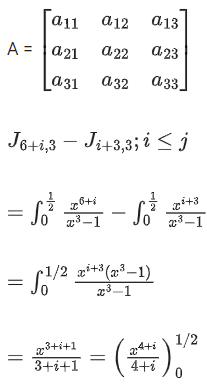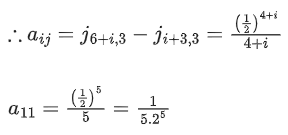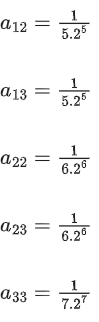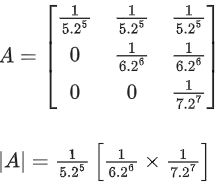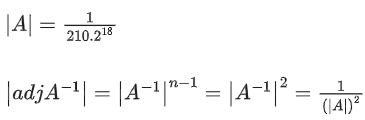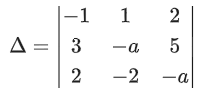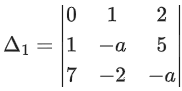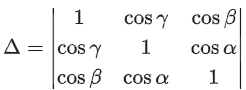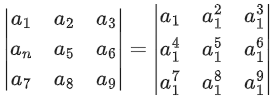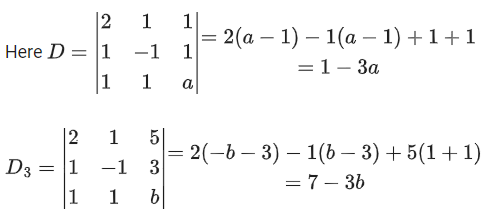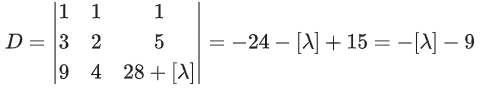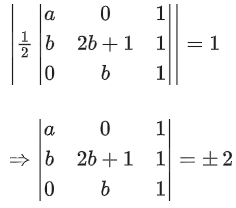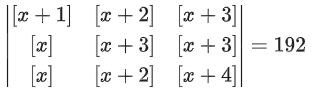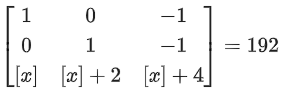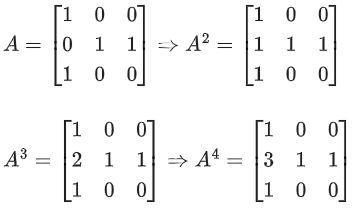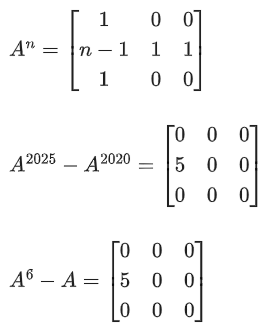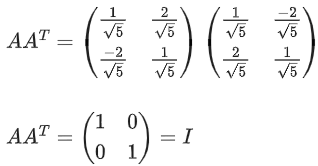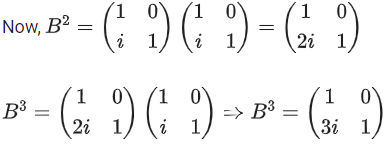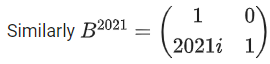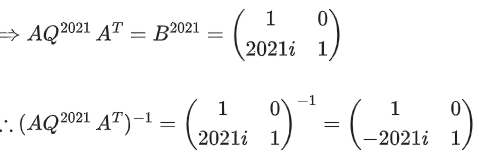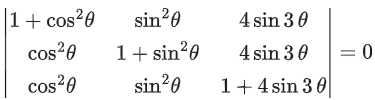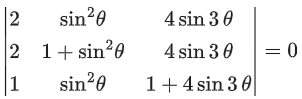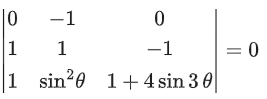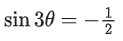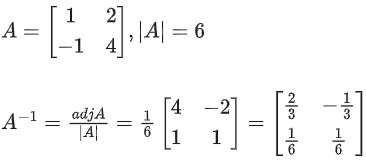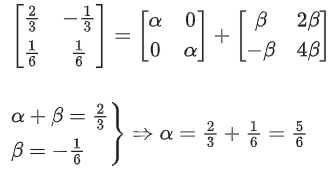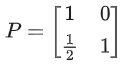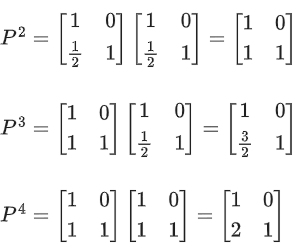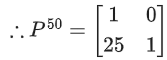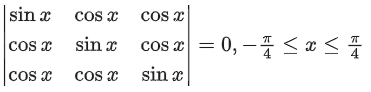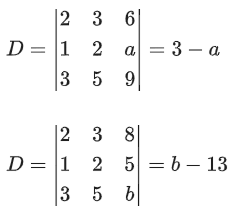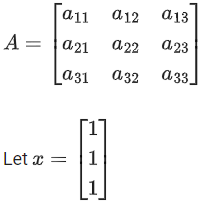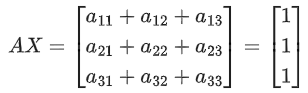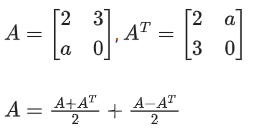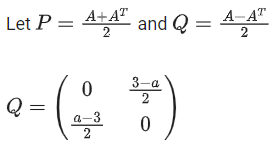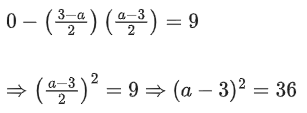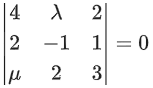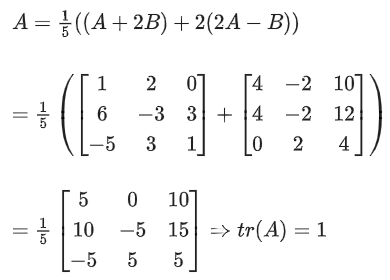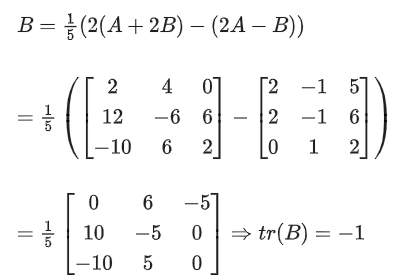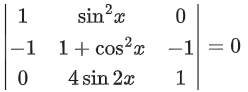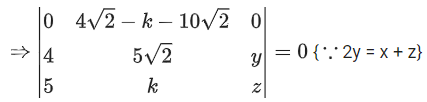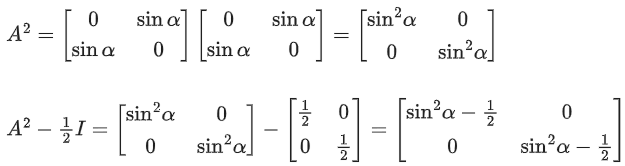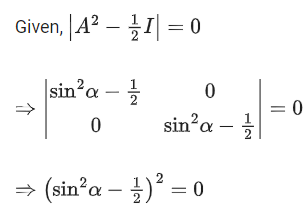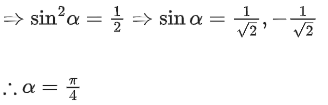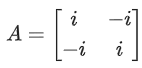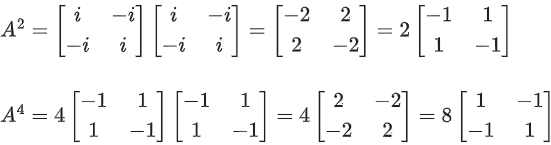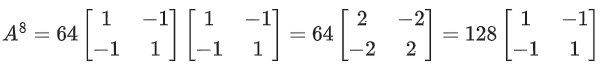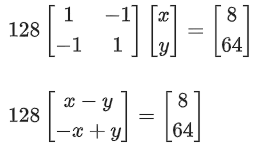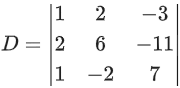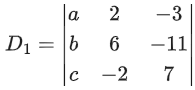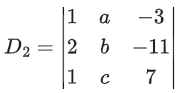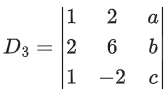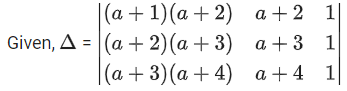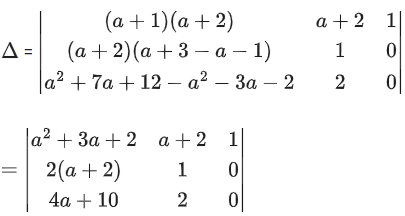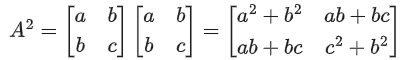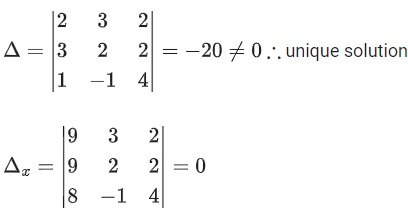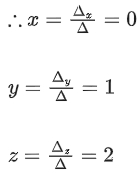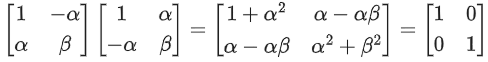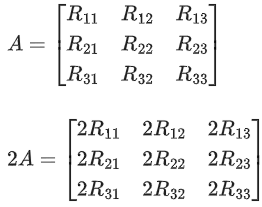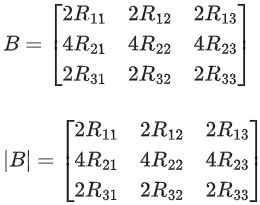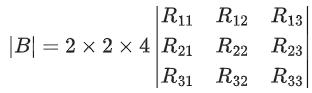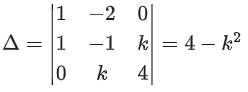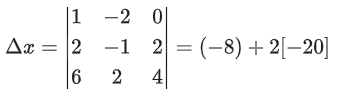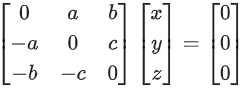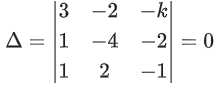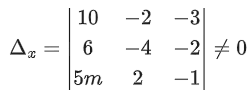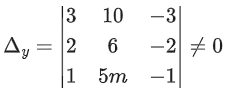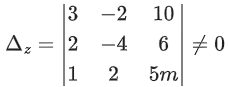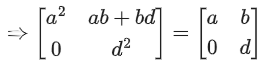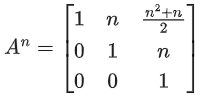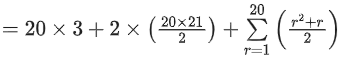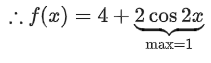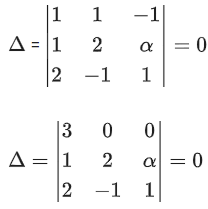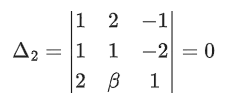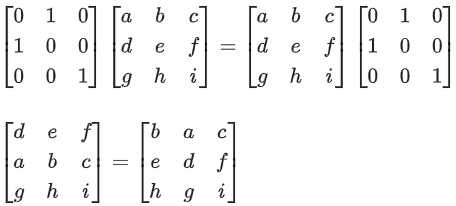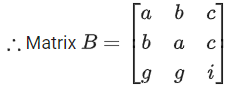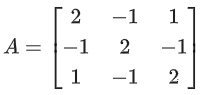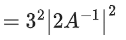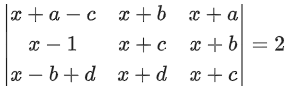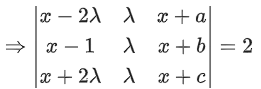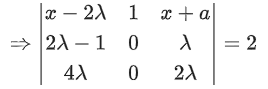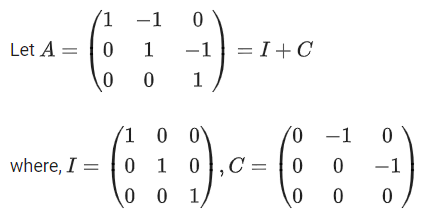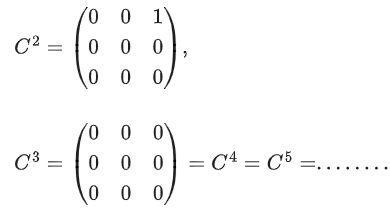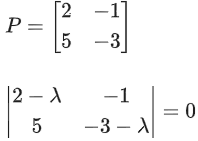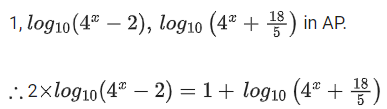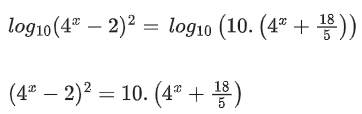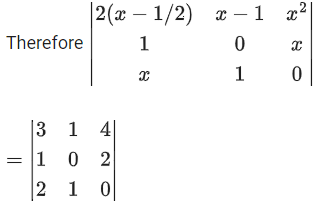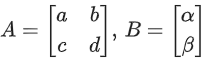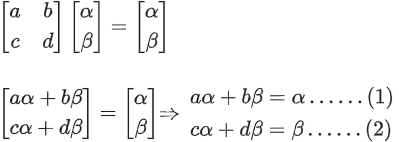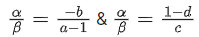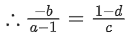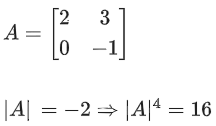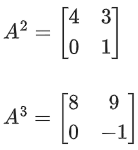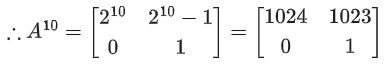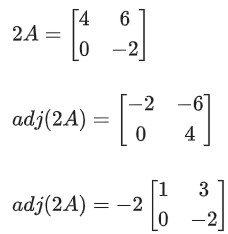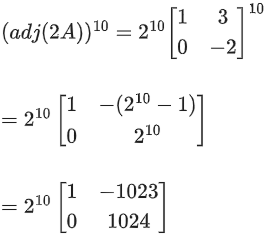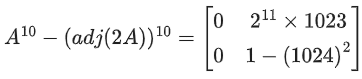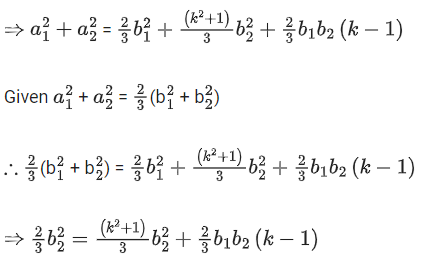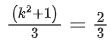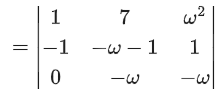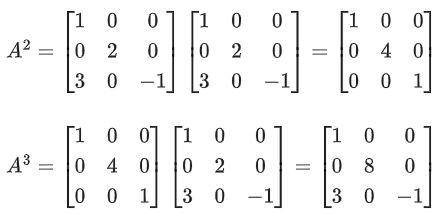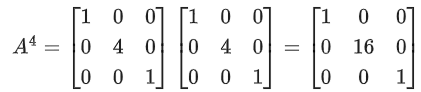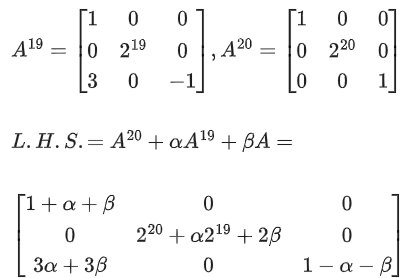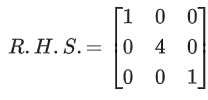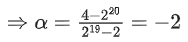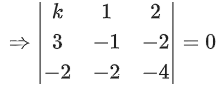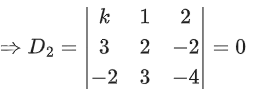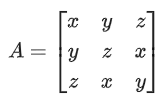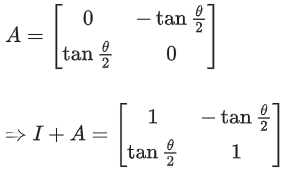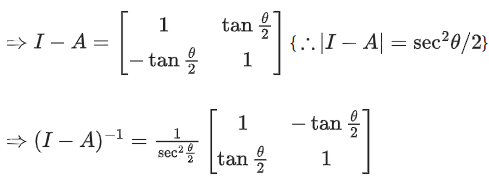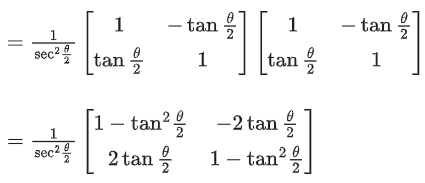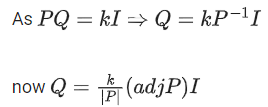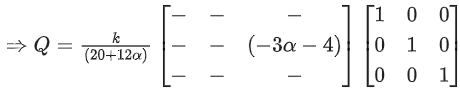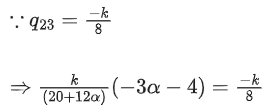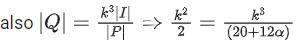Q.53. For any 3 × 3 matrix M, let |M| denote the determinant of M. Let I be the 3 × 3 identity matrix. Let E and F be two 3 × 3 matrices such that (I − EF) is invertible. If G = (I − EF)⁻¹, then which of the following statements is (are) TRUE?       (JEE Advanced 2021)
(a) | FE | = | I − FE| | FGE |
(b) (I − FE)(I + FGE) = I
(c) EFG = GEF
(d) (I − FE)(I − FGE) = I

Ans. a, b, c
∵ I − EF = G⁻¹ ⇒ G − GEF = I ..... (i)
and G − EFG = I ..... (ii)
Clearly, GEF = EFG → option (c) is correct.
Also, (I − FE) (I + FGE)
= I − FE + FGE − FEFGE
= I − FE + FGE − F(G − I) E
= I − FE + FGE − FGE + FE
= I → option (b) is correct but option (d) is incorrect.
∵ (I − FE) (I − FGE) = I − FE − FGE + F(G − I) E
= I − 2FE
Now, (I − FE) (− FGE) = − FE
⇒ | I − FE | | FGE | = | FE |
→ option (a) is correct.

Q.54. For any 3 × 3 matrix M, let | M | denote the determinant of M. Let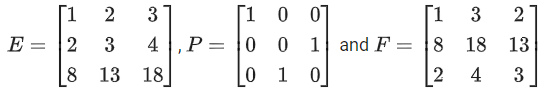

If Q is a nonsingular matrix of order 3 × 3, then which of the following statements is(are) TRUE?       (JEE Advanced 2021)
(a) F = PEP and P2 =
(b) | EQ + PFQ⁻¹ | = | EQ | + | PFQ⁻¹ |
(c) | (EF)³ | > | EF |²
(d) Sum of the diagonal entries of P⁻¹EP + F is equal to the sum of diagonal entries of E + P⁻¹FP 

Ans. a, b, d
For option (a)


Hence, option (a) is correct.
For option (b)
|EQ + PFQ⁻¹| = |EQ| + |PFQ⁻¹| .... (i)
∵ | E | = 0 and | F | = 0 and | Q | ≠ 0
∴ |EQ| = |E||Q| = 0

Let R = EQ + PFQ⁻¹ .... (ii)
⇒ RQ = EQ² + PF = EQ² + P²EP = EQ² + EP [∵ P² = I]
= E(Q² + P)
⇒ |RQ| = |E(Q² + P)|
⇒ |R||Q| = |E||Q² + P| = 0 [∵ | E | = O]
⇒ |R| = 0 (as |Q| ≠ 0) ..... (iii)
From Eqs. (ii) and (iii), we get Eq. (i) is true.
Hence, option (b) is correct.
For option (c)
|(EF)³| > |EF|²
i.e. 0 > 0 which is false.
For option (d)
∵ P² = I ⇒ P⁻¹ = P
∴ P⁻¹FP = PFP = PPEPP = E
So, E + P⁻¹FP = E + E = 2E
⇒ Tr(E + P⁻¹FP) = Tr(2E) = 2Tr(E) ..... (iv)
and P⁻¹EP + F
⇒ PEP + F = 2PEP [∵ F = PEP]
∴ Tr(2PEP)=2Tr(PEP)=2Tr(F)=2Tr(E) ..... (v)
From Eqs. (iv) and (v) option (d) is also correct.

Q.55. Let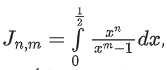∀ n > m and n, m ∈ N. Consider a matrix A = [a_ij]_{3 × 3} where 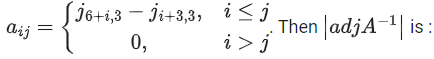      (JEE Main 2021)
(a) (15)² × 2⁴² 
(b) (15)² × 2³⁴ 
(c) (105)² × 2³⁸ 
(d) (105)² × 2³⁶

Ans. c





= (210.2¹⁸)²
= (105)² × 2³⁸

Q.56. Consider the system of linear equations
−x + y + 2z = 0
3x − ay + 5z = 1
2x − 2y − az = 7
Let S₁ be the set of all a ∈ R for which the system is inconsistent and S₂ be the set of all a∈R for which the system has infinitely many solutions. If n(S₁) and n(S₂) denote the number of elements in S₁ and S₂ respectively, then       (JEE Main 2021)
(a) n(S₁) = 2, n(S₂) = 2
(b) n(S₁) = 1, n(S₂) = 0
(c) n(S₁) = 2, n(S₂) = 0
(d) n(S₁) = 0, n(S₂) = 2

Ans. c

= −1(a² + 10) − 1(−3a − 10) + 2(−6 + 2a)
= −a² − 10 + 3a + 10 − 12 + 4a
Δ = −a² + 7a − 12
Δ = −[a² − 7a + 12]
Δ = −[(a − 3)(a − 4)]

= a + 35 − 4 + 14a
= 15a + 31
Now, Δ₁ = 15a + 31
For inconsistent Δ = 0 ∴ a = 3, a = 4 and for a = 3 and 4, Δ₁ ≠ 0
n(S₁) = 2
For infinite solution: Δ = 0 and Δ₁ = Δ₂ = Δ₃ = 0
Not possible
∴ n(S₂) = 0

Q.57. If α + β + γ = 2π, then the system of equations
x + (cos γ)y + (cos β)z = 0
(cos γ)x + y + (cos α)z = 0
(cos β)x + (cos α)y + z = 0 has:       (JEE Main 2021)
(a) no solution
(b) infinitely many solution
(c) exactly two solutions
(d) a unique solution

Ans. b
Given α + β + γ = 2π

= 1 − cos²α − cos⁡γ(cos⁡γ − cos⁡α cos⁡β) + cos⁡β(cos⁡α cos⁡γ − cos⁡β)

= 1 − cos²α − cos²β − cos²γ + 2cos⁡α cos⁡β cos⁡γ

= sin²α − cos²β − cos⁡γ(cos⁡γ − 2cos⁡α cos⁡β)

= −cos⁡(α + β)cos⁡(α − β) − cos⁡γ(cos⁡(2π − (α − β)) − 2cos⁡α cos⁡β)

= −cos⁡(2π − γ)cos⁡(α − β) − cos⁡γ(cos⁡(α + β) − 2cos⁡α cos⁡β)

= −cos⁡γ cos⁡(α − β) + cos⁡γ(cos⁡α cos⁡β + sin⁡α sin⁡β)

= −cos⁡γ cos⁡(α − β) + cos⁡γ cos⁡(α − β)

= 0

So, the system of equation has infinitely many solutions.

Q.58. If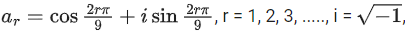then the determinant is equal to:       (JEE Main 2021)
(a) a₂a₆ − a₄a₈ 
(b) a₉ 
(c) a₁a₉ − a₃a₇ 
(d) a₅

Ans. c
r = 1, 2, 3, ......, a₁, a₂, a₃, ..... are in G.P.


Now, a₁a₉ − a₃a₇ = a₁¹⁰ − a₁¹⁰ = 0

Q.59. If the following system of linear equations
2x + y + z = 5
x − y + z = 3
x + y + az = b
has no solution, then:       (JEE Main 2021)
(a)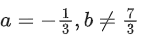
(b)
(c)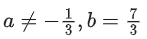
(d)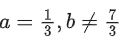

Ans. d

forsystem has no solutions.

Q.60. Let [λ] be the greatest integer less than or equal to λ. The set of all values of λ for which the system of linear equations
x + y + z = 4,
3x + 2y + 5z = 3,
9x + 4y + (28 + [λ])z = [λ] has a solution is:       (JEE Main 2021)
(a) R
(b) (−∞, −9) ∪ (−9, ∞)
(c) [−9, −8)
(d) (−∞, −9) ∪ [−8, ∞)

Ans. a

if [λ] + 9 ≠ 0 then unique solution
if [λ] + 9 = 0 then D₁ = D₂ = D₃ = 0
so infinite solutions
Hence, λ can be any red number. 

Q.61. Let A(a, 0), B(b, 2b + 1) and C(0, b), b ≠ 0, |b| ≠ 1, be points such that the area of triangle ABC is 1 sq. unit, then the sum of all possible values of a is:       (JEE Main 2021)
(a)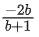
(b)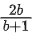
(c)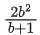
(d)

Ans. d

⇒ a(2b + 1 − b) − 0 + 1(b² − 0) = ±2


Sum of possible values of 'a' is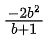
 

Q.62. Let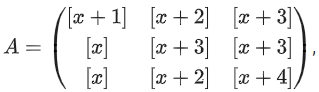where [t] denotes the greatest integer less than or equal to t. If det(A) = 192, then the set of values of x is the interval:       (JEE Main 2021)
(a) [68, 69)
(b) [62, 63)
(c) [65, 66)
(d) [60, 61)

Ans. b

R₁ → R₁ − R₃ & R₂ → R₂ − R₃ 

2[x] + 6 + [x] = 192 ⇒ [x] = 62

Q.63. If the matrix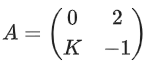satisfies A(A³ + 3I) = 2I, then the value of K is:       (JEE Main 2021)
(a) 1/2
(b)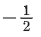
(c) -1
(d) 1

Ans. a

A⁴ + 3IA = 2I
⇒ A⁴ = 2I − 3A
Also characteristic equation of A is |A−λI|=0

⇒ λ + λ² − 2k = 0
⇒ A + A² = 2K . I
⇒ A² = 2KI − A
⇒ A⁴ = 4K²I + A² − 4AK
Put A² = 2KI − A
and A⁴ = 2I − 3A
2I − 3A = 4K²I + 2KI − A − 4AK
⇒ I(2 − 2K − 4K²) = A(2 − 4K)
⇒ −2I(2K² + K − 1) = 2A(1 − 2K)
⇒ −2I(2K − 1)(K + 1) = 2A(1 − 2K)
⇒ (2K − 1)(2A) − 2I(2K − 1)(K + 1) = 0
⇒ (2K − 1)[2A − 2I(K + 1)] = 0
⇒ K = 1/2

Q.64. Let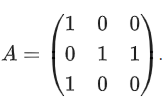Then A²⁰²⁵ − A²⁰²⁰ is equal to:       (JEE Main 2021)
(a) A⁶ − A 
(b) A⁵ 
(c) A⁵ − A 
(d) A⁶

Ans. a

Q.65. If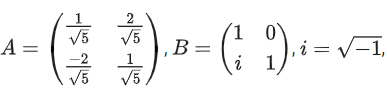and Q = A^TBA, then the inverse of the matrix A Q²⁰²¹ A^T is equal to:        (JEE Main 2021)
(a)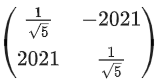
(b)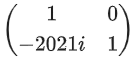
(c)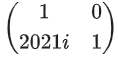
(d)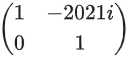

Ans. b

Q² = A^TBAA^TBA = A^TBIBA
⇒ Q² = A^TB2A
Q³ = A^TB²AA^TBA ⇒ Q³ = A^TB³A
Similarly: Q²⁰²¹ = A^TB²⁰²¹A


∴ AQ²⁰²¹ = A^T = AA^TB²⁰²¹AA^T = IB²⁰²¹I

Q.66. Let θ ∈ (0, π/2). If the system of linear equations
(1 + cos²θ)x + sin²θy + 4sin⁡3θz = 0
cos²θx + (1 + sin²θ)y + 4sin⁡3θz = 0
cos²θx + sin²θy + (1 + 4sin⁡3θ)z = 0
has a non-trivial solution, then the value of θ is:        (JEE Main 2021)
(a) 4π/9
(b) 7π/18
(c) π/18
(d) 5π/18

Ans. b

C₁ → C₁ + C₂

R₁ → R₁ − R₂, R₂ → R₂ − R₃

or 4sin⁡3θ = −2

θ = 7π/18

Q.67. Let A and B be two 3 × 3 real matrices such that (A² − B²) is invertible matrix. If A⁵ = B⁵ and A³B² = A²B³, then the value of the determinant of the matrix A³ + B³ is equal to:        (JEE Main 2021) 
(a) 2
(b) 4
(c) 1
(d) 0

Ans. d
C = A² − B²; | C | ≠ 0
A² = B⁵ and A³B² = A²B²
Now, A⁵ − A³B² = B⁵ − A²B³
⇒ A³ (A² − B²) + B³ (A² − B²) = 0
⇒ (A³ + B³(A² − B²) = 0
⇒ A³ + B³ = 0 (∵|A² − B² ≠ 0|)

Q.68. Let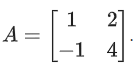 If A⁻¹ = αI + βA, α, β ∈ R, I is a 2 × 2 identity matrix then 4(α − β) is equal to:         (JEE Main 2021) 
(a) 5
(b) 8/3
(c) 2
(d) 4

Ans. d


∴ 4(α − β) = 4(1) = 4

Q.69. If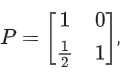 then P⁵⁰ is:          (JEE Main 2021) 
(a)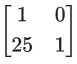
(b)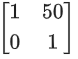
(c)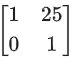
(d)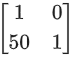

Ans. a

Q.70. The number of distinct real roots of 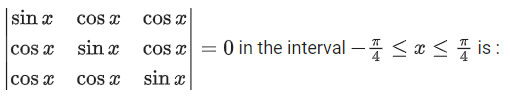         (JEE Main 2021)
(a) 4 
(b) 1 
(c) 2 
(d) 3 

Ans. b

Apply: R₁ → R₁ − R₂ & R₂ → R₂ − R₃ 

⇒ (sin⁡x − cos⁡x)²(sin⁡x + 2cos⁡x) = 0 
∴ x = π/4

Q.71. The values of a and b, for which the system of equations
2x + 3y + 6z = 8
x + 2y + az = 5
3x + 5y + 9z = b
has no solution, are:        (JEE Main 2021)
(a) a = 3, b ≠ 3 
(b) a ≠ 3, b ≠ 13 
(c) a ≠ 3, b = 3
(d) a = 3, b = 13

Ans. a

If a = 3, b ≠ 13, no solution.

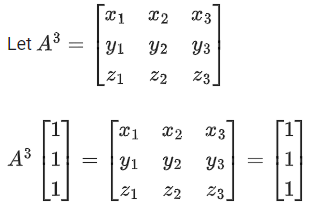
Q.72. Let A = [a_ij] be a real matrix of order 3 × 3, such that a_i1 + a_i2 + a_i3 = 1, for i = 1, 2, 3. Then, the sum of all the entries of the matrix A³ is equal to:        (JEE Main 2021)
(a) 2
(b) 1
(c) 3
(d) 9

Ans. c


⇒ AX = X
Replace X by AX
A²X = AX = X
Replace X by AX
A³X = AX = X

Sum of all the element = 3

Q.73. The values of λ and μ such that the system of equations x + y + z = 6, 3x + 5y + 5z = 26, x + 2y + λz = μ has no solution, are:        (JEE Main 2021)
(a) λ = 3, μ = 5
(b) λ = 3, μ ≠ 10
(c) λ ≠ 2, μ = 10
(d) λ = 2, μ ≠ 10 

Ans. d
x + y + z = 6 ..... (i)
3x + 5y + 5z = 26 .... (ii)
x + 2y + λz = μ ..... (iii)
5 × (i) − (ii) ⇒ 2x = 4 ⇒ x = 2
∴ from (i) and (iii)
y + z = 4 ..... (iv)
2y + λz = μ − 2 .....(v)
(v) − 2 × (iv)
⇒ (λ − 2)z = μ − 10

∴ For no solution λ = 2 and μ ≠ 10.

Q.74. The value of k ∈ R, for which the following system of linear equations
3x − y + 4z = 3,
x + 2y − 3z = −2
6x + 5y + kz = −3,
has infinitely many solutions, is:        (JEE Main 2021)
(a) 3
(b) −5
(c) 5
(d) −3

Ans. b

⇒ 3(2k + 15) + K + 18 − 28 = 0
⇒ 7k + 35 = 0
⇒ k = − 5 

Q.75. Let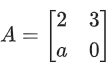, a ∈ R be written as P + Q where P is a symmetric matrix and Q is skew symmetric matrix. If det(Q) = 9, then the modulus of the sum of all possible values of determinant of P is equal to:        (JEE Main 2021)
(a) 36
(b) 24
(c) 45
(d) 18

Ans. a


Det (Q) = 9 

a − 3 = ±6 ⇒ a = 9, −3

| P | = - 36 or 0
∴ | −36 + 0 | = 36

Q.76. Define a relation R over a class of n × n real matrices A and B as
"ARB iff there exists a non-singular matrix P such that PAP⁻¹ = B".
Then which of the following is true?        (JEE Main 2021)
(a) R is reflexive, transitive but not symmetric
(b) R is symmetric, transitive but not reflexive
(c) R is reflexive, symmetric but not transitive
(d) R is an equivalence relation

Ans. d
For reflexive relation,
∀(A, A) ∈ R for matrix P.
⇒ A = PAP⁻¹ is true for P = 1
So, R is reflexive relation.
For symmetric relation,
Let (A, B) ∈ R for matrix P.
⇒ A = PBP⁻¹
After pre-multiply by P⁻¹ and post-multiply by P, we get
P⁻¹AP = B
So, (B, A) ∈ R for matrix P⁻¹.
So, R is a symmetric relation.
For transitive relation,
Let ARB and BRC
So, A = PBP⁻¹ and B = PCP⁻¹
Now, A = P(PCP⁻¹)P⁻¹
⇒ A = (P)²C(P⁻¹)² ⇒ A = (P)² ⋅ C ⋅ (P²)⁻¹
∴(A, C) ∈ R for matrix P².
∴ R is transitive relation.
Hence, R is an equivalence relation. 

Q.77. Let the system of linear equations
4x + λy + 2z = 0
2x − y + z = 0
μx + 2y + 3z = 0, λ, μ ∈ R.
has a non-trivial solution. Then which of the following is true?        (JEE Main 2021)
(a) μ = 6, λ ∈ R
(b) λ = 3, μ ∈ R
(c) μ = −6, λ ∈ R
(d) λ = 2, μ ∈ R

Ans. a

 Given, system of linear equations

4x + λy + 2z = 0

2x − y + z = 0

μx + 2y + 3z = 0

For non-trivial solution, Δ = 0

⇒ 4(−3 − 2) − λ(6 − μ) + 2(4 + μ) = 0

⇒ −λ(6 − μ) − 2(6 − μ) = 0

⇒ (6 − μ)(λ + 2) = 0

⇒ λ = −2 and μ ∈ R or μ = 6 and λ ∈ R.

Q.78. Let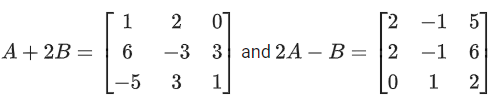If Tr(A) denotes the sum of all diagonal elements of the matrix A, then Tr(A) − Tr(B) has value equal to        (JEE Main 2021)
(a) 1
(b) 2
(c) 0
(d) 3

Ans. b

Similarly, 

Tr(A) − Tr(B) = 1 − (−1) = 2

Q.79. The solutions of the equation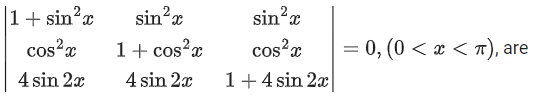        (JEE Main 2021)
(a)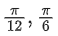
(b)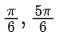
(c)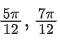
(d)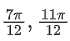

Ans. d
By using C₁ → C₁ − C₂ and C₃ → C₃ − C₂ we get

Expanding by R₁ we get
1(1 + cos²x + 4sin⁡2x) − sin²x(−1) = 0
⇒ 2 + 4sin⁡2x = 0
⇒ sin⁡2x = −1/2
⇒ 2x = nπ + (−1)ⁿ(−π/6), n ∈ Z

Q.80. If x, y, z are in arithmetic progression with common difference d, x ≠ 3d, and the determinant of the matrix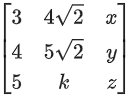is zero, then the value of k² is:        (JEE Main 2021)
(a) 72
(b) 12
(c) 36
(d) 6

Ans. a

R₁ → R₁ + R₃ − 2R₂

⇒ (k − 6√2)(4z − 5y) = 0
⇒ k = 6√2 or 4z = 5y (Not possible ∵ x, y, z in A.P.)
So, k² = 72
∴ Option (A) 

Q.81. If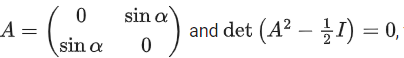then a possible value of α is:        (JEE Main 2021)
(a) π/4
(b) π/6
(c) π/2
(d) π/3

Ans. a

Q.82. The system of equations kx + y + z = 1, x + ky + z = k and x + y + zk = k² has no solution if k is equal to:        (JEE Main 2021)
(a) 0
(b) −1
(c) −2
(d) 1

Ans. c

⇒ k(k² − 1) − (k − 1) + (1 − k) = 0
⇒ (k − 1)(k² + k − 1 − 1) = 0
⇒ (k − 1)(k² + k − 2) = 0
⇒ (k − 1)(k − 1)(k + 2) = 0
⇒ k = 1, k = −2
for k = 1 equation identical so k = −2 for no solution. 

Q.83. Let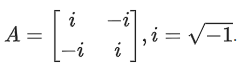 Then, the system of linear equations

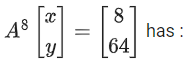       (JEE Main 2021)
(a) Exactly two solutions 
(b) Infinitely many solutions
(c) A unique solution 
(d) No solution

Ans. d




⇒ 128(x − y) = 8
⇒ x − y = 1/16 .... (1)
and 128(−x + y) = 64 ⇒ x − y = −1/2 .... (2)
⇒ No solution (from eq. (1) & (2))

Q.84. Consider the following system of equations:
x + 2y − 3z = a
2x + 6y − 11z = b
x − 2y + 7z = c,
where a, b and c are real constants. Then the system of equations:       (JEE Main 2021)
(a) has no solution for all a, b and c
(b) has a unique solution when 5a = 2b + c
(c) has infinite number of solutions when 5a = 2b + c
(d) has a unique solution for all a, b and c

Ans. c

= 20 − 2(25) −3(−10)
= 20 − 50 + 30 = 0

= 20a − 2(7b + 11c) −3(−2b − 6c)
= 20a − 14b − 22c + 6b +18c
= 20a − 8b − 4c
= 4(5a − 2b − c)

= 7b + 11c − a(25) −3(2c − b)
= 7b + 11c − 25a − 6c + 3b
= −25a + 10b + 5c
= −5(5a − 2b − c)

= 6c + 2b − 2(2c − b) − 10a
= −10a + 4b + 2c
= −2(5a − 2b − c)
for infinite solution
D = D₁ = D₂ = D₃ = 0
⇒ 5a = 2b + c 

Q.85. The value of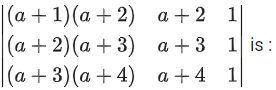       (JEE Main 2021)
(a) −2
(b) 0
(d) (a + 2)(a + 3)(a + 4)
(d) (a + 1)(a + 2)(a + 3)

Ans. a

R₂ → R₂ − R₁ and R₃ → R₃ − R₁

= 4(a + 2) − 4a − 10
= 4a + 8 − 4a − 10 = −2

Q.86. Let A be a symmetric matrix of order 2 with integer entries. If the sum of the diagonal elements of A² is 1, then the possible number of such matrices is:       (JEE Main 2021)
(a) 6
(b) 4
(c) 1
(d) 12

Ans. b


= a² + 2b² + c² = 1
a = 1, b = 0, c = 0
a = 0, b = 0, c = 1
a = −1, b = 0, c = 0
c = −1, b = 0, a = 0

Q.87. The following system of linear equations
2x + 3y + 2z = 9
3x + 2y + 2z = 9
x − y + 4z = 8       (JEE Main 2021)
(a) does not have any solution
(b) has a solution (α, β, γ) satisfying α + β² + γ³ = 12
(c) has a unique solution
(d) has infinitely many solutions

Ans. c



Unique solution: (0, 1, 2) 

Q.88. If for the matrix,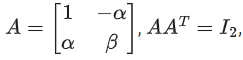then the value of α⁴ + β⁴ is:       (JEE Main 2021)
(a) 3
(b) 2
(c) 1
(d) 4 

Ans. c

1 + α² = 1
α² = 0
α² + β² = 1
β² = 1
α⁴ = 0
β⁴ = 1
α⁴ + β⁴ = 1 

Q.89. Let A be a 3 × 3 matrix with det(A) = 4. Let R_i denote the i^th row of A. If a matrix B is obtained by performing the operation R₂ → 2R₂ + 5R₃ on 2A, then det(B) is equal to:       (JEE Main 2021)
(a) 64
(b) 16
(c) 128
(d) 80

Ans. a

R₂ → 2R₂ + 5R₃

R₂ → R₂ − 5R₃


= 16 × 4
= 64

Q.90. For the system of linear equations:
x − 2y = 1, x − y + kz = −2, ky + 4z = 6, k ∈ R,
consider the following statements:
(A) The system has unique solution if k ≠ 2, k ≠ −2.
(B) The system has unique solution if k = −2
(C) The system has unique solution if k = 2
(D) The system has no solution if k = 2
(E) The system has infinite number of solutions if k ≠ −2.
Which of the following statements are correct?       (JEE Main 2021)
(a) (B) and (E) only
(b) (C) and (D) only
(c) (A) and (E) only
(d) (A) and (D) only

Ans. d
x − 2y + 0.z = 1
x − y + kz = −2
0.x + ky + 4z = 6

For unique solution 4 − k² ≠ 0
⇒ k ≠ ± 2
For k = 2:
x − 2y + 0.z = 1
x − y + 2z = −2
0.x + 2y + 4z = 6

Δx = −48 ≠ 0
For k = 2, Δx ≠ 0
∴ For K = 2; The system has no solution.

Q.91. Let A and B be 3 × 3 real matrices such that A is symmetric matrix and B is skew-symmetric matrix. Then the system of linear equations (A²B² − B²A²) X = O, where X is a 3 × 1 column matrix of unknown variables and O is a 3 × 1 null matrix, has:       (JEE Main 2021)
(a) no solution
(b) exactly two solutions
(c) infinitely many solutions
(d) a unique solution

Ans. c
A^T = A, B^T = −B
Let A²B² − B²A² = P
P^T = (A²B² − B²A²)^T = (A²B²)^T − (B²A²)^T
= (B²)^T (A²)^T − (A²)^T (B²)^T
= B²A² − A²B²
⇒ P is skew-symmetric matrix

∴ ay + bz = 0 ..... (1)
−ax + cz = 0 .... (2)
−bx −cy = 0 ..... (3)
From equation 1, 2, 3
Δ = 0 & Δ₁ = Δ₂ = Δ₃ = 0
∴ equation have infinite number of solution

Q.92. The system of linear equations
3x - 2y - kz = 10
2x - 4y - 2z = 6
x + 2y - z = 5m
is inconsistent if:       (JEE Main 2021)
(a) k ≠ 3, m ∈ R
(b) k = 3, m ≠ 4/5
(c) k = 3, m = 4/5
(d) k ≠ 3, m ≠ 4/5

Ans. b

3(4 + 4) + 2(−2 + 2) − k(4 + 4) = 0
⇒ k = 3

10(4 + 4) + 2(−6 + 10m) − 3(12 + 20m) ≠ 0
80 − 12 + 20m − 36 − 60m ≠ 0
40m ≠ 32 ⇒ m ≠ 4/5

3(−6 + 10m) − 10(−2 + 2) − 3(10m − 6) ≠ 0
−18 + 30m − 30m + 18 ≠ 0 ⇒ 0

3(−20m − 12) + 2(10m − 6) + 10(4 + 4) − 40m + 32 ≠ 0 ⇒ m ≠ 4/5

Q.93. The number of elements in the set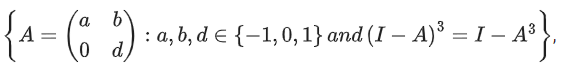where I is 2 × 2 identity matrix, is:       (JEE Main 2021)

Ans. 8
(I − A)³ = I³ − A³ − 3A(I − A) = I − A³
⇒ 3A(I − A) = 0 or A² = A

⇒ a² = a, b(a + d − 1) = 0, d² = d
If b ≠ 0, a + d = 1 ⇒ 4 ways
If b = 0, a = 0, 1 & d = 0, 1 ⇒ 4 ways
⇒ Total 8 matrices 

Q.94. If the system of linear equations
2x + y − z = 3
x − y − z = α
3x + 3y + βz = 3
has infinitely many solution, then α + β − αβ is equal to _____________.        (JEE Main 2021)

Ans. 5
2 × (i) − (ii) − (iii) gives :
− (1 + β)z = 3 − α
For infinitely many solution
β + 1 = 0 = 3 − α ⇒ (α, β) = (3, −1)
Hence, α + β − αβ = 5 

Q.95. Let A be a 3 × 3 real matrix. If det(2Adj(2 Adj(Adj(2A)))) = 2⁴¹, then the value of det(A²) equal __________.         (JEE Main 2021)

Ans. 4
adj (2A) = 2² adjA
⇒ adj(adj (2A)) = adj(4 adjA) = 16 adj (adj A)
= 16 | A | A
⇒ adj (32 | A | A) = (32 | A |)² adj A
12(32| A |)² |adj A | = 2³ (32 | A |)⁶ | adj A |
2³ . 2³⁰ | A |⁶ . | A |² = 2⁴¹
| A |⁸ = 2⁸ ⇒ | A | = ±2
| A |² = | A |² = 4 

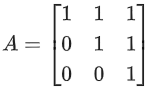Q.96. If and M = A + A² + A³ + ....... + A²⁰, then the sum of all the elements of the matrix M is equal to _____________.          (JEE Main 2021)

Ans. 2020

So, required sum 

= 60 + 420 + 105 + 35 × 41 = 2020

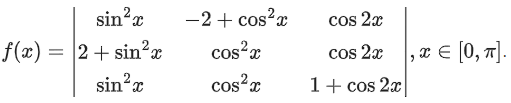Q.97. LetThen the maximum value of f(x) is equal to ______________.          (JEE Main 2021)

Ans. 6

= −2(cos²x) + 2(2 + 2cos⁡2x + sin²x)
= 4 + 4cos⁡2x − 2(cos²x − sin²x)

⇒ f(x)_max = 4 + 2 = 6 

Q.98. For real numbers α and β, consider the following system of linear equations:
x + y − z = 2, x + 2y + αz = 1, 2x − y + z = β. If the system has infinite solutions, then α + β is equal to ______________.          (JEE Main 2021)

Ans. 5
For infinite solutions
Δ = Δ₁ = Δ₂ = Δ₃ = 0 

Δ = 3(2 + α) = 0
⇒ α = −2 

1(1 + 2β) −2(1 + 4) − (β − 2) = 0
β − 7 = 0
β = 7
∴ α + β = 5

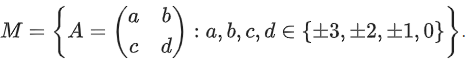Q.99. LetDefine f : M → Z, as f(A) = det(A), for all A ∈ M, where z is set of all integers. Then the number of A∈M such that f(A) = 15 is equal to _____________.          (JEE Main 2021)

Ans. 16
| A | = ad − bc = 15
where a, b, c, d ∈ {±3, ±2, ±1, 0}
Case I ad = 9 & bc = −6
For ad possible pairs are (3, 3), (−3, −3)
For bc possible pairs are (3, −2), (−3, 2), (−2, 3), (2, −3)
So total matrix = 2 × 4 = 8
Case II ad = 6 & bc = −9
Similarly total matrix = 2 × 4 = 8
⇒ Total such matrices are = 16 

Q.100. Let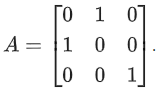 Then the number of 3 × 3 matrices B with entries from the set {1, 2, 3, 4, 5} and satisfying AB = BA is ____________.          (JEE Main 2021)

Ans. 3125

∵ AB = BA

⇒ d = b, e = a, f = c, g = h

No. of ways of selecting a, b, c, g, i
= 5 × 5 × 5 × 5 × 5
= 5⁵ = 3125
∴ No. of matrices B = 3125 

Q.101. Let A = {a_ij} be a 3 × 3 matrix,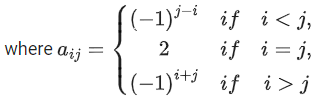

then det(3Adj(2A⁻¹)) is equal to _____________.          (JEE Main 2021)

Ans. 108

|A| = 4
det(3adj(2A⁻¹))
= 3³|adj(2a⁻¹)|

Q.102. Let a, b, c, d in arithmetic progression with common difference λ. If  then value of λ² is equal to ________________.          (JEE Main 2021)

Ans. 1

C₂ → C₂ − C₃

R₂ → R₂ − R₁, R₃ → R₃ − R₁

⇒ 1(4λ² − 4λ² + 2λ) = 2
⇒ λ² = 1

Q.103. Let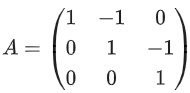and B = 7A²⁰ − 20A⁷ + 2I, where I is an identity matrix of order 3 × 3. If B = [b_ij], then b₁₃ is equal to _____________.         (JEE Main 2021)

Ans. 910


B = 7A²⁰ − 20A⁷ + 2I
= 7(I + C)²⁰ + 20(I + C)⁷ + 2I
= 7(I + 20C + ²⁰C₂C₂) − 20(I + 7C + ⁷C₂C₂) + 2I
So b₁₃ = 7 × ²⁰C₂C² − 20 × ⁷C₂ = 910

Q.104. Let I be an identity matrix of order 2 × 2 and P =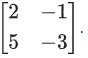Then the value of n ∈ N for which Pⁿ = 5I − 8P is equal to ____________.         (JEE Main 2021) 

Ans. 6

⇒ λ² + λ − 1 = 0
⇒ P² + P − I = 0
⇒ P² = I − P
⇒ P⁴ = I + P² − 2P
⇒ P⁴ = 2I − 3P
Now, P⁴ . P² = (2I − 3P)(I − P) = 2I − 5P + 3P²
⇒ P⁶ = 5I − 8P
So n = 6 

Q.105. If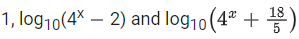(4x+185) are in arithmetic progression for a real number x, then the value of the determinant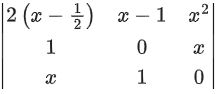is equal to:         (JEE Main 2021) 

Ans. 2


(4^x)² + 4 − 4.4^x = 10.4^x + 36
(4^x)² − 14.4^x − 32 = 0
(4^x)² + 2.4^x − 16.4^x − 32 = 0
4^x(4^x + 2) − 16.(4^x + 2) = 0
(4^x + 2)(4^x − 16) = 0
4^x = -2 (Not Possible)
Or 4^x = 16
⇒ x = 2

= 3(−2) − 1(0 − 4) + 4(1 − 0)
= −6 + 4 + 4 = 2

Q.106. Let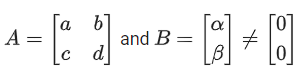such that AB = B and a + d = 2021, then the value of ad − bc is equal to ___________.         (JEE Main 2021) 

Ans. 2020

AB = B

α(a − 1) = −bβ and cα = β(1 − d)


−bc = (a − 1)(1 − d)
−bc = a − ad − 1 + d
ad − bc = a + d − 1
= 2021 - 1 = 2020

Q.107. If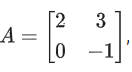then the value of det(A⁴) + det(A¹⁰ − (Adj(2A))¹⁰) is equal to _____________.         (JEE Main 2021) 

Ans. 16






|A¹⁰ − adj(2A)¹⁰| = 0
∴ det(A⁴) + det(A¹⁰ − (Adj(2A))¹⁰)
= 16 + 0 = 16 

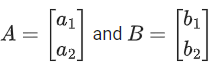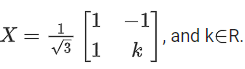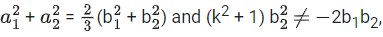Q.108. Letbe two 2 × 1 matrices with real entries such that A = XB, whereIf then the value of k is __________.         (JEE Main 2021) 

Ans. 1
XB = A



Comparing both sides, We get 

⇒ k² = 1
⇒ k = ± 1 ......(1)
and 2/3(k − 1)=0 ⇒ k = 1 ....(2)
From (1) and (2),
k = 1 

Q.109. The total number of 3 × 3 matrices A having entries from the set {0, 1, 2, 3} such that the sum of all the diagonal entries of AA^T is 9, is equal to _____________.         (JEE Main 2021) 

Ans. 766
 
Tr(AA^T) = x² + y² + z² + a² + b² + c² + d² + e² + f² = 9
Case-I: Nine ones = 1 case
Case-II: 8 zeroes and one entry is 3 = 9!/8!=9 cases
Case-III: Two 2’s, one 1’s and 6 zeroes == 63 × 4 = 252
Case IV: one 2, five 1, rest 0= 63 × 8 = 504
∴ Total cases = 9 + 252 + 504 + 1 = 766

Q.110.

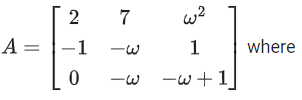
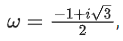and I₃ be the identity matrix of order 3. If the
determinant of the matrix (P⁻¹AP−I₃)² is αω², then the value of α is equal to ______________.         (JEE Main 2021) 

Ans. 36
 |P⁻¹AP^−I|²
= |(P⁻¹AP − I)(P⁻¹AP⁻¹)²|
= |P⁻¹APP⁻¹AP − 2P⁻¹AP + I|
= |P⁻¹A²P − 2P⁻¹AP + P⁻¹IP|
= |P⁻¹(A² − 2A + I)P|
= |P⁻¹(A − I)²P|
= |P⁻¹||A − I|²|P|
= |A − I|²

= (1(ω(ω + 1) + ω) − 7ω + ω².ω)²
= (ω² + 2ω − 7ω + 1)²
= (ω² − 5ω + 1)²
= (−6ω)²
= 36ω²
∴ αω² = 36ω2
⇒ α = 36

Q.111. If the matrix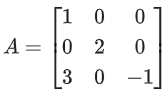satisfies the equation 

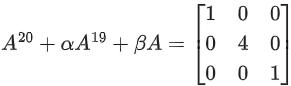for some real numbers α and β, then β − α is equal to ___________.         (JEE Main 2021) 

Ans. 4




⇒ α + β = 0 and 2²⁰ + α2¹⁹ + 2β = 4
⇒ 2²⁰ + α(2¹⁹ − 2) = 4

⇒ β = 2
∴ β − α = 4

Q.112. If the system of equations
kx + y + 2z = 1
3x − y − 2z = 2
−2x −2y −4z = 3
has infinitely many solutions, then k is equal to __________.         (JEE Main 2021)

Ans. 21
D = 0

⇒ k (4 − 4) − 1 (− 12 − 4) + 2 (− 6 − 2)
⇒ 16 − 16 = 0
Also, D₁ = D₂ = D₃ = 0

⇒ k(−8 + 6) − 1(− 12 − 4) + 2(9 + 4) = 0
⇒ − 2k + 16 + 26 = 0
⇒ 2k = 42
⇒ k = 21

Q.113. Let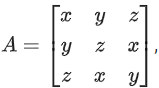where x, y and z are real numbers such that x + y + z > 0 and xyz = 2. If A² = I₃, then the value of x³ + y³ + z³ is ____________.         (JEE Main 2021)

Ans. 7

∴ |A| = (x³ + y³ + z³ − 3xyz)
Given A² = I₃
|A²| = 1
∴ (x³ + y³ + z³ − 3xyz)2 = 1
⇒ x³ + y³ + z³ − 3xyz = 1 only as (x + y + z > 0)
⇒ x³ + y³ + z³ = 6 + 1 = 7

Q.114. Ifand

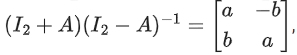then 13(a² + b²) is equal to         (JEE Main 2021)

Ans. 13 


⇒ (1 + A)(I − A)⁻¹


∴ a² + b² = 1
⇒ 13(a² + b²) = 13

Q.115. Let M be any 3 × 3 matrix with entries from the set {0, 1, 2}. The maximum number of such matrices, for which the sum of diagonal elements of M^TM is seven, is ________.         (JEE Main 2021)

Ans. 540

a² + b² + c² + d² + e² + f² + g² + h² + i² = 7
Case I: Seven (1's) and two (0's)
Number of such matrices = ⁹C₂ = 36
Case II: One (2) and three (1's) and five (0's)
Number of such matrices ==504
∴ Total = 540

Q.116. Letwhere α ∈ R. Suppose Q = [ q_ij] is a matrix satisfying PQ = kl₃ for some non-zero k ∈ R.
If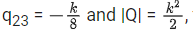then a² + k² is equal to ______.          (JEE Main 2021)

Ans. 17



⇒ 2(3α + 4) = 5 + 3α
3α = −3 ⇒ α = −1

⇒ (20 + 12α) = 2k ⇒ 8 = 2k ⇒ k = 4