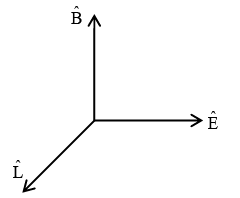
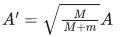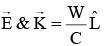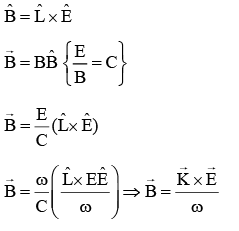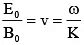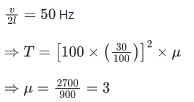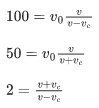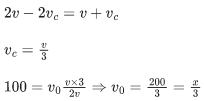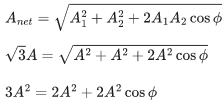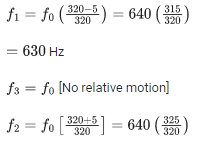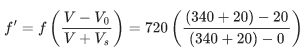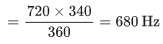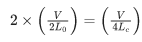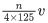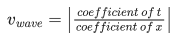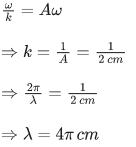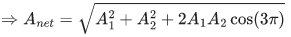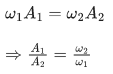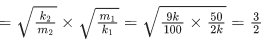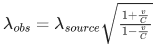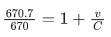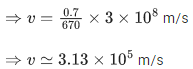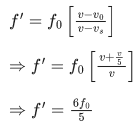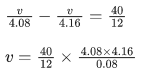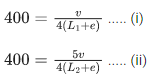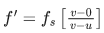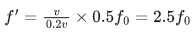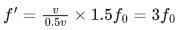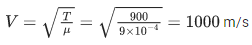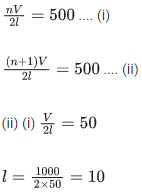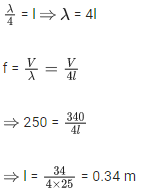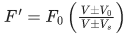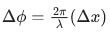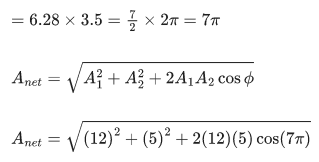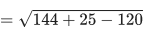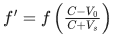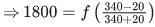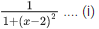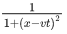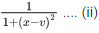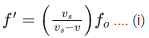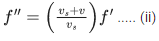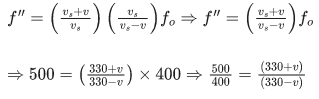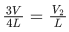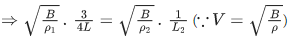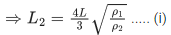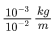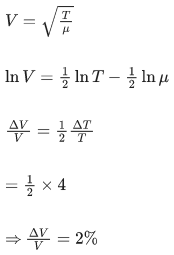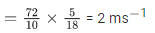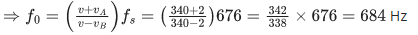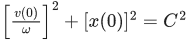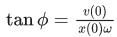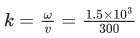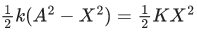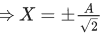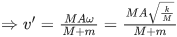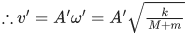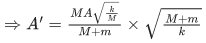Q.1. In represent electric field and propagation vectors of the EM waves in vacuum, then magnetic field vector is given by : (JEE Main 2023)
represent electric field and propagation vectors of the EM waves in vacuum, then magnetic field vector is given by : (JEE Main 2023)
(ω - angular frequency):
(a) 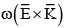
(b) 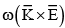
(c) 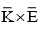
(d) 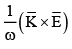
Ans. d
Q.2. The electric field and magnetic field components of an electromagnetic wave going through vacuum is described by
Ex = E0sin(kz − ωt)
By = Bosin(kz − ωt)
Then the correct relation between Eo and Bo is given by (JEE Main 2023)
(a) E0 B0 = ωk
(b) E0 = kB0
(c) kEo = ωBo
(d) ωEO = kBO
Ans. c
by theory of EM wave
Q.3. Match List I with List II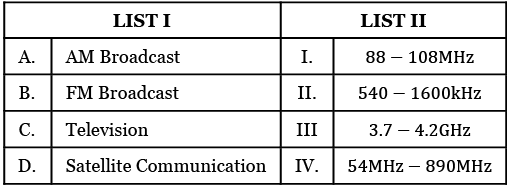
Choose the correct answer from the options given below: (JEE Main 2023)
(a) A-II, B-I, C-IV, D-III
(b) A-I, B-III, C-II, D-IV
(c) A-IV, B-III, C-I, D-II
(d) A-II, B-III, C-I, D-IV
Ans. a
by concept of AM & FM freq. range
Q.4. On a frictionless horizontal plane, a bob of mass m = 0.1 kg is attached to a spring with natural length l0 = 0.1 m. The spring constant is k1 = 0.009Nm−1 when the length of the spring l > l0 and is k2 = 0.016Nm−1 when l < l0. Initially the bob is released from l = 0.15 m. Assume that Hooke's law remains valid throughout the motion. If the time period of the full oscillation is T = (nπ)s, then the integer closest to n is __________. (JEE Advanced 2022)
Ans. 6
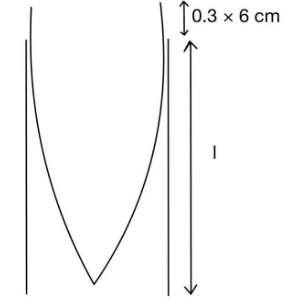
Q.5. A wire of length 30 cm, stretched between rigid supports, has it's nth and (n + 1)th harmonics at 400 Hz and 450 Hz, respectively. If tension in the string is 2700 N, it's linear mass density is ____________ kg/m. (JEE Main 2022)
Ans. 3
Q.6. When a car is approaching the observer, the frequency of horn is 100 Hz. After passing the observer, it is 50 Hz. If the observer moves with the car, the frequency will be x/3 Hz where x=__________. (JEE Main 2022)
Ans. 200
⇒ x = 200.
Q.7. Two waves executing simple harmonic motions travelling in the same direction with same amplitude and frequency are superimposed. The resultant amplitude is equal to the √3 times of amplitude of individual motions. The phase difference between the two motions is ___________ (degree). (JEE Main 2022)
Ans. 60°
cos∅ = 1/2
∅ = 60°
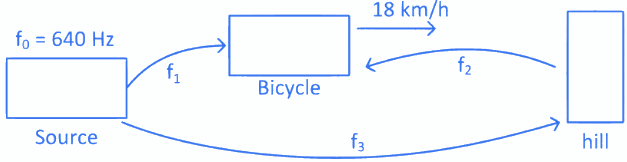
Q.8. An observer is riding on a bicycle and moving towards a hill at 18kmh−1. He hears a sound from a source at some distance behind him directly as well as after its reflection from the hill. If the original frequency of the sound as emitted by source is 640 Hz and velocity of the sound in air is 320 m/s, the beat frequency between the two sounds heard by observer will be _____________ Hz. (JEE Main 2022)
Ans. 20
= 650
Beat frequency =f2−f1
= 650−630 = 20 Hz.
Q.9. An employee of a factory moving away from his workplace by a car listens to the siren of the factory. He drives the car at the speed of 72 kmh−1 in the direction of wind which is blowing at 72 kmh−1 speed. Frequency of siren is 720 Hz. The employee hears an apparent frequency of ____________ Hz.
(Assume speed of sound to be 340 ms−1) (JEE Main 2022)
Ans. 680
Here, the apparent frequency is given by
Q.10. Two travelling waves of equal amplitudes and equal frequencies move in opposite directions along a string. They interfere to produce a stationary wave whose equation is given by y=(10cosπxsin(2πt/T)) cm.
The amplitude of the particle at x=4/3 cm will be ___________ cm. (JEE Main 2022)
Ans. 5
A=|10cos(πx)|
At x=4/3
A=|10cos(π×(4/3))|
= |− 5 cm|
∴ Amp = 5 cm
Q.11. The first overtone frequency of an open organ pipe is equal to the fundamental frequency of a closed organ pipe. If the length of the closed organ pipe is 20 cm. The length of the open organ pipe is _____________ cm. (JEE Main 2022)
Ans. 80
⇒ L0 = 4Lc
= 4 × 20
= 80 cm
Q.12. A set of 20 tuning forks is arranged in a series of increasing frequencies. If each fork gives 4 beats with respect to the preceding fork and the frequency of the last fork is twice the frequency of the first, then the frequency of last fork is _________ Hz. (JEE Main 2022)
Ans. 152
Given v20 = 2v1
Also v20 = 4×19+v1
So v20 = 152 Hz
Q.13. A tunning fork of frequency 340 Hz resonates in the fundamental mode with an air column of length 125 cm in a cylindrical tube closed at one end. When water is slowly poured in it, the minimum height of water required for observing resonance once again is ___________ cm.
(Velocity of sound in air is 340 ms−1) (JEE Main 2022)
Ans. 50
Given 340 =⇒ n = 5
So λ = 100 cm
So minimum height is (λ/2) = 50 cm.
Q.14. In the wave equation y = 0.5sin(2π/λ)(400t−x)m the velocity of the wave will be: (JEE Main 2022)
(a) 200 m/s
(b) 200√2 m/s
(c) 400 m/s
(d) 400√2 m/s
Ans. c
= 400/1 = 400 m/s
Q.15. A transverse wave is represented by y=2sin(ωt−kx)cm. The value of wavelength (in cm) for which the wave velocity becomes equal to the maximum particle velocity, will be : (JEE Main 2022)
(a) 4π
(b) 2π
(c) π
(d) 2
Ans. a
Q.16. Which of the following equations correctly represents a travelling wave having wavelength λ = 4.0 cm, frequency v = 100 Hz and travelling in positive x-axis direction? (JEE Main 2022)
(a) y=Asin[(0.50πcm−1)x−(100πs−1)t]
(b) y=Asin2π[(0.25cm−1)x−(50s−1)t]
(c) y=Asin[((2π/4)cm−1)x−((2π/100)s−1)t]
(d) y=Asinπ[(0.5cm−1)x−(200s−1)t]
Ans. d
We know, equation of wave travelling in positive x-direction is -
y = Asin(kx−wt)
where k = (2π/λ)
and w = 2πf
Here given λ = 4 cm and frequency (f) = 100 Hz
∴ k=(2π/4)=0.5π cm−1 and w=2π×100=200π s−1
∴ Equation of travelling wave,
y=Asin(0.5πx−200πt)
Q.17. The equations of two waves are given by :
y1 = 5 sin 2π(x - vt) cm
y2 = 3 sin 2π(x − vt + 1.5) cm
These waves are simultaneously passing through a string. The amplitude of the resulting wave is : (JEE Main 2022)
(a) 2 cm
(b) 4 cm
(c) 5.8 cm
(d) 8 cm
Ans. a
y1=5sin(2πx−2πvt)
y2=3sin(2πx−2πvt+3π)
⇒ Phase difference = 3
⇒ Anet = 2 cm.
Q.18. Two massless springs with spring constants 2 k and 9 k, carry 50 g and 100 g masses at their free ends. These two masses oscillate vertically such that their maximum velocities are equal. Then, the ratio of their respective amplitudes will be : (JEE Main 2022)
(a) 1 : 2
(b) 3 : 2
(c) 3 : 1
(d) 2 : 3
Ans. b
Q.19. For a specific wavelength 670 nm of light coming from a galaxy moving with velocity v, the observed wavelength is 670.7 nm. The value of v is : (JEE Main 2022)
(a) 3 × 108 ms−1
(b) 3 × 1010 ms−1
(c) 3.13 × 105 ms−1
(d) 4.48 × 105 ms−1
Ans. c
For v<<C,
Q.20. An observer moves towards a stationary source of sound with a velocity equal to one-fifth of the velocity of sound. The percentage change in the frequency will be : (JEE Main 2022)
(a) 20%
(b) 10%
(c) 5%
(d) 0%
Ans. a
⇒ % change = 20
Q.21. If a wave gets refracted into a denser medium, then which of the following is true? (JEE Main 2022)
(a) wavelength, speed and frequency decreases.
(b) wavelength increases, sped decreases and frequency remains constant.
(c) wavelength and speed decreases but frequency remains constant.
(d) wavelength, speed and frequency increases.
Ans. c
Frequency is independent of medium. For denser medium, wavelength and speed both would decrease.
Q.22. The velocity of sound in a gas, in which two wavelengths 4.08 m and 4.16 m produce 40 beats in 12s, will be : (JEE Main 2022)
(a) 282.8 ms−1
(b) 175.5 ms−1
(c) 353.6 ms−1
(d) 707.2 ms-1
Ans. d
=707.2 m/s-1
Q.23. A longitudinal wave is represented by x=10sin2π(nt−(x/λ)) cm. The maximum particle velocity will be four times the wave velocity if the determined value of wavelength is equal to : (JEE Main 2022)
(a) 2π
(b) 5π
(c) π
(d) 5π/2
Ans. b
Particle velocity =
⇒ Maximum particle velocity =(2πn)(10)
⇒(2πn)(10)=(nλ)(4)⇒ λ = 5π
Q.24. In an experiment to determine the velocity of sound in air at room temperature using a resonance tube, the first resonance is observed when the air column has a length of 20.0 cm for a tuning fork of frequency 400 Hz is used. The velocity of the sound at room temperature is 336 ms−1. The third resonance is observed when the air column has a length of _____________ cm. (JEE Main 2022)
Ans. 104
⇒ L1+e=λ/4=21 cm
L2+e=5λ/4=105 cm
⇒ e = 1 cm & L2 = 104 cm
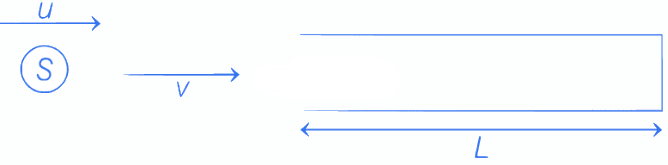
Q.25. A source, approaching with speed u towards the open end of a stationary pipe of length L, is emitting a sound of frequency fs. The farther end of the pipe is closed. The speed of sound in air is v and f0 is the fundamental frequency of the pipe. For which of the following combination(s) of u and fs, will the sound reaching the pipe lead to a resonance? (JEE Advanced 2021)
(a) u = 0.8v and fs = f0
(b) u = 0.8v and fs = 2f0
(c) u = 0.8v and fs = 0.5f0
(d) u = 0.5v and fs = 1.5f0
Ans. a and d
Natural frequency of closed pipe,
f = (2n + 1)f0
f0 is fundamental frequency
n = 0, 1, 2___
Frequency of source received by pipe,
For resonance,
f′=f
If u = 0.8v, fs = f0
For n = 2 pipe can be in resonance
Hence, option (a) is correct.
If u = 0.8v, fs = 2f0
If u = 0.8v, fs = 0.5f0
Not possible.
If u = 0.5v, fs = 1.5 f0
For n = 1 f = 3f0
Pipe can be in resonance.
Hence, option (d) is correct.
Q.26. A wire having a linear mass density 9.0 × 10−4 kg/m is stretched between two rigid supports with a tension of 900 N. The wire resonates at a frequency of 500 Hz. The next higher frequency at which the same wire resonates is 550 Hz. The length of the wire is ____________ m. (JEE Main 2021)
Ans. 10
μ=9.0×10−4(kg/m)
T = 900 N
f1 = 500 Hz
f = 550
Q.27. A tuning fork is vibrating at 250 Hz. The length of the shortest closed organ pipe that will resonate with the tuning fork will be __________ cm. (Take speed of sound in air as 340 ms−1) (JEE Main 2021)
Ans. 34
l = 34 cm
Q.28. Two cars X and Y are approaching each other with velocities 36 km/h and 72 km/h respectively. The frequency of a whistle sound as emitted by a passenger in car X, heard by the passenger in car Y is 1320 Hz. If the velocity of sound in air is 340 m/s, the actual frequency of the whistle sound produced is ____ Hz. (JEE Main 2021)
Ans. 1210
Image
Vx = 36 km/hr = 10 m/s
Vy = 72 km/hr = 20 m/s
by doppler's effect⇒F0=1210 Hz
Q.29. Two waves are simultaneously passing through a string and their equations are :
y1 = A1 sin k(x − vt), y2 = A2 sin k(x − vt + x0). Given amplitudes A1 = 12 mm and A2 = 5 mm, x0 = 3.5 cm and wave number k = 6.28 cm−1. The amplitude of resulting wave will be ____ mm. (JEE Main 2021)
Ans. 7
y1 = A1 sin k(x − vt)
y1 = 12 sin 6.28 (x − vt)
y2 = 5 sin 6.28 (x − vt + 3.5)
=K(Δx)
Q.30. Two travelling waves produces a standing wave represented by equation,
y = 1.0 mm cos(1.57 cm−1) x sin(78.5 s−1)t.
The node closest to the origin in the region x > 0 will be at x = ____ cm. (JEE Main 2021)
Ans. 1
For node
cos(1.57 cm−1)x = 0
(1.57 cm−1)x = π/2
x =cm = 1 cm.
Q.31. A source and a detector move away from each other in absence of wind with a speed of 20 m/s with respect to the ground. If the detector detects a frequency of 1800 Hz of the sound coming from the source, then the original frequency of source considering speed of sound in air 340 m/s will be ____ Hz. (JEE Main 2021)
Ans. 2025
Image
f = 2025 Hz.
Q.32. The amplitude of wave disturbance propagating in the positive x-direction is given by y = 1/(1+x)2 at time t = 0 and y = 1/1+(x−2)2 at t = 1 s, where x and y are in metres. The shape of wave does not change during the propagation. The velocity of the wave will be ___________ m/s. (JEE Main 2021)
Ans. 2
As per question,
at t = 0, y =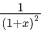
and at t = 1 s, y =
As we know,
At t = t s, y =
So, at t = 1 s, y =
On comparing Eqs. (i) and (ii), we get
v = 2 ms−1
Hence, the velocity of the wave will be 2 m/s.
Q.33. The frequency of a car horn encountered a change from 400 Hz to 500 Hz, when the car approaches a vertical wall. If the speed of sound is 330 m/s. Then the speed of car is ___________ km/h. (JEE Main 2021)
Ans. 132
∵ Since, frequency received by the wall,
where, vs = velocity of sound in air, v = velocity of car and fo = observed frequency of sound.
Reflected frequency received by man is
From Eqs. (i) and (ii), we get
⇒ 5(330−v) = 4(330+v) ⇒1650−5v = 1320+4v
⇒ 9v = 330 ⇒ v = (330/9) m/s
or v = (330/9) x (18/5) = 132 km/h.
Q.34. A closed organ pipe of length L and an open organ pipe contain gases of densities ρ1 and ρ2 respectively. The compressibility of gases are equal in both the pipes. Both the pipes are vibrating in their first overtone with same frequency. The length of the open pipe is 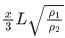 where x is ___________. (Round off to the Nearest Integer) (JEE Main 2021)
where x is ___________. (Round off to the Nearest Integer) (JEE Main 2021)
Ans. 4
First overtone of open pipe = v2/L2
First overtone of closed pipe at one end = 3v/4L
As per question,
According to question, the length of the open pipe is...(ii)
Comparing Eqs. (i) and (ii), we get x = 4.
Q.35. The mass per unit length of a uniform wire is 0.135 g/cm. A transverse wave of the form y = − 0.21 sin (x + 30t) is produced in it, where x is in meter and t is in second. Then, the expected value of tension in the wire is x × 10−2 N. Value of x is _________. (Round off to the nearest integer) (JEE Main 2021)
Ans. 1215
μ=0.135 gm/cm
μ=0.135 x
y = −0.21 sin (x + 30t)
v= ω/K = 30/1 = 30 m/s
T = v2 × μ
T = (30)2 × 0.135 × 10−1
T = 900 × 0.135 × 10−1
T = 12.15 N
T = 1215 × 10−2 N
x = 1215
Q.36. The percentage increase in the speed of transverse waves produced in a stretched string if the tension is increased by 4%, will be __________%. (JEE Main 2021)
Ans. 2
Speed of transverse wave is
Q.37. Two cars are approaching each other at an equal speed of 7.2 km/hr. When they see each other, both blow horns having frequency of 676 Hz. The beat frequency heard by each driver will be ___________ Hz. [Velocity of sound in air is 340 m/s.] (JEE Main 2021)
Ans. 8
Given, vA = vB = 7.2 kmh−1
Frequency of source, fs = 676 Hz
Speed of sound in air, v = 340 ms−1
Let f0 be the frequency heard by each driver.
By using Doppler effect for A,
(v - vA)fs = (v + vB)f0
Now, beat frequency = f0−fs = 684−676 = 8 Hz.
Q.38. The motion of a mass on a spring, with spring constant K is as shown in figure.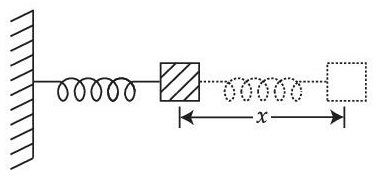
The equation of motion is given by
x(t) = A sinωt + B cosωt with ω = 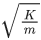
Suppose that at time t = 0, the position of mass is x(0) and velocity v(0), then its displacement can also be represented as x(t) = C cos(ωt − ϕ), where C and ϕ are : (JEE Main 2021)
(a) 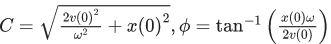
(b) 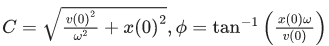
(c) 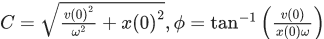
(d) 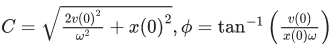
Ans. c
Ccosϕ=x(0)
tCωsinϕ=v(0)
Q.39. A sound wave of frequency 245 Hz travels with the speed of 300 ms−1 along the positive x-axis. Each point of the wave moves to and from through a total distance of 6 cm. What will be the mathematical expression of this travelling wave? (JEE Main 2021)
(a) Y(x, t) = 0.03 [ sin 5.1x − (0.2 × 103)t ]
(b) Y(x, t) = 0.03 [ sin 5.1x − (1.5 × 103)t ]
(c) Y(x, t) = 0.06 [ sin 5.1x − (1.5 × 103)t ]
(d) Y(x, t) = 0.06 [ sin 0.8x − (0.5 × 103)t ]
Ans. b
Y= Asin(kx−ωt)
A = 6/2 = 3cm = 0.03 m
ω = 2πf = 2π × 245
ω = 1.5 × 103
k = 5.1y = 0.03sin(5.1x - (1.5 x 103)t)
Q.40. For what value of displacement the kinetic energy and potential energy of a simple harmonic oscillation become equal ? (JEE Main 2021)
(a) x = A/2
(b) x = ± A
(c) x = ±A/√2
(d) x = 0
Ans. c
KE = PE
⇒ A2 - X2 = X2
⇒ 2X2 = A2
Q.41. A tuning fork A of unknown frequency produces 5 beats/s with a fork of known frequency 340 Hz. When fork A is field, the beat frequency decreases to 2 beats/s. What is the frequency of fork A? (JEE Main 2021)
(a) 335 Hz
(b) 345 Hz
(c) 338 Hz
(d) 342 Hz
Ans. a
Initially beat frequency = 5Hz
so, ρA = 340 ± 5 = 345 Hz, or 335 Hz
after filing frequency increases slightly so, new value of frequency of A > ρA
Now, beat frequency = 2Hz
⇒ new ρA = 340 ± 2 = 342 Hz, or 338 Hz
hence, original frequency of A is ρA = 335 Hz.
Q.42. A student is performing the experiment of resonance column. The diameter of the column tube is 6 cm. The frequency of the tuning fork is 504 Hz. Speed of the sound at the given temperature is 336 m/s. The zero of the metre scale coincides with the top end of the resonance column tube. The reading of the water level in the column when the first resonance occurs is : (JEE Main 2021)
(a) 13 cm
(b) 18.4 cm
(c) 16.6 cm
(d) 14.8 cm
Ans. d
∴ l+1.8 = λ/4
Also λ = v/f = 336/504
⇒ l+1.8 = (336)/(4 × 504)
⇒ l = 14.86 cm
Q.43. Which of the following equations represents a travelling wave? (JEE Main 2021)
(a) y = Aexcos(ωt − θ)
(b) y = Ae−x2(vt + θ)
(c) y = A sin (15x − 2t)
(d) y = A sinx cosωt
Ans. c
Y = F(x, t)
For travelling wave y should be linear function of x and t and they must exist as (x ± vt)
Y = A sin (15x − 2t) → linear function in x and t.
Q.44. In the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillations will be : (JEE Main 2021)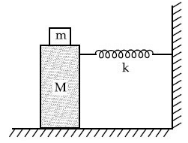
(a) 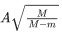
(b) 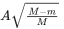
(c) 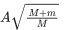
(d) 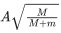
Ans. d
Given, initial amplitude = A
Velocity at mean position, v = Aω
Applying conservation of momentum at mean position, we get
M1v1 = M2v2
MAω = (M + m)v'