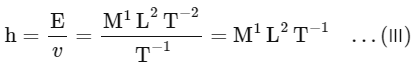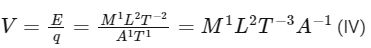[JEE Mains MCQs 2023]
Q1: The speed of a wave produced in water is given by v = λagbρc . Where λ, g and ρ are wavelength of wave, acceleration due to gravity and density of water respectively. The values of a, b and c respectively, are:
(a) 1/2 , 0 , 1/2
(b) 1, 1, 0
(c) 1, -1 , 0
(d) 1/2 , 1/2 , 0
Ans: (d)
v = λagbρc
using dimension formula
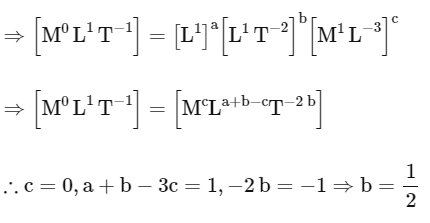
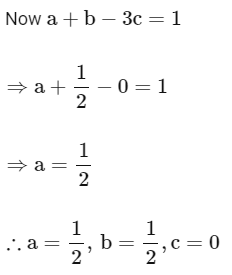
Q2: In the equation is pressure, Y is volume, R is universal gas constant and T is temperature. The physical quantity equivalent to the ratio a/b is:
is pressure, Y is volume, R is universal gas constant and T is temperature. The physical quantity equivalent to the ratio a/b is:
(a) Impulse
(b) Energy
(c) Pressure gradient
(d) Coefficient of viscosity
Ans: (b)
Given that, 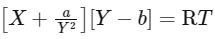
∴ X and a/Y2 have the same dimensions and Y and b have the same dimensions, let's analyze the dimensions of a/b.
Since X represents pressure, it has dimensions of [ML−1T− 2].
Since X and a/Y2 have the same dimensions, we have:
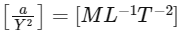
Then, the dimensions of a are:

Now, since Y and b have the same dimensions and Y represents volume, we have:
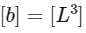
Now, let's find the dimensions of the ratio a/b:
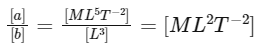
Indeed, the dimensions of a/b are [ML2T-2], which corresponds to the dimensions of energy.
Q3: A body of mass (5 ± 0.5) kg is moving with a velocity of (20 ± 0.4) m/s. Its kinetic energy will be
(a) (1000 ± 140) J
(b) (500 ± 0.14) J
(c) (1000 ± 0.14) J
(d) (500 ± 140) J
Ans: (a)
To find the kinetic energy of the body, we can use the formula:
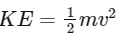
Given the mass kg m = (5 ± 0.5) kg and the velocity m/s v = ( 20 ± 0.4 ) m/s , we can find the kinetic energy and its uncertainty by applying the rules for the propagation of errors in multiplication.
For the product of two quantities, the relative error is the sum of the relative errors of the individual quantities:
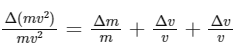
Now, substitute the given values:
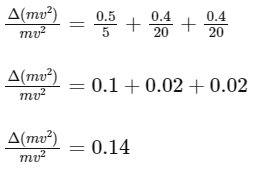
Now, calculate the kinetic energy:

To find the uncertainty in the kinetic energy, multiply the relative error by the calculated kinetic energy:
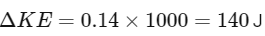
So, the kinetic energy of the body is (1000 ± 140)J.
Q4: Match List I with List II
 Choose the correct answer from the options given below:
Choose the correct answer from the options given below:
(a) A-IV, B-I, C-III, D-II
(b) A-II, B-III, C-I, D-IV
(c) A-II, B-I, C-IV, D-III
(d) A-I, B-III, C-II, D-IV
Ans: (c)
Let's analyze each item in List I and find the corresponding dimensional formula in List II.
A. Spring constant (k)
The spring constant is related to Hooke's Law, which states that the force exerted by a spring is proportional to its displacement: F = kx. The dimensional formula for force is [MLT − 2] , and for displacement is [L].
Dimensional formula of spring constant, k:
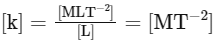
B. Angular speed (ω)
Angular speed is the rate of change of angular displacement with respect to time. The dimensional formula for angular displacement is the same as the plane angle, which is dimensionless. Therefore, the dimensional formula for angular speed is the reciprocal of the dimensional formula for time.
Dimensional formula of angular speed, ω:
[ω] = [T−1]
So, B matches with I.
C. Angular momentum (L)
Angular momentum is the product of the moment of inertia (I) and the angular velocity (ω). The dimensional formula for the moment of inertia is [ML2] , and the dimensional formula for angular velocity is [T−1] .
Dimensional formula of angular momentum, L:
[L] = [ML2] ⋅ [T−1] = [ML2 T−1]
So, C matches with IV.
D. Moment of inertia (I)
The moment of inertia is a measure of an object's resistance to rotational motion. It depends on the mass of the object and its distribution around the axis of rotation.
Dimensional formula of moment of inertia, I:
[I] = [ML2]
So, D matches with III.
The correct matching is A-II, B-I, C-IV, D-III
Q5: If force (F), velocity (V) and time (T) are considered as fundamental physical quantity, then dimensional formula of density will be :
(a) FV−2 T2
(b) FV4 T−6
(c) F2 V−2 T6
(d) FV−4 T−2
Ans: (d)
We know that force (F) has dimensions of MLT−2 , velocity (V) has dimensions of LT−1 , and time (T) has dimensions of T . To express density (ρ), which has dimensions of ML−3 , in terms of F, V, and T, we need to find the exponents of F, V, and T.
Let the dimensions of density be expressed as:
[M]a [L]b [T]c
Substituting the dimensions of F, V, and T:
[F]a [V]b [T]c = (MLT−2)a ( LT−1)b (T)c
Since density has dimensions of ML−3 , we can set up the following equations:
a = 1 (for the mass term M)
a + b = − 3 (for the length term L)
− 2a − b + c = 0 (for the time term T)
Solving these equations, we get:
a = 1
b = − 4
c = − 2
Thus, the dimensional formula of density in terms of F, V, and T is:
FV-4T-2
Q6: Given below are two statements:
Statements I: Astronomical unit (Au), Parsec (Pc) and Light year (ly) are units for measuring astronomical distances.
Statements II: Au < Parsec(Pc) < ly
In the light of the above statements, choose the most appropriate answer from the options given below:
(a) Both Statements I and Statements II are incorrect.
(b) Both Statements I and Statements II are correct,
(c) Statements I is incorrect but Statements II is correct.
(d) Statements I is correct but Statements II is incorrect.
Ans: (d)
Statement I is correct. Astronomical unit (AU), parsec (pc), and light year (ly) are indeed units for measuring astronomical distances.
However, Statement II is incorrect. The correct order of these units is:
AU < ly < Parsec (Pc)
1 AU is the average distance from the Earth to the Sun, which is about 93 million miles or 150 million kilometers.
1 light year is the distance that light travels in one year in a vacuum, which is approximately 9.461 trillion kilometers (5.878 trillion miles).
1 parsec is equal to about 3.26 light years, or approximately 30.9 trillion kilometers (19.2 trillion miles). Parsec (parallax of one arcsecond) is the distance at which an arc of length 1 Au subtends an angle of one arcsecond (1 Pc = 3.26 ly).
 So, the correct answer is Statement I is correct but Statement II is incorrect.
So, the correct answer is Statement I is correct but Statement II is incorrect.
Q7: In an experiment with vernier callipers of least count 0.1 mm , when two jaws are joined together the zero of vernier scale lies right to the zero of the main scale and 6th division of vernier scale coincides with the main scale division. While measuring the diameter of a spherical bob, the zero of vernier scale lies in between 3.2 cm and 3.3 cm marks, and 4th division of vernier scale coincides with the main scale division. The diameter of bob is measured as
(a) 3 .18 cm
(b) 3.22 cm
(c) 3.26 cm
(d) 3.25 cm
Ans: (a)
In this experiment, the vernier callipers have a least count of 0.1 mm, which is equal to 0.01 cm.
First, let's calculate the zero error since the zero of the vernier scale does not coincide with the zero of the main scale when the two jaws are joined together. The zero error can be found using the formula:
Zero Error = (Number of divisions coinciding) × Least Count
Zero Error = 6 × 0.01 cm = 0.06 cm
Since the zero of the vernier scale lies to the right of the main scale zero, the zero error is positive.
Now, let's find the main scale reading (MSR) when measuring the diameter of the spherical bob. The MSR is the value just before the zero of the vernier scale, which is 3.2 cm in this case.
Next, let's find the vernier scale reading (VSR) when measuring the diameter. The VSR is the product of the coinciding division number and the least count:
VSR = (Number of divisions coinciding) × Least Count
VSR = 4 × 0.01 cm = 0.04 cm
Now, we can find the total reading, which is the sum of the MSR and VSR:
Total Reading = MSR + VSR = 3.2 cm + 0.04 cm = 3.24 cm
Since there is a positive zero error, we need to subtract it from the total reading to get the corrected diameter:
Corrected Diameter = Total Reading - Zero Error = 3.24 cm - 0.06 cm = 3.18 cm
So, the diameter of the bob is measured as 3.18 cm.
Q8: A physical quantity P is given as
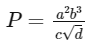
The percentage error in the measurement of a, b, c and d are 1%, 2%, 3% and 4% respectively. The percentage error in the measurement of quantity P will be
(a) 12%
(b) 13%
(c) 16%
(d) 14%
Ans: (b)
The percentage error in a quantity that is a product or quotient of other quantities is given by the sum of the percentage errors in those quantities, each multiplied by the power to which it is raised in the expression for the quantity.
Given the physical quantity P as
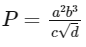
The percentage error in P, denoted as ΔP/P, is given by:

Substituting the given percentage errors for a, b, c, and d:

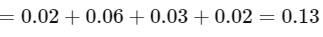
Therefore, the percentage error in P is 13%.
Q9: Match List I with List II
 Choose the correct answer from the options given below:
Choose the correct answer from the options given below:
(a) A-II, B-I, C-IV, D-III
(b) A-II, B-IV, C-I, D-III
(c) A-IV, B-II, C-III, D-I
(d) A-III, B-IV, C-I, D-II
Ans: (b)
Let's analyze the SI units of each quantity from List I:
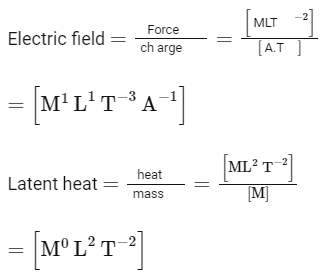
Torque: Torque (τ) is given by the cross product of the radius (r) and the force (F). Therefore, its SI units are Newton meter (Nm), which translates to ML2 T−2 in fundamental units.
Stress: Stress is force per unit area. The SI unit for force is the Newton (N) and for area is meter squared (m²). Therefore, the SI unit for stress is Pascal (Pa), which translates to ML−1 T−2 in fundamental units.
Pressure gradient: The pressure gradient is the rate of increase or decrease in pressure. It has units of pressure per distance. In SI units, that's Pascal per meter (Pa/m), which translates to ML − 2 T − 2 in fundamental units.
Coefficient of viscosity: This is a measure of a fluid's resistance to shear or flow, and its SI units are the Pascal second (Pa.s), which translates to ML−1 T−1 in fundamental units.
Therefore, the correct matches are:
A - II B - IV C - I D - III
Q10: Dimension of 1/ should be equal to
should be equal to
(a) T2/T2
(b) T/L
(c) L2/T2
(d) L/T
Ans: (c)
The term  appears in the formula for the speed of light c, which is:
appears in the formula for the speed of light c, which is:
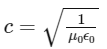
where μ0 is the permeability of free space and ∈0 is the permittivity of free space.
The speed of light c has dimensions of length over time (L/T). Therefore, the term  has dimensions equal to the square of the speed of light, which is L2/T2.
has dimensions equal to the square of the speed of light, which is L2/T2.
Q11: A cylindrical wire of mass (0.4 ± 0.01) g has length (8 ± 0.04) cm and radius (6 ± 0.03) mm. The maximum error in its density will be:
(a) 1%
(b) 5%
(c) 4%
(d) 3.5%
Ans: (c)
The density of a cylindrical wire is given by the formula:

where m is the mass, r is the radius, and l is the length.
The relative error in a calculated quantity is the sum of the relative errors in the quantities it depends on. For the density, this is given by:
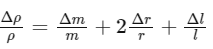
Given that Δ m = 0.01 g, m = 0.4 g, Δ r = 0.03 mm, r = 6 mm, Δl = 0.04 cm, and l = 8 cm, we can substitute these values into the formula to find the relative error in the density:
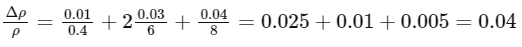
So the relative error in the density is 0.04, or 4%.
Q12: Two resistances are given as R1 = (10 ± 0.5) Ω and R2 = (15 ± 0.5) Ω. The percentage error in the measurement of equivalent resistance when they are connected in parallel is -
(a) 2.33
(b) 5.33
(c) 4.33
(d) 6.33
Ans: (c)
In the problem, we are given two resistances, R1 and R2 , each with a certain measurement error, Δ R1 and Δ R2. These resistances are connected in parallel, and we are asked to find the percentage error in the equivalent resistance of this combination.
The formula for the equivalent resistance R of two resistors R1 and R2 in parallel is:

We want to find the percentage error in R, which is given by (ΔR/R) × 100 % .
In order to find Δ R/R, we differentiate both sides of the above equation with respect to R , R1 , and R2. This gives us:

We can then solve this equation for ΔR/R:

Substituting the given values, R1 = 10 Ω , R2 = 15 Ω , Δ R1 = Δ R2 = 0.5 Ω , and R = R1 R2 / (R1 + R2) = 6 Ω , we get:
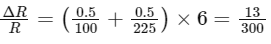
Finally, to convert this to a percentage, we multiply by 100, giving:
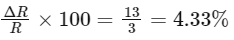
This tells us that the percentage error in the equivalent resistance of the two resistances in parallel is 4.33%.
Q13: If the velocity of light c , universal gravitational constant G and Planck's constant h are chosen as fundamental quantities. The dimensions of mass in the new system is :
(a) [ h1 c1 G−1]
(b) [h−1/2 c1/2 G1/2]
(c) [h1/2 c1/2 G−1/2]
(d) [h1/2c −1/2 G1]
Ans: (c)
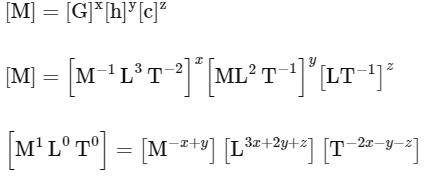
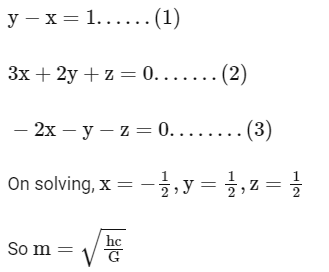
Q14: Match List I with List II
 Choose the correct answer from the options given below:
Choose the correct answer from the options given below:
(a) A - I, B - IV, C - III, D - II
(b) A - III, B - I, C - IV, D - II
(c) A - IV, B - II, C - I, D - III
(d) A - II, B - III, C - IV, D - I
Ans: (b)

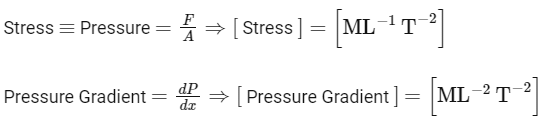
Q15: Match List I with List II:
 Choose the correct answer from the options given below:
Choose the correct answer from the options given below:
(a) A-IV, B-I, C-III, D-II
(b) A-IV, B-I, C-II, D-III
(c) A-I, B-IV, C-III, D-II
(d) A-IV, B-III, C-I, D-II
Ans: (a)
Torque → kg m2 s−2 (IV)
Energy density → kg m−1 s−2 (I)
Pressure gradient → kg m−2 s−2 (III)
Impulse → kg m s−1 (II)
Q16: The equation of a circle is given by x2 + y2 = a2, where a is the radius. If the equation is modified to change the origin other than (0, 0), then find out the correct dimensions of A and B in a new equation :  The dimensions of t is given as [T−1] .
The dimensions of t is given as [T−1] .
(a) A = [L−1 T−1] , B = [LT−1]
(b) A = [L−1 T−1] , B = [LT]
(c) A = [LT] , B = [L−1 T−1]
(d) A = [L−1 T] , B = [LT−1]
Ans: (c)
Here, At is distance, so dimensions of [ At] = [x] = [L]
Given. The dimensions of t is [T−1]
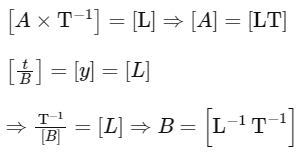
Q17: Match List I with List II:
 Choose the correct answer from the options given below:
Choose the correct answer from the options given below:
(a) A-III, B-II, C-IV, D-I
(b) A-III, B-II, C-I, D-IV
(c) A-II, B-III, C-IV, D-I
(d) A-II, B-III, C-I, D-IV
Ans: (a)
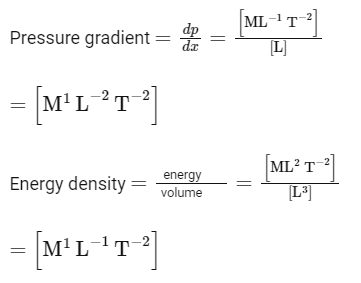
Q18: Match List I with List II
 Choose the correct answer from the options given below :
Choose the correct answer from the options given below :
(a) A-II, B-III, C-IV, D-I
(b) A-I, B-II, C-III, D-IV
(c) A-I, B-III, C-IV, D-II
(d) A-III, B-I, C-II, D-IV
Ans: (d)
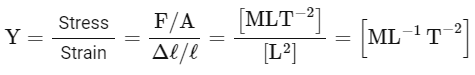
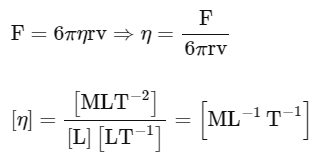
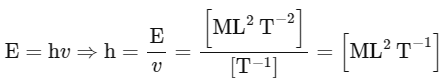
Work function has same dimension as that of energy, so [ϕ] = [ML2T-2]
Q19: Match List I with List II
 Choose the correct answer from the options given below:
Choose the correct answer from the options given below:
(a) A-I, B-III, C-IV, D-II
(b) A-III, B-IV, C-I, D-II
(c) A-II, B-IV, C-III, D-I
(d) A-III, B-I, C-II, D-IV
Ans: (b)
(A) Planck's constant
hv = E
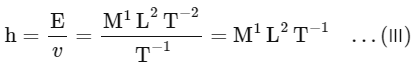
(B) E = qV
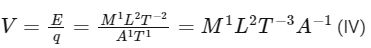
(C) ϕ ( work function ) = energy
= M1 L2 T−2 .... (I)
(D) Momentum (p) = F.t
= M1L1T-2T1
= M1L1T-1 ......(II)
[JEE Mains Numericals]
Q20: In a screw gauge, there are 100 divisions on the circular scale and the main scale moves by 0.5 mm on a complete rotation of the circular scale. The zero of circular scale lies 6 divisions below the line of graduation when two studs are brought in contact with each other. When a wire is placed between the studs, 4 linear scale divisions are clearly visible while th th th 46th division the circular scale coincide with the reference line. The diameter of the wire is ______________ × 10−2 mm.
Ans: 220

So diameter of wire = 2.23 mm − 0.03 mm
= 2.20 mm
= 220 × 10−2 mm
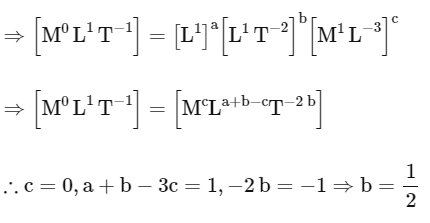
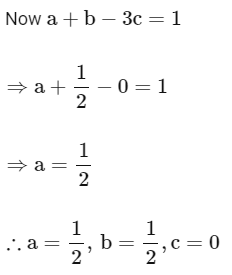
 is pressure, Y is volume, R is universal gas constant and T is temperature. The physical quantity equivalent to the ratio a/b is:
is pressure, Y is volume, R is universal gas constant and T is temperature. The physical quantity equivalent to the ratio a/b is: 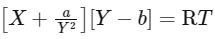
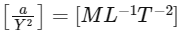

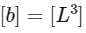
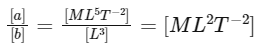
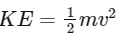
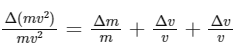
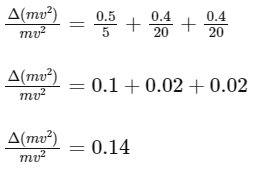

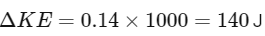
 Choose the correct answer from the options given below:
Choose the correct answer from the options given below: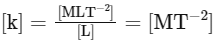
 So, the correct answer is Statement I is correct but Statement II is incorrect.
So, the correct answer is Statement I is correct but Statement II is incorrect.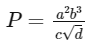
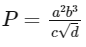


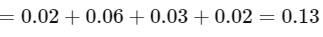
 Choose the correct answer from the options given below:
Choose the correct answer from the options given below: should be equal to
should be equal to appears in the formula for the speed of light c, which is:
appears in the formula for the speed of light c, which is: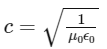
 has dimensions equal to the square of the speed of light, which is L2/T2.
has dimensions equal to the square of the speed of light, which is L2/T2.
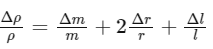
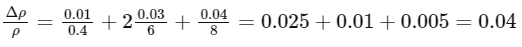



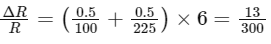
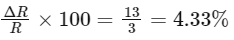
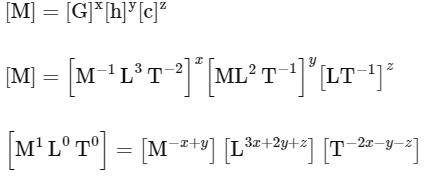
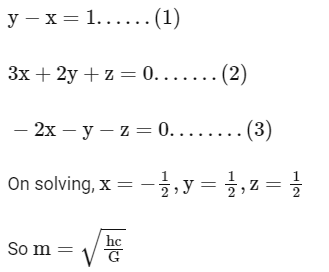
 Choose the correct answer from the options given below:
Choose the correct answer from the options given below:
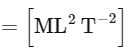
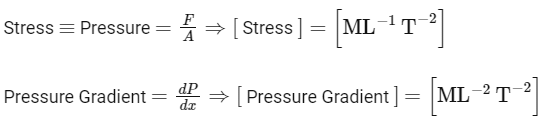
 Choose the correct answer from the options given below:
Choose the correct answer from the options given below: The dimensions of t is given as [T−1] .
The dimensions of t is given as [T−1] .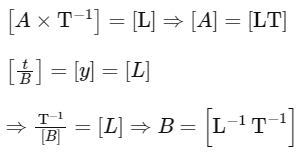
 Choose the correct answer from the options given below:
Choose the correct answer from the options given below: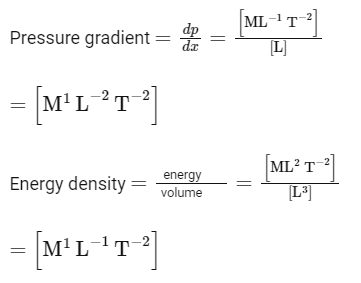

 Choose the correct answer from the options given below :
Choose the correct answer from the options given below :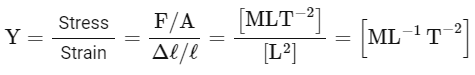
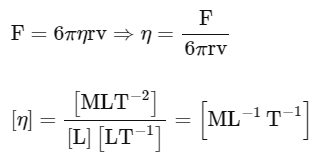
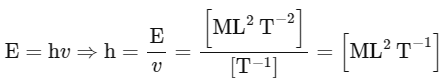
 Choose the correct answer from the options given below:
Choose the correct answer from the options given below: