Kepler's Laws of Planetary Motion | Physics for JEE Main & Advanced PDF Download
| Table of contents |

|
| Kepler's Laws of Planetary Motion |

|
| Kepler's First Law [The Law of Orbits] |

|
| Kepler's Second Law [The Law of Areas] |

|
| Kepler's Third law [The Law of Periods] |

|
Kepler's Laws of Planetary Motion
The motions of planet in universe have always been a puzzle. In 17th century Johannes Kepler, after a life time of study worded out some empirical laws based on the analysis of astronomical measurements of Tycho Brahe. Kepler formulated his laws, which are kinematical description of planetary motion. Now we discuss these laws step by step.
Kepler's First Law [The Law of Orbits]
Kepler's first law is illustrated in the image shown in figure. It states that "All the planets move around the sun in ellipitcal orbits with sun at one of the focus not at centre of orbit."
It is observed that the orbits of planets around sun are very less ecentric or approximately circular
Kepler's Second Law [The Law of Areas]
,epler's second Law is basically an alternative statement of law of conservation of momentum. It is illustrated in the image shown in figure(a). We know from angular momentum conservation, in elliptical orbit plane will move faster when it is nearer to the sun. Thus when a planet executes elliptical orbit its angular speed changes continuously as it moves in the orbit. The point of nearest approach of the planet to the sun is termed perihelion. The point of greatest seperation is termed aphelion. Hence by angular momentum conservation we can state that the planet moves with maximum speed when it is near perihelion and moves with slowest speed when it is near aphelion.
Kepler's second law states that "The line joining the sun and planet sweeps out equal areas in equal time or the rate of sweeping area by the position vector of the planet with respect to sun remains constant. "This is shown in figure (b).
The above statement of Kepler's second law can be verified by the law of conservation of angular momentum. To verify this consider the moving planet around the sun at a general point C in the orbit at speed v. Let at this instant the distance of planet from sun is r. If q be the angle between position vector of planet and its velocity vector then the angular momentum of planet at this instant is
L = mvr sinθ ...(1)
In an elemental time the planet will cover a small distance CD = dl and will travel to another adjacent point D as shown in figure (a), thus the distance CD = vdt. In this duration dt, the position vector sweeps out an area equal to that of triangle SCD, which is calculated as
Area of triangle SCD is dA = × r × vdt sin (π-θ)
= r v sinθ. dt
Thus the rate of sweeping area by the position vector is
Now from equation (1)
...(2)
The expression in equation (2) verifies the statement of Kepler' II law of planetary motion.
Kepler's Third law [The Law of Periods]
Kepler's Third Law is concerned with the time period of revolution of planets. It states that "The time period of revolution of a planet in its orbit around the sun is directly proportional to the cube of semi-major axis of the elliptical path around the sun"
If 'T' is the period of revolution and 'a' be the semi-major axis of the path of planet then according to Kepler's III law, we have
T2 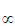 µ a3
µ a3
For circular orbits, it is a special case of ellipse when its major and minor axis are equal. If a planet is in a circular orbit of radius r around the sun then its revolution speed must be given as
Where Ms is the mass of sun. Here you can recall that this speed is independent from the mass of planet. Here the time period of revolution can be given as
or
Squaring equation written above, we get
...(1)
Equation (1) verifies the statement of Kepler's third law for circular orbits. Similarly we can also verify it for elliptical orbits. For this we start from the relation we've derived earlier for rate of sweeping area by the position vector of planet with respect to sun which is given as
Ex. The moon revolves around the earth 13 times per year. If the ratio of the distance of the earth from the sun to the distance of the moon from the earth is 392, find the ratio of mass of the sun to the mass of the earth.
Sol. The time period Te of earth around sun of mass Ms is given by
...(1)
Where re is the radius of the earth.
Similarly, time period Tm of moon around earth is given by
...(2)
Dividing equation(1) by equation (2), we get
or ...(3)
Substituting the given values, we get
Ex. A satellite revolves around a planet in an elliptical orbit. Its maximum and minimum distances from the planet are 1.5 × 107 m and 0.5 × 107 m respectively. If the speed of the satellite at the farthest point be 5 × 103 m/s, calculate the speed at the nearest point.
Sol.
In case of elliptical orbit, the speed of satellite varies constantly as shown in figure. Thus according to the law of conservation of angular momentum, the satellite must move faster at a point of closest approach (Perigee) than at a farthest point (Appogee).
We know that
Hence, at the two points, L = m v1 r1 = m v2 r2
or
Substituting the given values, we get
⇒ v2 = 1.5 × 104 m/s
Ex. Imagine a light planet revolving around a very massive star in a circular orbit of radius r with a period of revolution T. On what power of r, will the square of time period depend if the gravitational force of attraction between the planet and the star is proportional to r-5/2.
Sol. As gravitation provides centripetal force
, i.e.,
So that T = or
so T2 µ r7/2
Ex. A satellite is revolving round the earth in a circular orbit of radius a with velocity v0. A particle is projected from the satellite in forward direction with relative velocity . Calculate, during subsequent motion of the particle its minimum and maximum distances from earth's centre.
The corresponding situation is shown in figure.
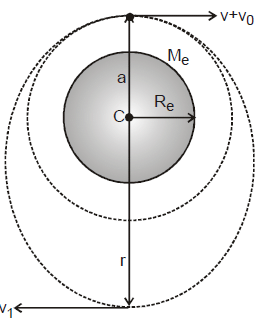
Initial velocity of satellite
When particle is thrown with the velocity v relative to satellite, the resultant velocity of particle will become
vR = v0+v
=
As the particle velocity is greater than the velocity required for circular orbit, hence the particle path deviates from circular path to elliptical path. At position of minimum and maximum distance velocity vectors are perpendicular to instantaneous radius vector. In this elliptical path the minimum distance of particle from earth's centre is a and maximum speed in the path is vR and let the maximum distance and minimum speed in the path is r and v1 respectively.
Now as angular momentum and total energy remain conserved. Applying the law of conservation of angular momentum, we have
m v1 r = m(v0 + v) a [m = mass of particle]
or =
Applying the law of conservation of energy
or
or 3r2 - 8 ar + 5 a2 = 0 or r = a or
Thus minimum distance of the particle = a
And maximum distance of the particle =
Ex. A sky lab of mass 2 × 103 kg is first launched from the surface of earth in a circular orbit of radius 2 R (from the centre of earth) and then it is shifted from this circular orbit to another circular orbit of radius 3 R. Calculate the minimum energy required (a) to place the lab in the first orbit (b) to shift the lab from first orbit to the second orbit. Given, R = 6400 km and g = 10 m/s2.
Sol. (a) The energy of the sky lab on the surface of earth
ES = KE + PE = 0 + =
And the total energy of the sky lab in an orbit of radius 2 R is
So the energy required to placed the lab from the surface of earth to the orbit of radius 2R is given as
E1 - Es =
or
or DE = (2 × 103 × 10 × 6.4 × 106) =
(12.8 × 1010) = 9.6 × 1010 J
(b) As for II orbit of radius 3R the total energy of sky lab is
or E2 - E1 =
or DE = =
= 1.1 × 1010 J
Ex. A satellite is revolving around a planet of mass M in an elliptic orbit of semi-major axis a. Show that the orbital speed of the satellite when it is at a distance r from the focus will be given by :
Sol. As in case of elliptic orbit with semi major axes a, of a satellite total mechanical energy remains constant, at any position of satellite in the orbit, given as
or KE PE = ...(1)
Now, if at position r, v is the orbital speed of satellite, we have
KE = and PE =
...(2)
So from equation (1) and (2), we have
=
, i.e.,
|
268 videos|740 docs|171 tests
|
FAQs on Kepler's Laws of Planetary Motion - Physics for JEE Main & Advanced
| 1. What are Kepler's Laws of Planetary Motion? |  |
| 2. What is Kepler's First Law? |  |
| 3. What is Kepler's Second Law? |  |
| 4. What is Kepler's Third Law? |  |
| 5. How do Kepler's Laws of Planetary Motion contribute to our understanding of the motion of planets in our solar system? |  |















