Class 10 Exam > Class 10 Notes > Lab Manuals for Class 10 > Lab Manual: Arithmetic Progression I
Lab Manual: Arithmetic Progression I | Lab Manuals for Class 10 PDF Download
Objective
To verify that the given sequence is an arithmetic progression by paper cutting and pasting method.Arithmetic Progression
A sequence is known as an arithmetic progression (sequence) if the difference between the term and its predecessor always remains constant.
Prerequisite Knowledge
Understanding the concept of an arithmetic progression.
Materials Required
Coloured papers, a pair of scissors, fevicol, geometry box, sketch pens, drawing sheets.
Procedure
- Take a given sequence of numbers say A1, A2, A,…
- Cut a rectangular strip from coloured paper of width 1 cm and length A, cm.
- Repeat the procedure by cutting rectangular strips of same width 1 cm and lengths A,, A3…cm.
- Take a graph paper and paste these rectangular strips adjacent to each other in order on graph paper.
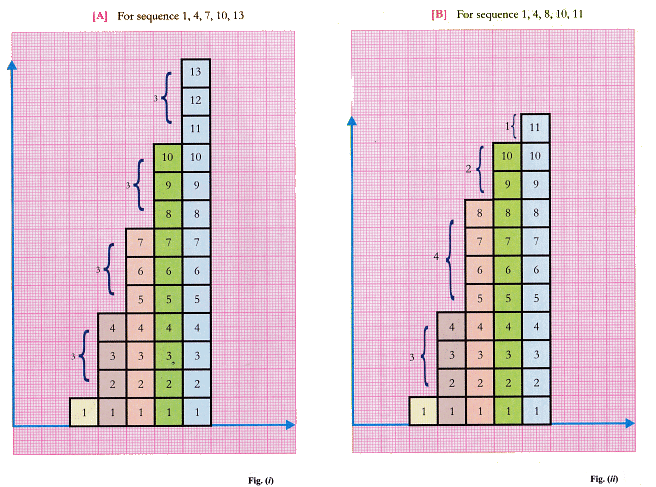
(A) Consider a sequence 1, 4, 7, 10, 13.
- Take different colour strips of lengths 1 cm, 4 cm, 7 cm, 10 cm, 13 cm and all of the same width 1 cm (say).
- Arrange and paste these strips in order on a graph paper as shown in fig. (i).
(B) Consider a sequence 1, 4, 8, 10, 11.
- Take different colour strips of lengths 1 cm, 4 cm, 8 cm, 10 cm, 11 cm and all of the same width 1 cm (say).
- Arrange and paste these strips in order on a graph paper as shown in fig. (ii).
Observation
We observe from fig(i) that the adjoining strips have a common difference in heights i.e. 3 cm and a ladder is formed in which the adjoining steps are constant. Hence it is an arithmetic progression. In fig (ii) the adjoining strips don’t have a common difference in heights and thus the adjoining steps of ladder are not constant. Hence it is not an arithmetic progression.
Learning Outcome
Students will learn the meaning of an arithmetic progression by relating it to an activity that involves visualisation.
Activity Time
Verify experimentally whether the following sequences are AP or not.
(i) 2, 4, 6, 8, 10
(ii) 3, 5, 6, 7, 11
(iii) 1, 5, 9, 13, 17
(iv)4, 7, 9, 10, 12
The document Lab Manual: Arithmetic Progression I | Lab Manuals for Class 10 is a part of the Class 10 Course Lab Manuals for Class 10.
All you need of Class 10 at this link: Class 10
FAQs on Lab Manual: Arithmetic Progression I - Lab Manuals for Class 10
| 1. What is an arithmetic progression? |  |
Ans. An arithmetic progression is a sequence of numbers in which the difference between any two consecutive terms is constant. For example, 2, 5, 8, 11, 14 is an arithmetic progression with a common difference of 3.
| 2. How can I find the nth term of an arithmetic progression? | |
Ans. To find the nth term of an arithmetic progression, you can use the formula: nth term = first term + (n-1) * common difference. Simply substitute the values of the first term, common difference, and the value of n into the formula to calculate the nth term.
| 3. What is the sum of an arithmetic progression? | |
Ans. The sum of an arithmetic progression can be calculated using the formula: sum = (n/2) * (first term + last term), where n is the number of terms in the progression. This formula sums up all the terms in the arithmetic progression.
| 4. How can I determine if a given sequence is an arithmetic progression? | |
Ans. To determine if a given sequence is an arithmetic progression, check if the difference between any two consecutive terms is the same. If the difference remains constant throughout the sequence, then it is an arithmetic progression.
| 5. Can an arithmetic progression have negative terms? | |
Ans. Yes, an arithmetic progression can have negative terms. The common difference, which is the difference between any two consecutive terms, can be positive, negative, or zero. So, an arithmetic progression can have a mix of positive and negative terms.
Related Exams
About this Document
|
4.64/5 Rating |
|
Dec 22, 2024 Last updated |
Document Description: Lab Manual: Arithmetic Progression I for Class 10 2024 is part of Lab Manuals for Class 10 preparation.
The notes and questions for Lab Manual: Arithmetic Progression I have been prepared according to the Class 10 exam syllabus. Information about Lab Manual: Arithmetic Progression I covers topics
like and Lab Manual: Arithmetic Progression I Example, for Class 10 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Lab Manual: Arithmetic Progression I.
Introduction of Lab Manual: Arithmetic Progression I in English is available as part of our Lab Manuals for Class 10
for Class 10 & Lab Manual: Arithmetic Progression I in Hindi for Lab Manuals for Class 10 course.
Download more important topics related with notes, lectures and mock test series for Class 10
Exam by signing up for free. Class 10: Lab Manual: Arithmetic Progression I | Lab Manuals for Class 10
Description
Full syllabus notes, lecture & questions for Lab Manual: Arithmetic Progression I | Lab Manuals for Class 10 - Class 10 | Plus excerises question with solution to help you revise complete syllabus for Lab Manuals for Class 10 | Best notes, free PDF download
Information about Lab Manual: Arithmetic Progression I
In this doc you can find the meaning of Lab Manual: Arithmetic Progression I defined & explained in the simplest way possible. Besides explaining types of
Lab Manual: Arithmetic Progression I theory, EduRev gives you an ample number of questions to practice Lab Manual: Arithmetic Progression I tests, examples and also practice Class 10
tests
|
Explore Courses for Class 10 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Sample Paper
,mock tests for examination
,Previous Year Questions with Solutions
,Exam
,Free
,shortcuts and tricks
,Lab Manual: Arithmetic Progression I | Lab Manuals for Class 10
,study material
,Viva Questions
,past year papers
,Semester Notes
,practice quizzes
,ppt
,Lab Manual: Arithmetic Progression I | Lab Manuals for Class 10
,Summary
,Lab Manual: Arithmetic Progression I | Lab Manuals for Class 10
,Objective type Questions
,video lectures
,MCQs
,Important questions
,Extra Questions
;
Additional Information about Lab Manual: Arithmetic Progression I for Class 10 Preparation
Lab Manual: Arithmetic Progression I Free PDF Download
The Lab Manual: Arithmetic Progression I is an invaluable resource that delves deep into the core of the Class 10 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Lab Manual: Arithmetic Progression I now and kickstart your journey towards success in the Class 10 exam.
Importance of Lab Manual: Arithmetic Progression I
The importance of Lab Manual: Arithmetic Progression I cannot be overstated, especially for Class 10 aspirants.
This document holds the key to success in the Class 10 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Lab Manual: Arithmetic Progression I Notes
Lab Manual: Arithmetic Progression I Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Lab Manual: Arithmetic Progression I.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Lab Manual: Arithmetic Progression I Notes on EduRev are your ultimate resource for success.
Lab Manual: Arithmetic Progression I Class 10 Questions
The "Lab Manual: Arithmetic Progression I Class 10 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 10 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Lab Manual: Arithmetic Progression I on the App
Students of Class 10 can study Lab Manual: Arithmetic Progression I alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Lab Manual: Arithmetic Progression I,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Lab Manual: Arithmetic Progression I is prepared as per the latest Class 10 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup