Lab Manual: Linear Equations - Class 10 PDF Download
Objective
To verify the conditions for consistency of a system of linear equations in two variables by graphical representation.
Linear Equation
An equation of the form ax + by + c = 0, where a, b, c are real numbers, a ≠ 0, b ≠ 0 and x, y are variables; is called a linear equation in two variables.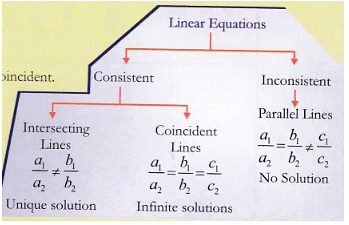
Prerequisite Knowledge
- Plotting of points on a graph paper.
- Condition of consistency of lines parallel, intersecting, coincident,
Materials Required
Graph papers, fevicol, geometry box, cardboard.
Procedure
Consider the three pairs of linear equations
- 1stpair: 2x-5y+4=0, 2x+y-8 = 0
- 2nd pair: 4x + 6y = 24, 2x + 3y =6
- 3rd pair: x-2y=5, 3x-6y=15
(a) Take the 1st pair of linear equations in two variables, e.g., 2x – 5y +4=0, 2x +y-8 = 0.
(b) Obtain a table of at least three such pairs (x, y) which satisfy the given equations. (c) Plot the points of two equations on the graph paper as shown.
(c) Plot the points of two equations on the graph paper as shown.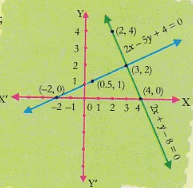 (d) Observe whether the lines are intersecting, parallel or coincident. Write the values in observation table. Also, check; (a1/a2); (b1/b2); (c1/c2)
(d) Observe whether the lines are intersecting, parallel or coincident. Write the values in observation table. Also, check; (a1/a2); (b1/b2); (c1/c2)
(e) Take the second pair of linear equations in two variables (f) Repeat the steps 3 and 4.
(f) Repeat the steps 3 and 4.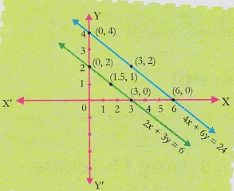 (g) Take the third pair of linear equations in two variables, i.e. x-2y=5, 3x-6y=15
(g) Take the third pair of linear equations in two variables, i.e. x-2y=5, 3x-6y=15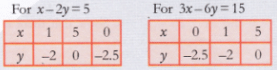 (h) Repeat steps 3 and 4
(h) Repeat steps 3 and 4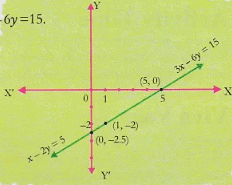
Obtain the condition for two lines to be intersecting, parallel or coincident from the observation table by comparing the values of (a1/a2), (b1/b2) and (c1/c2)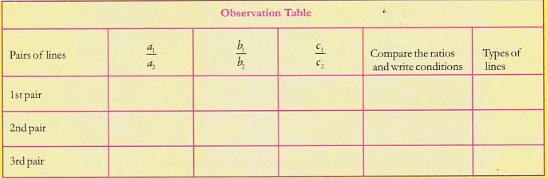
Observation
Students will observe that
- for intersecting lines, (a1/a2)≠(b1/b2)
- for parallel lines, (a1/a2)=(b1/b2)≠(c1/c2)
- for coincident lines, (a1/a2)=(b1/b2)=(c1/c2)
Result
The conditions for consistency of a system of linear equations in two variables is verified.
Learning Outcome
Students will learn that some pairs of linear equations in two variables have a unique solution (intersecting lines), some have infinitely many solutions (coincident lines) and some have no solutions (parallel lines).
Activity Time
Perform the same activity by drawing graphs of x-y+1=0 and 3x + 2y – 12 =0. Show that there is a unique solution. Also from the graph, calculate the area bounded by these linear equations and x-axis.
FAQs on Lab Manual: Linear Equations - Class 10
| 1. What are linear equations? |  |
| 2. How do you solve linear equations? |  |
| 3. Are there different methods to solve linear equations? |  |
| 4. Can linear equations have more than one solution? |  |
| 5. What are the applications of linear equations in real life? |  |





















