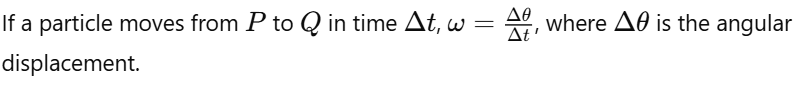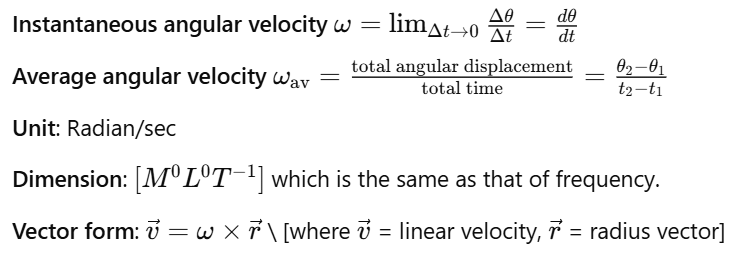Linear Momentum and Angular Momentum | Physics Class 11 - NEET PDF Download
| Table of contents |

|
| Angular Displacement |

|
| Angular Velocity |

|
| Angular Acceleration |

|
| Linear Momentum |

|
| Angular Momentum |

|
| Conservation of Angular Momentum |

|
| Equilibrium of a Rigid Body |

|
| Principle of moments |

|
Angular Displacement
It is the angle described by the position vector
about the axis of rotation.
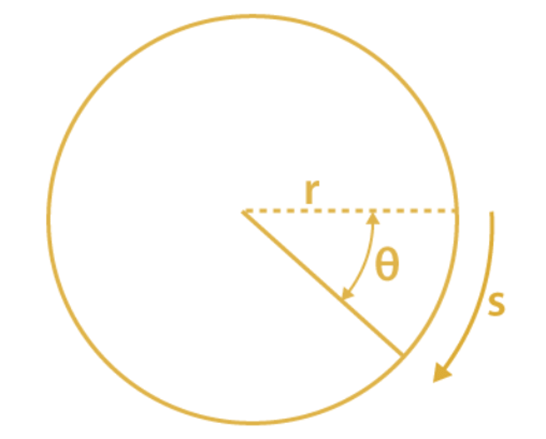 Angular Displacement
Angular Displacement
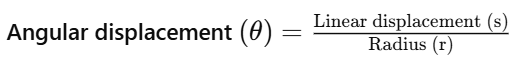

i.e., angular displacement is a vector quantity whose direction is given by the right-hand rule. It is also known as an axial vector. For anti-clockwise rotation, the direction of θ is perpendicular to the plane, outward along the axis of rotation, and vice-versa.

If a body rotates about a fixed axis then all the particles will have same angular displacement ( although linear displacement will differ from particle to particle in accordance with the distance of particles from the axis of rotation).
Angular Velocity
The angular displacement per unit time is defined as angular velocity.
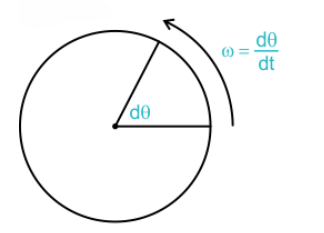 Angular Velocity
Angular Velocity
ω is an axial vector, whose direction is normal to the rotational plane and its direction is given by the right-hand screw rule.
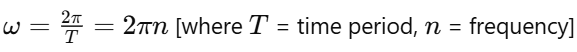
- The magnitude of an angular velocity is called the angular speed, which is also represented by
Angular Acceleration
The rate of change of angular velocity is defined as angular acceleration.
If a particle has angular velocity ω1 at time t1 and angular velocity ω2 at time t2, then:


It is an axial vector whose direction is along the change in direction of angular velocity, normal to the rotational plane, outward or inward along the axis of rotation (depending upon the sense of rotation).
Equations of Linear Motion and Rotational Motion

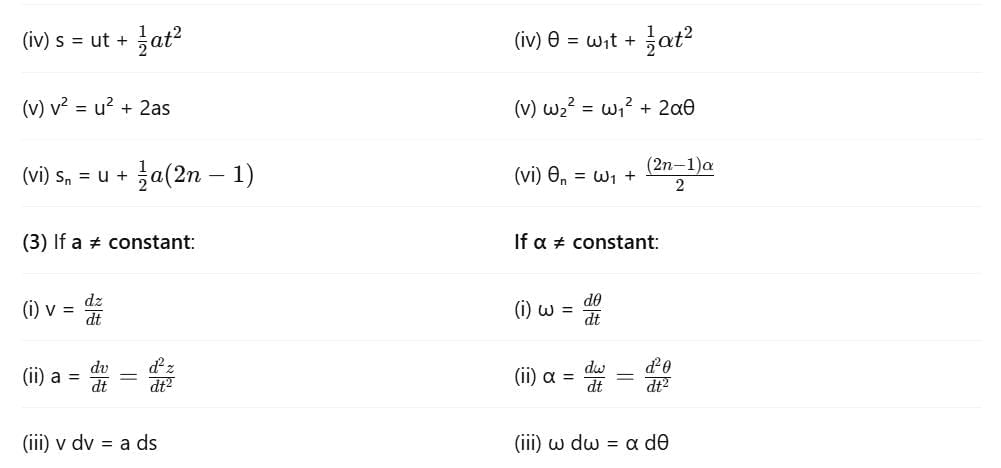
Linear Momentum
Linear momentum is a product of the mass (m) of an object and the velocity (v) of the object. If an object has higher momentum, then it harder to stop it.
The formula for linear momentum is p = mv.
The overall amount of momentum stays the same. This idea is known as the conservation of momentum.
Linear Momentum of a System of Particles
We know that the linear momentum of the particle is
p = mv
Newton’s second law for a single particle is given by,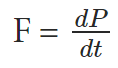
where F is the force of the particle. For ‘ n ‘ no. of particles, the total linear momentum is,
P = p1 + p2 +…..+pn
each of momentum is written as m1 v1 + m2v2 + ………..+ mnvn. We know that the velocity of the centre of mass is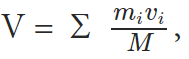
mv = Σ mivi
So comparing these equations, we get,
P = M V
Therefore, we can say that the total linear momentum of a system of particles is equal to the product of the total mass of the system and the velocity of its center of mass. Differentiating the above equation, we get,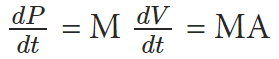
dv/dt is the acceleration of the centre of mass, and MA is the external force. So,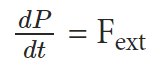
The above equation is nothing but Newton’s second law applied to a system of particles. If the total external force acting on the system is zero,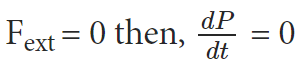
This means that P = constant. So whenever the total force acting on the system of a particle is equal to zero, then the total linear momentum of the system is constant or conserved. This is nothing but the law of conservation of total linear momentum of a system of particles.
Conservation of Total Linear Momentum of a System of Particles
- Radioactive Decay is a process where an unstable nucleus splits up into relatively stable nuclei, releasing a huge amount of energy.
- Suppose there is a parent nucleus which is unstable and it wants to become stable, to attain stability it will emit α particle and another daughter nucleus.
- This daughter nucleus is much more stable than the parent nucleus. This what radioactive decay is. Now suppose the parent nucleus is at rest and also the mass of the α is m and the daughter nucleus is M.
- So the mass of the parent nucleus will be m + M. Here everything that is happening is not due to the external force but all that happens is due to the internal force. So here Fext = 0, we can say that.
- We know the concept of torque as a turning effect of force. Torque is regarded as a rotational analog of force.
- According to Newton's second law of motion, force is equal to the rate of change of linear momentum.
- Therefore, if we can represent torque as the rate of change of some quantity, that quantity would be the rotational analog of linear momentum, and it can be called angular momentum, which we will study in detail in this document.
Angular Momentum
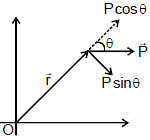
If p is the linear momentum of a particle in a given reference frame, then the angular momentum of the particle about an origin O in this reference frame is defined as
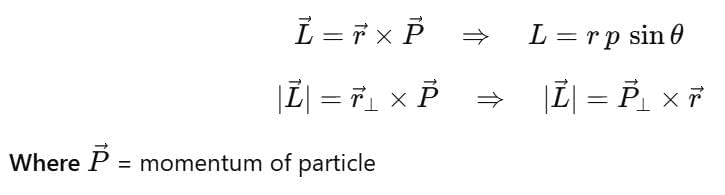
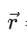 position vector of the particle with respect to the point about which angular momentum is to be calculated.
position vector of the particle with respect to the point about which angular momentum is to be calculated.
θ : angle between vectors r and p
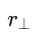 : perpendicular distance of the line of motion of particle from point O.
: perpendicular distance of the line of motion of particle from point O.
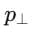 = perpendicular component of momentum.
= perpendicular component of momentum.
SI unit of angular momentum is kg m2 s-1.
Examples of Angular Momentum
- The angular velocity of a planet around the Sun increases when it comes near the Sun. When a planet revolving around the Sun in an elliptical orbit comes near the Sun, the moment of inertia of the planet about the Sun decreases. In order to conserve angular momentum, the angular velocity shall increase. Similarly, when the planet is away from the Sun, there will be a decrease in the angular velocity.
- The ice skater and the ballet dancer increase or decrease the angular velocity of spin about a vertical axis by pulling or extending out their limbs.

- A : axis is horizontal; angular momentum about vertical axis = 0.
B : axis is vertical; angular momentum about vertical axis is still zero; man and chair spin in direction opposite to spin of the wheel.
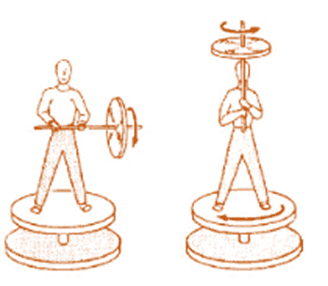
Torque or Moment of Force
When a body that is hinged, suspended, or pivoted starts to rotate due to the action of a force, the force is said to exert a torque on the body.
Torque, or the moment of force around a rotational axis, is determined by multiplying the force with the perpendicular distance from the axis of rotation to the line of action of the force.
The formula for calculating the magnitude of torque is:
Where b = r sinθ is called the lever arm or moment arm.
Units:
- In the M.K.S. system: Newton-meter (N·m)
- In the C.G.S. system: dyne-centimeter (dyne·cm)
Dimension: 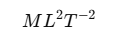
Vector form: 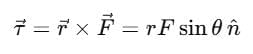

Torque is classified as an axial vector, meaning its direction is always perpendicular to the plane containing 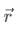 and
and 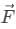 , and follows the right-hand rule.
, and follows the right-hand rule.
Relation between Torque and Angular Momentum
As we know that,
Differentiating with respect to the time we get,
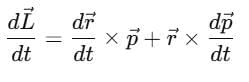
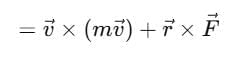
= 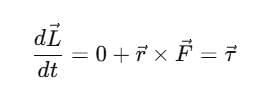 (
(  )
)
Couple
A couple refers to a specific combination of forces that can cause a body to rotate even when it is free to move. This is known as a couple of forces.
- A couple is defined as a pair of equal but opposite forces that do not act along the same line. The effect of a couple is measured by its moment of couple, or torque, which can be expressed as:
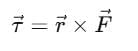

- Both torque and couple generally represent the same concept. However, the key difference lies in how the forces act: in a couple, both forces are applied externally, whereas, in torque, one force is external while the other is a reactionary force.
- The work done by torque when twisting a wire can be given as:
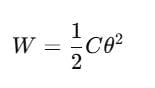
Where τ = Cθ, and C is referred to as the twisting coefficient or couple per unit twist.
Q1. A particle of mass m is moving along the line y = b, z = 0 with constant speed v. State whether the angular momentum of the particle about the origin is increasing, decreasing, or constant.
Sol:
constant as m, v, and b all are constants.
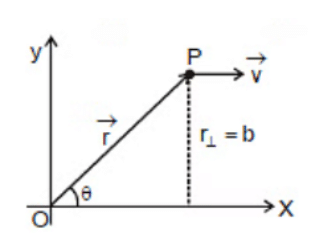
Direction of 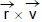 also remains the same. Therefore, the angular momentum of the particle about the origin remains constant with due course of time.
also remains the same. Therefore, the angular momentum of the particle about the origin remains constant with due course of time.
Note: In this problem is increasing, q is decreasing but r sin q, i.e., b remains constant. Hence, the angular momentum remains constant.
Q2. A particle of mass m is projected with velocity v at an angle q with the horizontal. Find its angular momentum about the point of projection when it is at the highest point of its trajectory.
Sol: At the highest point, it has only horizontal velocity vx = v cos q. The length of the perpendicular to the horizontal velocity from 'O' is the maximum height, where
⇒ Angular momentum L =
Angular Momentum of a Rigid Body Rotating About a Fixed Axis
- Suppose a particle P of mass m is going in a circle of radius r and at some instant the speed of the particle is v.
- For finding the angular momentum of the particle about the axis of rotation, the origin may be chosen anywhere on the axis.
- We choose it at the center of the circle. In this case
 are perpendicular to each other
are perpendicular to each other 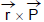 and are along the axis. Thus, the component along the axis is mvr itself.
and are along the axis. Thus, the component along the axis is mvr itself. - The angular momentum of the whole rigid body about AB is the sum of components of all particles, i.e., L =
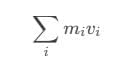
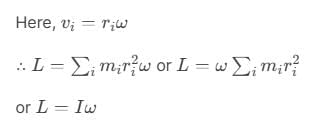
Here, I is the moment of inertia of the rigid body about AB.
Note: Angular momentum about the axis is the component of along the axis. In most of the cases, angular momentum about axis is Iω.
Q3. Two small balls A and B, each of mass m, are attached rigidly to the ends of a light rod of length d. The structure rotates about the perpendicular bisector of the rod at an angular speed w. Calculate the angular momentum of the individual balls and of the system about the axis of rotation.
Sol:
Consider the situation shown in the figure. The velocity of the ball A with respect to the center O is
v = .
The angular momentum of the ball with respect to the axis is
L1 = mvr = =
mwd2. The same is the angular momentum L2 of the second ball. The angular momentum of the system is equal to the sum of these two angular momenta i.e., L = 1/2 mwd2.
Conservation of Angular Momentum
- The time rate of change of angular momentum of a particle about some reference point in an inertial frame of reference is equal to the net torques acting on it.
- Now, suppose that,
 then,
then, 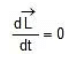 so that
so that 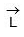 = constant.
= constant. - When the resultant external torque acting on a system is zero, the total vector angular momentum of the system remains constant. This is the principle of the conservation of angular momentum.
- For a rigid body rotating about an axis (the z-axis, say) that is fixed in an inertial reference frame, we have Lz = I w
- It is possible for the moment of inertia I of a rotating body to change by rearrangement of its parts. If no net external torque acts, then L z must remain constant and if I do change, there must be a compensating change in w. The principle of conservation of angular momentum in this case is expressed. Iw = constant
Q4. A wheel of the moment of inertia I and radius R is rotating about its axis at an angular speed of w0. It picks up a stationary particle of mass m at its edge. Find the new angular speed of the wheel.
Sol: The net external torque on the system is zero. Therefore, angular momentum will remain conserved. Thus,
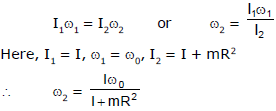
Note:
Comments on Linear Momentum :
Case I: Linear momentum is not conserved just before and just after collision because during collision hinge force acts as an external force.
Case II: Linear momentum is conserved just before and just after collision because no external force on the string.
Comments on Angular Momentum :
Case I: Hinge force acts at an external force during collision but except point A all the other reference points given  . So angular momentum is conserved only for point A.
. So angular momentum is conserved only for point A.
Case II: Angular momentum is conserved at all points in the world.
Q5. A uniform rod of mass m and length l can rotate freely on a smooth horizontal plane about a vertical axis hinged at point H. A point mass having the same mass m coming with an initial speed u perpendicular to the rod, strikes the rod in-elastically at its free end. Find out the angular velocity of the rod just after collision.
Sol:
Angular momentum is conserved about H because no external force is present in the horizontal plane which is producing torque about H.
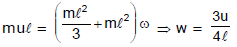
Q6. A uniform rod of mass m and length l can rotate freely on a smooth horizontal plane about a vertical axis hinged at point H. A point mass having the same mass m coming with an initial speed u perpendicular to the rod, strikes the rod and sticks to it at a distance of 3l/4 from the hinge point. Find out the angular velocity of the rod just after collision.
Sol:
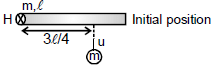
From angular momentum conservation about H, initial angular momentum = final angular momentum
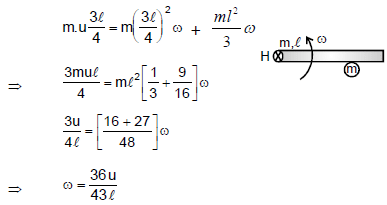
Q7. A uniform rod AB of mass m and length 5a is free to rotate on a smooth horizontal table about a pivot through P, a point on AB such that AP = a. A particle of mass 2m moving on the table strikes AB perpendicularly at the point 2a from P with speed v, the rod being at rest. If the coefficient of restitution between them is , find their speeds immediately after impact.
Sol:
Let the point of impact be Q so that
PQ = 2a
Let P be the point of pivot that AP = a
Let the velocities of point, Q, and the particle after impact be vq and vp respectively then from momentum conservation about point P.
Li = Lf
Equilibrium of a Rigid Body
We can say rigid body is in equilibrium when it is in
(a) Translational equilibrium
Fnet x = 0 and Fnet y = 0 and
(b) Rotational equilibrium
Note :
(i) If net force on the body is zero then net torque of the forces may or may not be zero.
Example:
(1) A pair of forces each of same magnitude and acting in opposite direction on the rod.
(2) If net force on the body is zero then torque of the forces about each and every point is same
t about B
t about C
Translatory and Rotatory Equilibrium
Q8. Determine the point of application of third force for which body is in equilibrium when forces of 20 N & 30 N are acting on the rod as shown in figure
Sol: Let the magnitude of third force is F, is applied in upward direction then the body is in the equilibrium when
(i) (Translational Equillibrium)
⇒ 20 + F = 30 ⇒ F = 10 N
So the body is in translational equilibrium when 10 N force act on it in upward direction.
(ii)Let us assume that this 10 N force act. Then keep the body in rotational equilibrium So Torque about C = 0
30 x 20 = 10 x
x = 60 cm
so 10 N force is applied at 70 cm from point A to keep the body in equilibrium.
Q9. Determine the point of application of force, when forces are acting on the rod as shown in figure.
Sol: Since the body is in equillibrium so we conclude and torque about any point is zero i.e.,
Let us assume that we apply F force downward at A angle q from the horizontal, at x distance from B
⇒ Fnet x = 0 which gives
F2 = 8 N
From Fnet y = 0 ⇒ 5 + 6 = F1 + 3
⇒ F1 = 8 N
If body is in equilibrium then torque about point B is zero,
⇒ 3 x 5 + F1 x - 5 x 10 = 0
⇒ 15 + 8x - 50 = 0
Q10. A uniform rod of length l, mass m is hung from two strings of equal length from a ceiling as shown in figure. Determine the tensions in the strings?
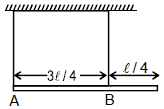
Sol: Let us assume that the tension in the left and right strings is TA and TB, respectively. Then
Rod is in equilibrium then
From
mg = TA + TB ...(1)
Q11. A stationary uniform rod of mass `m', length `l' leans against a smooth vertical wall, making an angle q with the rough horizontal floor. Find the normal force & frictional force that is exerted by the floor on the rod?
Sol: As the rod is stationary so the linear acceleration and angular acceleration of rod is zero.
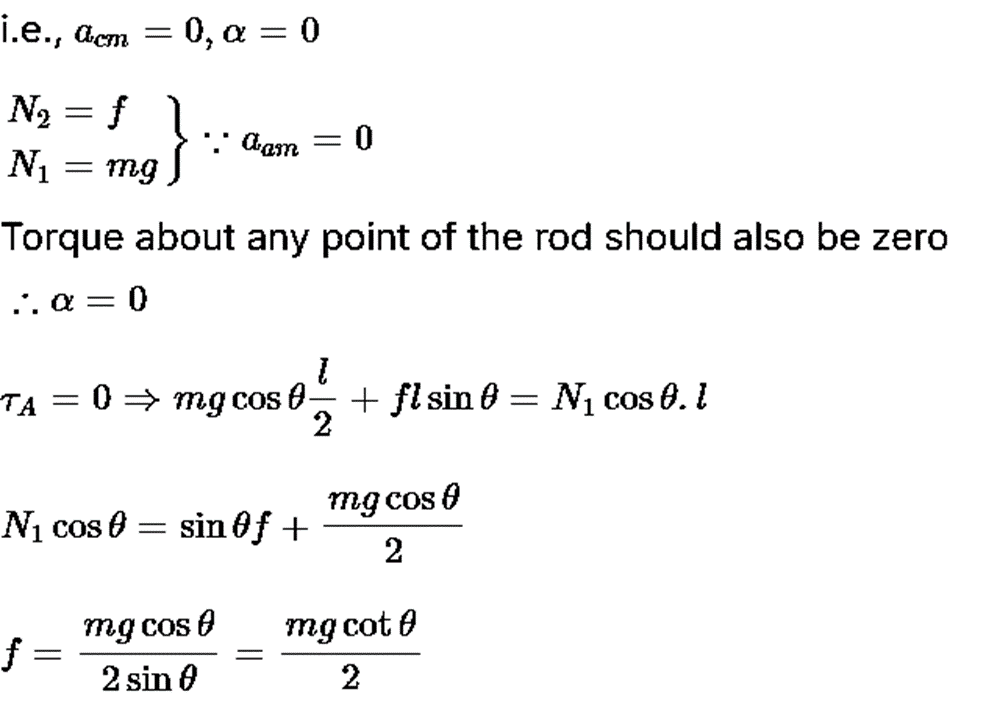
Principle of moments
Consider a light rod of negligible mass which is pivoted at a point along its length. Let two parallel forces F1 and F2 act at the two ends at distances d1 and d2 from the point of pivot and the normal reaction force N at the point of pivot as shown in figure. If the rod has to remain stationary in horizontal position, it should be in translational and rotational equilibrium. Then, both the net force and net torque must be zero.
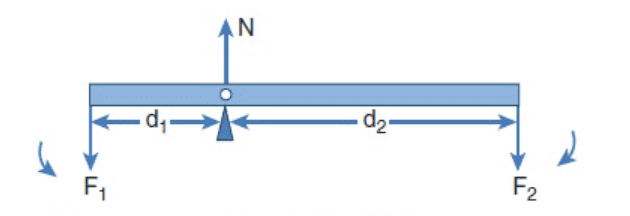
For net force to be zero, − F1 + N − F2 = 0
N = F1 + F2
For net torque to be zero, d1F1 − d2 F2 = 0
d1F1 = d2F2
The above equation represents the principle of moments. This forms the principle for beam balance used for weighing goods with the condition d1 = d2; F1 = F2. We can rewrite above equation as,
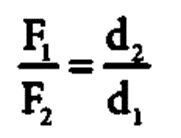
If F1 is the load and F2 is our effort, we get advantage when, d1< d2. This implies that F1> F2. Hence, we could lift a large load with small effort. The ratio (d2/d1) is called mechanical advantage of the simple lever. The pivoted point is called fulcrum.

There are many simple machines that work on the above mentioned principle.
|
96 videos|367 docs|98 tests
|
FAQs on Linear Momentum and Angular Momentum - Physics Class 11 - NEET
| 1. What is the difference between angular displacement and angular velocity? |  |
| 2. How is angular acceleration defined and what is its significance? |  |
| 3. What is the law of conservation of angular momentum? |  |
| 4. How does the principle of moments apply to the equilibrium of a rigid body? |  |
| 5. How are linear momentum and angular momentum related? |  |