Vector Product of Two Vectors | NCERT on your Fingertips 2025-2026 Edition - NEET PDF Download
The cross product, area product or the vector product of two vectors is a binary operation on two vectors in three-dimensional spaces. It is denoted by ×. The cross product of two vectors is a vector. Let us consider two vectors denoted as. Let the product (also a vector) of these two vectors be denoted as.
Magnitude of the vector product
The magnitude of the vector product is given as,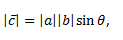
Where a and b are the magnitudes of the vector and Ɵ is the angle between these two vectors. From the figure, we can see that there are two angles between any two vectors, that is, Ɵ and (360° – Ɵ). In this rule, we always consider the smaller angle that is less than 180°.
Direction of the vector product
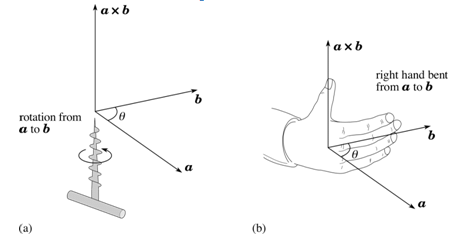
The right-hand thumb rule is used in which we curl up the fingers of right hand around a line perpendicular to the plane of the vectors a and b and the curl the fingers in the direction from a to b, then the stretched thumb points in the direction of c.
Commutative property
Unlike the scalar product, cross product of two vectors is not commutative in nature. Mathematically, for scalar products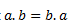
But for vector products
As we know, the magnitude of both the cross products a × b and b × a is the same and is given by absinθ; but the curling of the right-hand fingers in case of a × b is from a to b, whereas in case of (b × a) it is from b to a, as per which, the two vectors are in opposite directions.
Mathematically,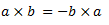
Distributive property
Like the scalar product, vector product of two vectors is also distributive with respect to vector addition. Mathematically,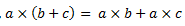
In order to deal with the vector product of any two vectors, we need to know the vector product of two elementary vectors.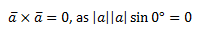
Similarly, for the unit vectors following results hold good,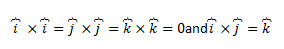
|
1083 docs|708 tests
|
FAQs on Vector Product of Two Vectors - NCERT on your Fingertips 2025-2026 Edition - NEET
| 1. What is the vector product of two vectors? |  |
| 2. How is the vector product calculated? |  |
| 3. What is the significance of the angle between the two vectors in the vector product? |  |
| 4. How can the direction of the vector product be determined? |  |
| 5. What are some applications of the vector product in physics and engineering? |  |





















