Theorems of Perpendicular & Parallel Axis | Physics for JEE Main & Advanced PDF Download
Before we study the theorems of parallel and perpendicular axis let us first see what moment of inertia is. Moment of inertia is the property of the body due to which it resists angular acceleration, which is the sum of the products of the mass of each particle in the body with the square of its distance from the axis of rotation.
∴ Moment of inertia I = Σ miri2
So in order to calculate the moment of inertia we use two important theorems which are the perpendicular and parallel axis theorem.
Perpendicular Axis Theorem
This theorem is applicable only to the planar bodies. Bodies which are flat with very less or negligible thickness. This theorem states that the moment of inertia of a planar body about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes concurrent with the perpendicular axis and lying in the plane of the body.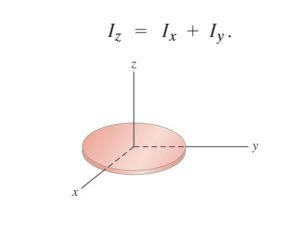
In the above figure, we can see the perpendicular body. So Z axis is the axis which is perpendicular to the plane of the body and the other two axes lie in the plane of the body. So this theorem states that
IZ = Ix + Iy
That means the moment of inertia about an axis which is perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes.
Let us see an example of this theorem:
Suppose we want to calculate the moment of inertia of a uniform ring about its diameter. Let its centre be MR²/2, where M is the mass and R is the radius. So, by the theorem of perpendicular axes, IZ = Ix + Iy. Since the ring is uniform, all the diameters are equal.
∴ Ix = Iy
∴ IZ = 2 Ix
Iz = MR²/4
So finally the moment of inertia of a disc about any of its diameter is MR²/4
Parallel Axis Theorem
Parallel axis theorem is applicable to bodies of any shape. The theorem of parallel axis states that the moment of inertia of a body about an axis parallel to an axis passing through the centre of mass is equal to the sum of the moment of inertia of body about an axis passing through centre of mass and product of mass and square of the distance between the two axes.
IZ’ = Iz + Mα²
where, α is the distance between two axes.
|
297 videos|953 docs|172 tests
|
















