JEE Advanced (Matrix Match & Integer Answer): Ray & Wave Optics | Chapter-wise Tests for JEE Main & Advanced PDF Download
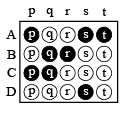
DIRECTIONS (Q. No. 1-4) : Each question contains statements given in two columns, which have to be matched. The statements in Column-I are labelled A, B, C and D, while the statements in ColumnII are labelled p, q, r and s. Any given statement in Column-I can have correct matching with ONE OR MORE statement(s) in Column-II. The appropriate bubbles corresponding to the answers to these questions have to be darkened as illustrated in the following example :
If the correct matches are A-p, s and t; B-q and r; C-p and q; and D-s then the correct darkening of bubbles will look like the given.
Q.1. A simple telescope used to view distant objects has eyepiece and objective lens of focal lengths fe and fo, respectively. Then (2006 - 6M)
| Column I | Column II |
| (A) Intensity of light received by lens | (p) Radius of aperture |
| (B) Angular magnification | (q) Dispersion of lens |
| (C) Length of telescope | (r) Focal length of objective lens and eyepiece lens |
| (D) Sharpness of image | (s) Spherical aberration |
Ans. A-p; B-r; C-r; D-p, q, s
Solution. (A) → (p).
More the radius of aperture more is the amount of light entering the telescope.
(B) → (q).
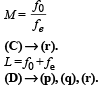
Depends on dispersion of lens, spherical aberration and radius of aperture.
Q.2. An optical component and an object S placed along its optic axis are given in Column I. The distance between the object and the component can be varied. The properties of images are given in Column II. Match all the properties of images from Column II with the appropriate components given in Column I. Indicate your answer by darkening the appropriate bubbles of the 4 × 4 matrix given in the ORS.
| Column I | Column II |
 | (p) real image |
 | (q) virtual image |
 | (r) magnified image |
 | (s) image at infinity |
Ans. A-p, q, r, s; B-q; C-p, q, r, s; D-p, q, r, s
Solution. A-p, q, r, s l
- When th e object is at in finity, a real, inver ted and diminished image is formed at the focus of the concave mirror.
- As the object is brought closer to the mirror, the image moves farther, remains real and inverted and increases in size (but still it is diminished as compared to the object) l When the object is at C, a real, inverted and same size image is formed at C.
- When the object is brought still closer, a real, inverted and magnified image is formed beyond C.
- When the object is at focus (F), the image is highly magnified, real and inverted and formed at infinity.
- When the object is placed between pole and focus, a virtual, erect and magnified image is formed behind the mirror.
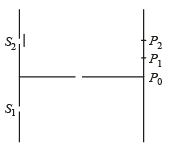
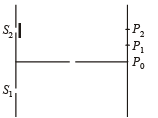
Q.3. Column-I shows four situations of standard Young’s double slit arrangement with the screen placed far away from the slits S1 and S2. In each of these cases S1P0 = S2P0, S1P1-S2P1 = λ/4 and S1P2– S2P2 = λ /3, where λ is the wavelength of the light used. In the cases B, C and D, a transparent sheet of refractive index μ and thickness t is pasted on slit S2. The thicknesses of the sheets are different in different cases. The phase difference between the light waves reaching a point P on the screen from the two slits is denoted by d (P) and the intensity by δ(P). Match each situation given in Column-I with the statetment(s) in Column-II valid for that situation.
| Column-I | Column-II |
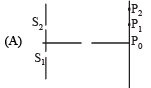 | (p) δ(P0) = 0 |
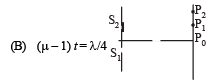 | (q) δ (P1) = 0 |
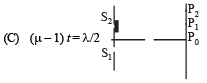 | (r) I (P1) = 0 |
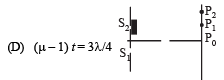 | (s) I(P0) > I (P1) |
| (t) I(P2) > I (P1) |
Ans. A-p, s; B-q; C-t; D-r, s, t
Solution.
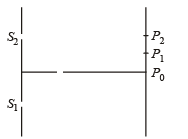
For path difference λ /4 , phase difference is π /2 .
For path difference λ/3 , phase difference is 2π /3 .
Here, S1P0 - S2P0 = 0
∴ δ (P0) = 0
Therefore, (p) matches with (A).
The path difference for P1 and P2 will not be zero. The intensities at P0 is maximum.
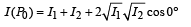

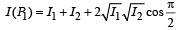
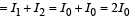
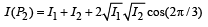
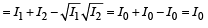
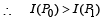
Therefore, (s) matches with (A).
(B)
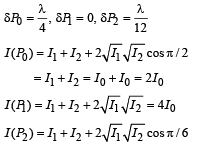
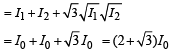
Therefore, q match with (B)
(C)
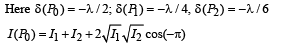
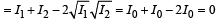
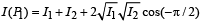
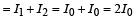
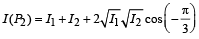
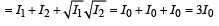
∴ I (P2) > I (P1)
(t) matches (C).
(D)
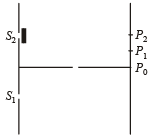
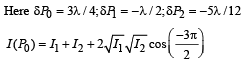
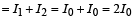
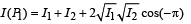
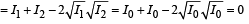
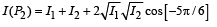
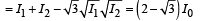
(r), (s), (t) matches (D).
Q.4. Two transparent media of refractive indices μ1 and μ3 have a solid lens shaped transparent material of refractive index μ2 between them as shown in figures in Column II. A ray traversing these media is also shown in the figures. In Column I different relationships between μ1, μ2, and μ3 are given. Match them to the ray diagrams shown in Column II. (2010)
| Column I | Column II |
| (A) μ1 < μ2 | 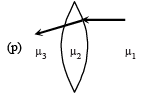 |
| (B) μ1 > μ2 |  |
| (C) μ2 = μ3 | 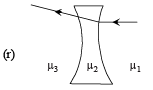 |
| (D) μ2 > μ3 | 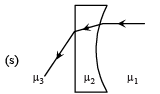 |
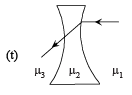 |
Ans. A-p, r; B-q, s, t; C-p, r, t; D-q, s
Solution. (a) When μ1 < μ2, the ray of light while entering the lens will bend towards the normal. Therefore p, r are the correct options
(B) When μ1> μ2, the ray of light while entering the lens will bend away from the normal. Therefore q,s,t are the correct options.
(C) When μ2 = μ3, the ray of light while coming out from the lens does not deviate from its path. Therefore p,r,t are the correct option.
(D) μ2> μ3, the ray of light coming out of the lens deviates away from the normal. Therefore q,s are the correct options.
DIRECTION (Q. No. 5 & 6) Following question has matching lists. The codes for the lists have choices (a), (b), (c) and (d) out of which ONLY ONE is correct.
Q.5. A right angled prism of refractive index μ1 is placed in a rectangular block of refractive index μ2, which is surrounded by a medium of refractive index μ3, as shown in the figure. A ray of light 'e' enters the rectangular block at normal incidence. Depending upon the relationships between μ1, μ2 and μ3, it takes one of the four possible paths 'ef', 'eg', 'eh' or 'ei'.
Match the paths in List I with conditions of refractive indices in List II and select the correct answer using the codes given below the lists: (JEE Adv. 2013)
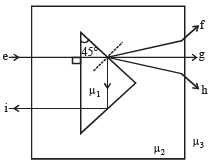
| List I | List II |
| P. e → f | 1. μ1 > 2μ2 |
| Q. e → g | 2. μ2 > μ1 and μ2 > μ3 |
| R. e → h | 3. μ1 = μ2 |
| S. e → i | 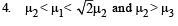 |
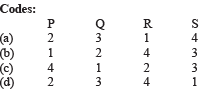
Ans. (d)
Solution. e → f. For the ray to bend towards the normal at the prism surface μ2 > μ1. The ray then moves away from the normal when it emerges out of the rectangular block. Therefore μ2 > μ3.
e → g. As there is no deviation of the ray as it emerges out of the prism, μ2 = μ1.
e → h. As the ray emerges out of prism, it moves away from the normal. Therefore μ2 < μ1. As the ray moves away from the normal as it emerges out of the rectangular block, therefore μ2 > μ3.
e → i. At the prism surface, total internal reflection has taken place. For this sin 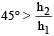
∴ m1 > √2 μ2. (d) is the correct option.
Q.6. Four combinations of two thin lenses are given in List-I. The radius of curvature of all curved surfaces is r and the refractive index of all the lenses is 1.5. Match lens combinations in List-I with their focal length in List-II and select the correct answer using the code given below the lists. (JEE Adv. 2014)
| List - I | List - II |
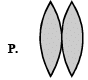 | 1. 2r |
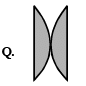 | 2. r/2 |
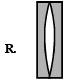 | 3. – r3. – r |
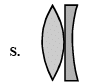 | 4. r |
Codes:
(a) P-1, Q-2, R-3, S-4
(b) P-2, Q-4, R-3, S-1
(c) P-4, Q-1, R-2, S-3
(d) P-2, Q-1, R-3, S-4
Ans. (b)
Solution. 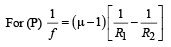
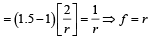
For the combination
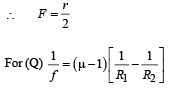
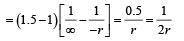
∴ f = 2r
For the combination
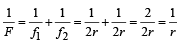
∴ f = r
Similarly, we can either find or do not find the remaining options (b) is the correct option.
|
446 docs|929 tests
|



















