Class 10 Mathematics: CBSE Sample Question Paper (2020-21) (Basic) - 3 | Mathematics (Maths) Class 10 PDF Download
Class X
Mathematics – Basic
Sample Question Paper 2020-21
Max. Marks : 80
Duration : 3 hrs.
General Instructions :
1. This question paper contains two parts A and B.
2. Both Part A and Part B have internal choices.
Part – A
1. It consists of two sections- I and II.
2. Section I has 16 question. Internal choice is provided in 5 questions.
3. Section II has four case study-based questions. Each case study has 5 case-based sub-parts. An examinee is to attempt any 4 out of 5 sub-parts.
Part – B
1. Question No 21 to 26 are Very short answer Type questions of 2 marks each.
2. Question No 27 to 33 are Short Answer Type questions of 3 marks each.
3. Question No 34 to 36 are Long Answer Type questions of 5 marks each.
4. Internal choice is provided in 2 questions of 2 marks, 2 questions of 3 marks and 1 question of 5 marks.
Part – A
Section - I
Q.1. Find the sum of the zeroes of the polynomial x2 – 3x + 1: (1 Mark)
Ans. Sum of zeroes = − (Coefficient of x) / (Coefficient of x2)
= -(-3) / 1 = 3
Q.2. If a pair of linear equations is inconsistent, then the lines will be. (1 Mark)
Ans. Condition for inconsistency:
a1 / a2 = b1 / b2 ≠ c1 / c2 has no solution (inconsistent), i.e., do not intersect at any point.
So the lines are parallel.
Q.3. In an A.P., if d = 6, n = 35, a = 3, find the value of a35. (1 Mark)
Ans. In the given A.P., d = 6, n = 35, a = 3
an = a + (n – 1) d
∴ a35 = 3 + (35 – 1) (6)
= 3 + 204
∴ a35 = 207.
Q.4. Find the distance between the points A (–2, –3) and B (– 4, 4). (1 Mark)
OR
In ΔABC, if X and Y are points on AB and AC respectively such that AX / XB = 3 / 4, AY = 5 and YC = 9, then state whether XY and BC parallel or not. (1 Mark)
Ans. By distance formula, distance between (x1, y1) and (x2, y2) is given by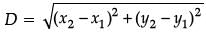
∴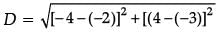
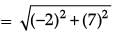
= √53.
OR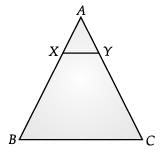 Given, AX / XB = 3 / 4, AY = 5 and YC = 9
Given, AX / XB = 3 / 4, AY = 5 and YC = 9
Then, AX / XB = 3 / 4 and AY / YC = 5 / 9
∴ AX / XB ≠ AY / YC
Hence XY is not parallel to BC.
Q.5. If the distance between the points (– 3, p) and (3, 5) is 3√5 , then find the value of p. (1 Mark)
Ans. By distance formula, distance between (x1, y1) and (x2, y2) is given by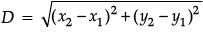
(x1, y1) = (–3, p) and (x2, y2) = (3, 5)
∴ 3√5 =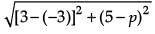
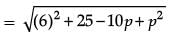
45 = 61 – 10p + p2
∴ p2 – 10p + 16 = 0
(p – 2) (p – 8) = 0
∴ p = 2 or p = 8.
Q.6. Given that sin θ = 4 / 5 then find the value of cos θ. (1 Mark)
Ans. Given, sin θ = 4 / 5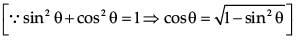
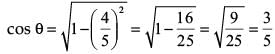
Q.7. If sin θ – cos θ = 0, then find the value of θ. (1 Mark)
OR
What is the value of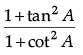 ? (1 Mark)
? (1 Mark)
Ans. Given sin θ − cosθ = 0
⇒ sinθ = cosθ ⇒ sinθ / cosθ = 1
⇒ tan θ = 1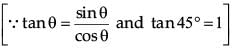
⇒ tan θ = tan 45°
∴ θ = 45°
OR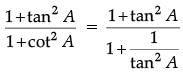
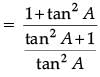
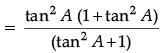
= tan2A.
Q.8. What is the area of the largest triangle that can be inscribed in a semi-circle of radius ‘r’ units? (1 Mark)
OR
A pole 6 m high casts a shadow 2√3 m long on the ground, then find the sun’s elevation. (1 Mark)
Ans. 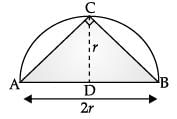 Take a point C on the circumference of the semi-circle and join it by the end points of diameter AB.
Take a point C on the circumference of the semi-circle and join it by the end points of diameter AB.
∠C= 90° [Angle in a semi-circle is right angle]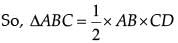
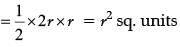
OR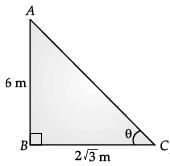 In ΔABC, ∠B = 90°
In ΔABC, ∠B = 90°
tan θ = 6 / 2√3 = √3
tan θ = tan 60°
⇒ θ = 60°
Q.9. If mean is 4 and median is 3 then find the mode. (1 Mark)
Ans. ∵ Mode = 3 Median – 2 Mean
∴ Mode = 3 × 3 – 2 × 4
= 9 – 8 = 1
Q.10. Which term of the A.P., : 21, 42, 63, 84,... is 210? (1 Mark)
Ans. In the given A.P., a = 21, d = 42 – 21 = 21, and tn = 210
Thus,
tn = a + (n - 1)d
⇒ 210 = 21 + (n - 1) 21
⇒ 189 = (n - 1) 21
⇒ n = 10
Q.11. Write the product of √2 and √3: (1 Mark)
Ans.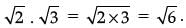
Q.12. If the quadratic polynomial is x2 – 2x – 8, then find the product of zeroes. (1 Mark)
Ans. For quadratic polynomial ax2 + bx + c.
Therefore, for x2 – 2x – 8
Product of zeroes, α × β = (c / a)
= (-8) / 1 = -8.
Q.13. If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in the same ratio, then the two triangles are similar by…… test of similarity. (1 Mark)
OR
If two figures have same shape and same size. Then the figures are said to be .................... . (1 Mark)
Ans. SAS (Side-angle-side) test of similarity.
OR
Congruent.
Q.14. Find the lengths of the tangents drawn from an external point to a circle. (1 Mark)
Ans. The lengths of the tangents drawn from an external point to a circle are 'EQUAL'.
Q.15. If the arithmetic mean of x, x + 3, x + 6, and x + 12 is 10, the find the value of x. (1 Mark)
Ans. According to the question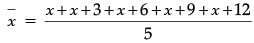
⇒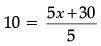
⇒ 5x + 30 = 10 × 5
⇒ 5x = 50 – 30
⇒ x = 4
Q.16. Find the least number that is divisible by all the numbers from 1 to 10 (both inclusive). (1 Mark)
OR
If the pair of linear equations given by kx + 2 = y and 10x – 2y = 12 is inconsistent, then find the value of k. (1 Mark)
Ans. Required number = LCM (1, 2, 3, 4, 5, 6, 7, 8, 9, 10) = 1 × 2 × 2 × 2 × 3 × 3 × 5 × 7 = 2520.
OR
Condition for inconsistency :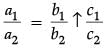
(parallel lines)
For kx + 2 = y and 10x – 2y = 12
k / 10 = -1 / -2 ≠ 2 / -12
∴ – 2k = – 10 or k = 5.
Section - II
Q.17. Five tennis balls, diameter 62 mm are placed in cylindrical card tubes (see in figure)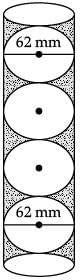
(i) Find the radius of the tennis balls : (1 Mark)
(a) 30 mm
(b) 29 mm
(c) 31 mm
(d) 32 mm
Ans. (c)
Solution. Radius of the tennis balls
= 62 / 2 mm
= 31 mm
(ii) Volume of 1 ball is equal to : (1 Mark)
(a) 125 cm3
(b) 123.5 cm3
(c) 120.30 cm3
(d) 124.84 cm3
Ans. (d)
Solution. Volume of one ball
= 4 / 3 x 22 / 7 x 31 x 31 x 31
= 124838.48 mm3.
= 124.84 cm3.
(iii) Find the height of the tube : (1 Mark)
(a) 300 mm
(b) 320 mm
(c) 310 mm
(d) 301 mm
Ans. (c)
Solution. Height of the tube, h = 5 × diameter of the ball.
h = 5 × 62 = 310 mm.
(iv) Find the volume of the tube : (1 Mark)
(a) 963 cm3
(b) 966.3 cm3
(c) 939.23 cm3
(d) 936.29 cm2
Ans. (d)
Solution. Volume of the tube = πr2h
= 22 / 7 x (31)2 x 310
= 936288.57 mm3
= 936.29 cm3
(v) Find the volume of unfilled space (shaded area) in the tube. (1 Mark)
(a) 310.9 cm3
(b) 312.09 cm3
(c) 301.90 cm3
(d) 321.09 cm3
Ans. (b)
Solution. Volume of unfilled space (shaded area) in the tube
= 936.29 – 624.2
= 312.09 cm3.
Q.18. In a school, an Design exam is conducted in class X. Rubina wins 1st prize. She made a square embroided handkerchief with 9 circular thread designs on it.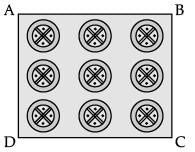
(i) On a square handkerchief, nine circular designs each of radius 7 cm are made (see in figure). Find the circumference of one of the circular design. (1 Mark)
(a) 41 cm
(b) 42 cm
(c) 43 cm
(d) 44 cm
Ans. (d)
Solution. Circumference = 2πr
= 2 x 22 / 7 x 7
= 44 cm.
(ii) Find the total area of 9 circles if radius of each circle is 7 cm. (1 Mark)
(a) 1380 cm2
(b) 1385 cm2
(c) 1386 cm2
(d) 1384 cm2
Ans. (c)
Solution. Area of 9 circles = 9 × πr2
= 9 x 22 / 7 x (7)2
= 1386 cm2.
(iii) The area of circle having 'r' is equal to : (1 Mark)
(a) πr2
(b) πr3
(c) 2πr2
(d) 3πr2
Ans. (a)
Solution. Area of circle = πr2
(iv) If radius of circle is 4r, the area of circle is equal to : (1 Mark)
(a) 50.20 r2 sq. units
(b) 50.28 r2 sq. units
(c) 51.24 r2 sq. units
(d) 52.24 r2 sq. units
Ans. (b)
Solution. Area of circle = πR2
= π(4r)2
= 22 / 7 x 16 x r2
= 58.28 sq. units.
(v) Area of square is equal to : (1 Mark)
(a) 4a
(b) a2
(c) 2a
(d) 3a
Ans. (b)
Solution. Area of square = a × a = a2.
Q.19. The given figure shows the arrangement of chairs in a classroom. Dinesh, Mohan and Sohan are seated at A (1, 1), B (– 2, 7) and C (3, – 3) respectively.
(i) Find the distance between Dinesh and Sohan. (1 Mark)
(a) 2√5 units
(b) 2√3 units
(c) 2√7 units
(d) 3√2 units
Ans. (a)
Solution. Distance between Dinesh and Sohan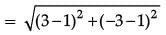
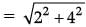
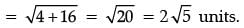
(ii) Find the distance between Dinesh and Mohan. (1 Mark)
(a) 5√3 units
(b) 5√2 units
(c) 3√5 units
(d) 2√5 units
Ans. (c)
Solution. Distance between Dinesh and Mohan.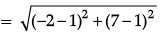

(iii) Name the quadrant in which Sohan is seated. (1 Mark)
(a) I quadrant
(b) II quadrant
(c) III quadrant
(d) IV quadrant
Ans. (d)
Solution. Sohan, C (3, – 3), (IV) quadrant.
(iv) Name the quadrant in which Dinesh is seated. (1 Mark)
(a) I quadrant
(b) II quadrant
(c) III quadrant
(d) IV quadrant
Ans. (a)
Solution. Dinesh, A (1, 1), I quadrant.
(v) Which of the following is the correct distance formula. (1 Mark)
(a)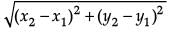
(b) [(x1 – x2) + (y1 – y2)]2
(c) (x1 + x2)2 + (y1 – y2)2
(d) (x1 – x2) – (y1 + y2)2
Ans. (a)
Solution. Distance =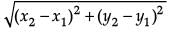
Q.20. From a point on a bridge across a river, the angle of depression of the banks on opposite sides of the river 30° and 45°, respectively. 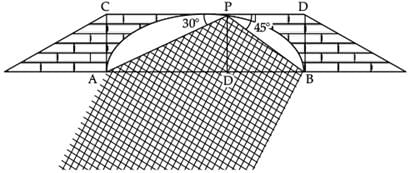
(i) If the bridge is at a height of 3 m from the banks, find the width of the river. (1 Mark)
(a) 2 (√3 + 1) m
(b) (√3 + 1) m
(c) (√3 + 2) m
(d) 3 (√3 + 1) m
Ans. (d)
Solution. In right ΔAPD
∠A = 30°
So, tan 30° = PD / AD
1 / √3 = PD / AD ⇒ 1 / √3 = 3 / AD
AD = 3√3 m
Also, in right ΔPBD,
∠B = 45°
So, tan 45° = PD / BD
⇒ 1 = 3 / BD
⇒ BD = 3 m
Now, AB = AD + BD
⇒ AB = 3√3 + 3 = 3 (√3 +1) m.
(ii) Name the ΔAPD. (1 Mark)
(a) Acute Angled triangle
(b) Right Angled triangle
(c) Obtuse Angled triangle
(d) Equilateral triangle
Ans. (b)
Solution. Right angled triangle.
(iii) In ΔAPD, tan 30° = ? (1 Mark)
(a) AD / DP
(b) AP / AD
(c) PD / AD
(d) AD / AP
Ans. (c)
Solution. In, ΔAPD, tan 30° = Perpendicular / Base
= PD / AD
(iv) The value of tan 45° is equal to : (1 Mark)
(a) 0
(b) 2
(c) 1
(d) 1 / √3
Ans. c
Solution. tan 45° = 1
(v) The value of tangent in right angle triangle is equal to : (1 Mark)
(a) Perpendicular / Base
(b) Base / Perpendicular
(c) Hypotenuse / Base
(d) Perpendicular / Hypotenuse
Ans. (a)
Solution. Perpendicular / Base
Part - B
Q.21. Find the zeroes of the quadratic polynomial 4√3x2 + 5x – 2√3. (2 Mark)
OR
A cylinder and a cone have base radii 5 cm and 3 cm respectively and their respective heights are 4 cm and 8 cm. Find the ratio of their volumes. (2 Mark)
Ans. Given polynomial is
p(x) = 4√3x2 + 5x – 2√3
As,
p(x) = 0
4√3x2 + 8x – 3x – 2√3 = 0
4x (√3 x + 2) – √3 (√3 x + 2) = 0
(√3 x + 2)(4x – √3) = 0
x = (-2 / √3) or (√3 / 4)
∴ Zeroes are (-2 / √3) or (√3 / 4)
OR
Volume of cylinder = π(5)2 × 4cm3
= 100πcm3.
Volume of cone = 1 / 3 ≠ x 32 x 8
= 24π cm
∴ Required ratio = 100π : 24π
= 25 : 6.
Q.22. Find the value of k for which the roots of the quadratic equation 2x2 + kx + 8 = 0 will have the equal roots? (2 Mark)
Ans. An equation has equal roots if the discriminant b2 – 4ac = 0
In the given equation, 2x2 + kx + 8 = 0
a = 2, b = k, c = 8
∴ discriminant = k2 – 4 (2) (8) = 0
= k2 – 64 = 0
= k2 = 64 or k = ± 8
Q.23. Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5. (2 Mark)
Ans. The sequence goes like this, 110, 120, 130,................., 990
Since, they have a common difference of 10, they form an A.P. a = 110, an = 990 and d = 10
∵ an = a+ (n – 1) × d
∴ 990 = 110 + (n – 1) × 10
or, 990 – 110 = (n – 1) × 10
or, 880 = (n – 1) × 10
or, n – 1 = 88
or, n = 89
Hence, there are 89 terms between 101 and 999 which are divisible by both 2 and 5.
Q.24. Find the ratio in which the y-axis divides the line segment joining the points (– 4, – 6) and (10, 12). Also, find the coordinates of the point of division. (2 Mark)
OR
Find the area of circle whose circumference is 22 cm. (2 Mark)
Ans. Let the point on the y-axis which divides the line segment joining the points A(– 4, – 6) and B(10, 12) be C(0, y).
Let the ratio in which y-axis divides AB line segment be k : 1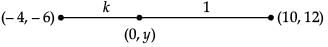
By section formula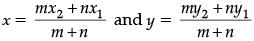
∴ 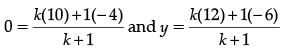
∴ 10k – 4 = 0 or k = 2 / 5
and 12k – 6 = y [(2 / 5) + 1] (substitute value of k)
12(2 / 5) - 6 = y(7 / 5)
y = -6 / 7
∴ (0, y) = (0, -6 / 7)
Thus, the line segment joining the points (– 4, – 6) and (10, 12) divided by the y-axis in the ratio 2 : 5 internally and the coordinates of the point of division is (0, -6 / 7)
OR
Circumference (C) = 22 cm
⇒ 2πr = 22 cm
⇒ r = 7 / 2 cm
Area of circle = πr2
= 22 / 7 x (7 / 2)2 = 77 / 2 cm2
Q.25. If sin (A + B) = 1 and sin (A – B) = 1 / 2 , 0 ≤ A + B = 90° and A > B, then find A and B. (2 Mark)
Ans. Here, sin (A + B) = 1
= sin 90°
or, A + B = 90° ...(i)
sin (A – B) = 1 / 2
= sin 30°
or, A – B = 30° ...(ii)
Solving eq. (i) and (ii),
A = 60° and B = 30°
Q.26. Calculate the median from the following data : (2 Mark)
Ans. 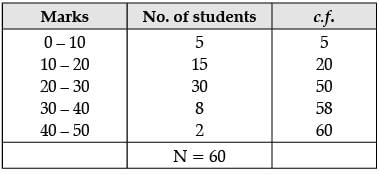
Median = N / 2 = 60 / 2 = 30
The cumulative frequency just greater than 30 is 50 and the corresponding class is 20 – 30.
So, Median class = 20 – 30
l = 20, f = 30, c.f. = 20 and h = 10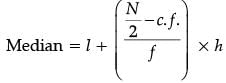
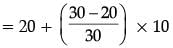
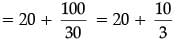
= 20 + 3.33
∴ Median = 23.33
All questions are compulsory. In case of internal choices, attempt anyone.
Q.27. The HCF of 65 and 117 is expressible in the form 65 m – 117. Find the value of m. Also find the LCM of 65 and 117 using prime factorization method. (3 Mark)
OR
Prove that √2 is an irrational number. (3 Mark)
Ans. Since, 117 = 13 × 3 × 3 and 65 = 13 × 5
∴ HCF (117, 65) = 13
Given, HCF = 65 m – 117
Then, 13 = 65 m – 117
65 m = 117 + 13 =130
m = 130 / 65 = 2
Hence, LCM(117, 65) = 13 × 5 × 3 × 3 = 585.
OR
Let us assume √2 be a rational number and its simplest form be a / b, a and b are co-prime positive integers and b ≠ 0.
So, √2 = a / b
⇒ a2 = 2b2
Thus a2 is a multiple of 2
⇒ a is a multiple of 2.
Let a = 2 m for some integer m
∴ b2 = 2m2
Thus b2 is a multiple of 2
⇒ b is a multiple of 2
Hence √2 is a common factor of a and b.
This contradicts the fact that a and b are co-primes.
Hence √2 is an irrational number.
Q.28. Determine the AP whose fifth term is 19 and the difference of the eighth term from the thirteenth term is 20. (3 Mark)
Ans. Let a and d are first term and common difference of an A . P.
nth term = an = a + (n – 1)d ...(1)
(i) Given a5 = 19
a + 4d = 19 ...(2)
(ii) Difference of the eighth term from the thirteenth term = 20
a13 – a8 = 20
a + 12d – ( a + 7d ) = 20
a + 12d – a – 7d = 20
5d = 20 or d = 4
Put d = 4 in (2)
a + 4d = 19
a + (4 × 4) = 19
a + 16 = 19
a = 19 – 16 or a = 3
Therefore, a = 3 , d = 4
Required A .P is
a, a + d, a + 2d, a + 3d, .....
3, 7, 11, 15, 19 , ....
Q.29. Find the point on y-axis which is equidistant from the points (6, 5) and (– 4, 3). (3 Mark)
Ans. Let the point on y axis is P(0, y) which is equidistant from the points A(6, 5) and B(– 4, 3).
The distance between PA is equal to PB such that, PA = PB
By distance formula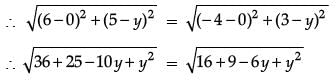
61 – 10y = 25 – 6y
4y = 36 or y = 9
So, the point P(0, 9) is equidistant from the points A(6, 5) and B(– 4, 3).
Q.30. ABC is a triangle. A circle touches sides AB and AC produced and side BC at X, Y and Z respectively. Show that AX = 1 / 2 perimeter of ΔABC. (3 Mark)
Ans. 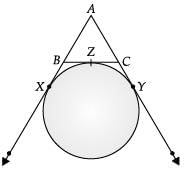 Perimeter of ΔABC = AB + AC + BC = (AX – BX) + (AY – CY) + (BZ + ZC).
Perimeter of ΔABC = AB + AC + BC = (AX – BX) + (AY – CY) + (BZ + ZC).
= AX + AY – BX + BZ + ZC – CY
The tangents of a circle, from an external point are equal.
From point B → BX = BZ From A → AX = AY and from point C → CZ = CY
∴ P = AX + AY = 2AX
or AX = 1 / 2 Perimeter of ΔABC.
Q.31. Find A and B if sin (A + 2B) = √3 / 2 and cos (A + 4B) = 0, where A and B are acute angles. (3 Mark)
Ans. Given, sin(A + 2B) = √3 / 2
⇒ sin (A + 2B) = sin 60°
[∵ sin 60° = √3 / 2]
⇒ A + 2B = 60° ...(i)
Also, given cos (A +4B) = 0
⇒ cos (A + 4B) = cos 90° [∵ cos 90° = 0]
⇒ A + 4B = 90°
By subtracting equation (ii) from equation (i)
A + 2B – (A +4B) = 60° – 90°
⇒ –2B = –30°
⇒ B = 15°
From eq(i),
A + 2(15°) = 60°
⇒ A = 60° – 30° = 30°
Hence angle A = 30° and angle B = 15°.
Q.32. In the fig., PSR, RTQ and PAQ are three semi-circles of diameters 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region. (Use π = 22 / 7) (3 Mark) OR
OR
Two spheres of same metal weight 1 kg and 7 kg. The radius of the smaller sphere is 3 cm. The two spheres are melted to form a single big sphere. Find the diameter of the new sphere. (3 Mark)
Ans. Perimeter of shaded region = Perimeter of semi-circle PSR + Perimeter of semi circle RTQ + Perimeter of semi circle PAQ
= π × 5 + π(1.5) + π(3.5)
= (5 + 5)π
= 10π
= 22 / 7 x 10
= 31.43 cm
OR
Radius of 1st sphere = 3 cm
∴ 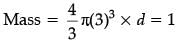
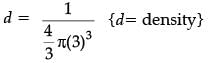
Let radius of 2nd sphere be r cm
∴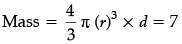
⇒ r3 = 7 (3)3
Volume of two spheres = Volume of new sphere of radius (R)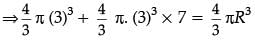
⇒ R3 = (3)3 (1+7)
⇒ R = 3(2) = 6
∴ Diameter = 12 cm
Q.33. Find x and y from the following cumulative frequency distribution : (3 Mark)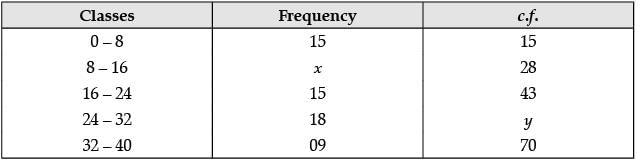
Ans. From the cumulative frequency distribution,
15 + x = 28
⇒ x = 28 – 15 = 13
and 43 + 18 = y
⇒ y = 61
Hence, x = 13 and y = 61.
All questions are compulsory. In case of internal choices, attempt anyone.
Q.34. Find the value of a, b and c such that the numbers a, 10, b, c, 31 are in A.P. (5 Mark)
OR
If a and b are the zeroes of the polynomial x2 + 4x + 3, find the polynomial whose zeroes are 1 + β / α and 1 + α / β. (5 Mark)
Ans. Since a, 10, b, c, 31 are in A.P.
Let common difference be d.
a + d = 10 ...(i)
a + 4d = 31 ...(ii)
Solving (i) & (ii) we get
3d = 21 or d = 7 and a = 10 – 7 or a = 3
∴ Third term b = a + 2d
= 3 + 2(7)
= 17
Also, fourth term c = a + 3d
= 3 + 3(7)
= 24
So the AP is: 3, 10, 17, 24, 31.
OR
Since, a and b are the zeroes of the quadratic polynomial x2 + 4x + 3
Comparing it with ax2 + bx + c
a = 1 , b = 4, c = 3
So,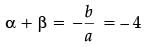
and αβ = c / a = 3
Sum of zeroes of new polynomial
= 1 + β / α + 1 + α / β
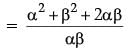
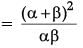
= (-4)2 / 3 = 16 / 2
Product of zeroes of new polynomial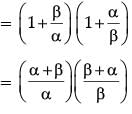

= (-4)2 / 3 = 16 / 2
So, required polynomial = x2 – (Sum of the zeroes) x + Product of the zeroes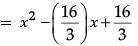

= 1 / 3(3x2 - 16x + 16).
Q.35. Find the coordinates of the point which divide the line segment joining A(– 4, 1) and B(8, 7) into three equal parts. (5 Mark)
Ans. Let P(x1, y1) and Q(x2, y2) are two points which divide AB in three equal parts.
P divides AB in the ratio of 1 : 2 and Q divides AB in the ratio 2 : 1.
By section formula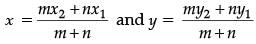
∴ 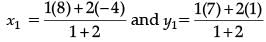
x1 = 0 and y1 = 3
∴ P(x1, y1) = (0, 3)
Similarly, by section formula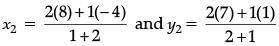
∴ x2 = 4 and y2 = 5
∴ Q(x2, y2) = (4, 5)
Q.36. A man in a boat rowing away from a light house 100 m high takes 2 minutes to change the angle of elevation of the top of the light house from 60° to 30°. Find the speed of the boat in metres per minute. [Use 3 = 1.732] (5 Mark)
Ans. Height of the light house, h = 100 m
Let initial distance be x m and the angle is 60°
From ΔDBC, ∠B = 90°
So, tan 60° = h / x
⇒ √3 = 100 / x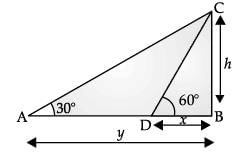
⇒ x = 100 / √3
Now, after time 2 min , let the new distance be y and angle is 30°
From ΔABC, ∠B = 90°
So, tan 30° = h / y
⇒ 1 / √3 = 100 / y
⇒ y = 100√3
Therefore, distance (d) travelled in 2 min = y – x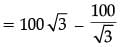
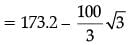
= 173.2 – 57.73
= 115.47 m
Given, t = 2 min
∴ Speed = d / t = 115.47m / 2 min
= 57.74 m/min
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Mathematics: CBSE Sample Question Paper (2020-21) (Basic) - 3 - Mathematics (Maths) Class 10
| 1. What is the format of the CBSE Sample Question Paper for Class 10 Mathematics (Basic)? |  |
| 2. How many sections are there in the CBSE Sample Question Paper for Class 10 Mathematics (Basic)? |  |
| 3. What is the weightage of Section A in the CBSE Sample Question Paper for Class 10 Mathematics (Basic)? |  |
| 4. What is the difference between Section B and Section C in the CBSE Sample Question Paper for Class 10 Mathematics (Basic)? |  |
| 5. Is the CBSE Sample Question Paper for Class 10 Mathematics (Basic) based on the latest syllabus? |  |
















