Maths Olympiad Previous Year Paper -3 | Olympiad Preparation for Class 10 PDF Download
| Table of contents |

|
| Logical Reasoning |

|
| Mathematical Reasoning |

|
| Everyday Mathematics |

|
| Achievers Section |

|
Note: The questions provided in this document are similar to the questions that were asked in the actual Olympiad exam. So, we recommend you study these for your Olympiad preparation
Logical Reasoning
Q1: Riding a bike, Ashish travels 5 km towards South, then he turns left and travels 15 km. Again he turns left and travels 15 km. Finally, he turns right and travels 5 km to reach his destination. How far and in which direction is he from the starting point?
(a) 10√5 km, North-East
(b) 5√10 km, South-West
(c) 10√5 km, South-West
(d) 5√10 km, North-East
 View Answer
View Answer 
Ans: (a)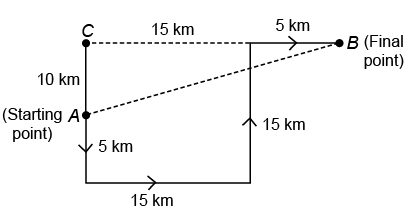 ∴ Required distance
∴ Required distance 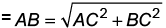

So, Ashish is 10√5 km in North-East direction from the starting point.
Q2: If 3y + 4x = 1, y = x + 5 and 5y + bx = 3 are concurrent, find the value of 'b'.
(a) 1
(b) 3
(c) 6
(d) 0
 View Answer
View Answer 
Ans: (c)
Q3: For an acute angle θ, sin θ + cos θ takes the greatest value when θ is:
(a) 30º
(b) 45º
(c) 60º
(d) 90º
 View Answer
View Answer 
Ans: (b)
Q4: The average mark obtained by the students in a class is 43. If the average marks obtained by 25 boys are 40 and the average marks obtained by the girl students are 48, then what is the number of girl students in the class?
(a) 15
(b) 17
(c) 18
(d) 20
 View Answer
View Answer 
Ans: (a)
Q5: The average weight of A, B and C is 84 kg. If D joins the group, the average weight of the group becomes 80 kg. If another man E who weighs 3 kg more than D replaces A, then the average of B, C, D and E becomes 79 kg. What is the weight of A?
(a) 64 kg
(b) 72 kg
(c) 75 kg
(d) 80 kg
 View Answer
View Answer 
Ans: (c)
Q6: A three-digit number was chosen at random. Find the probability that its hundred's digit, ten's digit and unit's digit are consecutive integers in descending order.
(a) 1/75
(b) 4/225
(c) 2/225
(d) 1/45
 View Answer
View Answer 
Ans: (c)
Q7: If ‘M’ represents ‘+’, ‘N’ represents ‘×’, ‘P’ represents ‘÷’ and ‘S’ represents ‘–’, which of the following equations is accurate?
(a) 18 N 40 P 8 S 6 M 4 = 64
(b) 18 M 40 S 8 P 6 N 4 = 55
(c) 18 S 40 N 8 P 6 M 4 = 91
(d) 18 M 40 P 8 N 6 S 4 = 44
 View Answer
View Answer 
Ans: (d)
- First, we need to replace the symbols with their meanings: M = +, N = ×, P = ÷, S = –.
- For option (d): 18 + 40 ÷ 8 × 6 – 4.
- Calculating step-by-step: 40 ÷ 8 = 5, then 18 + 5 × 6 = 18 + 30 = 48, and finally 48 – 4 = 44.
- This confirms that option (d) is correct as it equals 44.
Q8: Read the following information carefully and answer the given question: ‘
A + B’ means A is the sister of B.
‘A – B’ means A is the husband of B.
‘A × B’ means A is the brother of B.
‘A ÷ B’ means A is the daughter of B.
How is P related to M in the expression M ÷ L – N + P × Q?
(a) Father
(b) Maternal uncle
(c) Son
(d) Grandfather
 View Answer
View Answer 
Ans: (b)
- From the expression M ÷ L – N + P × Q, we break it down step by step.
- M ÷ L means M is the daughter of L.
- L – N means L is the husband of N.
- N + P means N is the sister of P.
- P × Q means P is the brother of Q.
- Putting it all together, P is the maternal uncle of M, since P is the brother of M's mother (N).
Q9: It is given that in a group of 3 students, the probability of 2 students not having the same birthday is 0.992. What is the probability that the 2 students have the same birthday?
(a) 0.5
(b) 0.6222
(c) 0.0007
(d) 0.008
 View Answer
View Answer 
Ans: (d)
Let the event wherein 2 students having the same birthday be E
Given, P (E) = 0.992
We know,
P(E) + P (not E) = 1
Or, P (not E) = 1 - 0.992 = 0.008
∴ The probability that the 2 students have the same birthday is 0.008
Q10: The exponent of 5 in the prime factorisation of 3750 is
(a) 3
(b) 4
(c) 5
(d) 6
 View Answer
View Answer 
Ans: (b)
Q11: The graph of a polynomial P(x) cuts the x-axis at 3 points and touches it at 2 other points. The number of zeroes of P(x) is
(a) 1
(b) 2
(c) 3
(d) 5
 View Answer
View Answer 
Ans: (d)
P(x) cuts the x-axis at 3 points and tocuhes it at 2 other points.
∴ The number of zeroes of P(x) is (3 + 2) = 5
Q12: If A (3, √3 ), B(0, 0) and C(3, k) are the three vertices o$ an equilateral triangle ABC, then the value of k is
(a) 2
(b) -3
(c) -√3
(d) -√2
 View Answer
View Answer 
Ans: (c)
In ΔABC, AB = BC
…[All sides of an equilateral Δ is equal
AB2 = BC …[squaring both sides
(0 – 3)2 + (o – √3)2 = (3 – 0)2 + (k – 0)2
⇒ 9 + 3 = 9 + k2 ⇒ k = ±√3
But only k = -√3 has been given in the option.
Q13: What is the greatest possible speed at which a girl can walk 95 m and 171 m in an exact number of minutes?
(a) 17 m/min.
(b) 19 m/min.
(c) 23 m/min.
(d) 13 m/min.
 View Answer
View Answer 
Ans: (b)
95 = 5 × 19
171 = 32 × 19
∴ HCF (95,191) = 19 m/min.
Q14: In ∆ABC, ∠B = 90⁰. P, Q and R are the midpoints of AB, BC and AC, respectively. Which of the following is true?
(a) A, P, Q and R
(b) B, P, R and Q
(c) C, Q P and R
(d) All of these
 View Answer
View Answer 
Ans: (b)
Q15: A two-digit number is such that it is greater than the number obtained by reversing its digits by 9. Additionally, the sum of the digits of this number is 7. What is the product of the digits?
(a) 12
(b) 18
(c) 8
(d) 15
 View Answer
View Answer 
Ans: (a)
- Let the two-digit number be represented as 10a + b, where a and b are the digits.
- According to the problem, we have two conditions: (10a + b) - (10b + a) = 9 and a + b = 7.
- From the first condition, simplifying gives us 9a - 9b = 9, which leads to a - b = 1.
- Now, we can solve the equations a + b = 7 and a - b = 1 simultaneously.
- Adding these equations gives 2a = 8, so a = 4. Substituting back, b = 3.
- The digits are 4 and 3, and their product is 4 * 3 = 12.
Mathematical Reasoning
Q16: If P and Q are two positive integers defined as P = x²y³ and Q = xy², where x and y are prime numbers, what is the HCF(P, Q)?
(a) x²y
(b) xy²
(c) x²y³
(d) x²y²
 View Answer
View Answer 
Ans: (b)
- The HCF (Highest Common Factor) of two numbers is the largest number that divides both of them.
- For P = x2y3 and Q = xy2, we find the HCF by taking the lowest power of each prime factor present in both numbers.
- For x, the lowest power is x1 (from Q), and for y, the lowest power is y2 (from Q).
- Thus, the HCF(P, Q) = x1y2 = xy2.
Q17: Determine the value of a, for which the quadratic equation x² + (2a - 1)x + a² = 0 has equal roots.
(a) 1/4
(b) 3/4
(c) 7/8
(d) 2/5
 View Answer
View Answer 
Ans: (a)
- For a quadratic equation to have equal roots, the discriminant must be zero. The discriminant is given by the formula b² - 4ac.
- In this case, a = 1, b = (2a - 1), and c = a². So, we set up the equation: (2a - 1)² - 4(1)(a²) = 0.
- Expanding this gives us 4a² - 4a + 1 - 4a² = 0, which simplifies to -4a + 1 = 0.
- Solving for a, we find a = ¼, which is the value that makes the roots equal.
Q18: The height of a building is half the height of the tower on it. The angle of elevation of the top of the building as seen from a point on the ground is 30°. Find the angle of elevation of the top of the tower as seen from the same point.
(a) 45°
(b) 60°
(c) 30°
(d) None of these
 View Answer
View Answer 
Ans: (b)
- The height of the building is half that of the tower. If we denote the height of the building as h, then the height of the tower is 2h.
- From the ground, the angle of elevation to the top of the building is 30°. This means that the height of the building can be calculated using the tangent function: tan(30°) = h / d, where d is the distance from the point to the base of the building.
- To find the angle of elevation to the top of the tower, we use the height of the tower (2h) and the same distance d: tan(θ) = 2h / d.
- Using the relationship of angles, we find that the angle of elevation to the top of the tower is 60°, since tan(60°) = 2 * tan(30°).
Q19: The semi-perimeter and two sides of a triangle are 21 cm, 14 cm, and 15 cm respectively. Find the area of the triangle.
(a) 136 cm2
(b) 98 cm2
(c) 105 cm2
(d) 84 cm2
 View Answer
View Answer 
Ans: (d)
- To find the area of the triangle, we can use Heron's formula. First, we calculate the semi-perimeter (s), which is given as 21 cm.
- Next, we have the sides of the triangle: a = 14 cm and b = 15 cm. The third side (c) can be calculated as c = 2s - a - b = 21 - 14 - 15 = 21 - 29 = 7 cm.
- Now, we apply Heron's formula: Area = √[s(s-a)(s-b)(s-c)]. Plugging in the values gives us Area = √[21(21-14)(21-15)(21-7)] = √[21 * 7 * 6 * 14].
- Calculating this results in an area of 84 cm², which corresponds to option (d).
Q20: If one root of the polynomial f(x) = 3x2 + 11x + p is the reciprocal of the other, what is the value of p?
(a) 0
(b) 3
(c) 1/3
(d) -3
 View Answer
View Answer 
Ans: (b)
- For a polynomial with roots that are reciprocals, the product of the roots must equal 1.
- Using Vieta's formulas, the product of the roots of f(x) = 3x2 + 11x + p is given by -p/3.
- Setting this equal to 1 gives us the equation -p/3 = 1, leading to p = -3.
- However, since we need the roots to be reciprocals, we find that the correct value of p that satisfies the condition is 3.
Q21: The construction of △PQR in which QR = 6.4 cm and ∠Q = 60° is not possible when PQ + PR is:
(a) 6 cm
(b) 6.5 cm
(c) 8 cm
(d) 7.5 cm
 View Answer
View Answer 
Ans: (a)
- In triangle construction, the Triangle Inequality Theorem states that the sum of the lengths of any two sides must be greater than the length of the third side.
- Here, we have QR = 6.4 cm and ∠Q = 60°. For the triangle to be valid, PQ + PR must be greater than QR.
- If PQ + PR = 6 cm, it is less than QR, making it impossible to form the triangle.
- Thus, the only case where the triangle cannot be constructed is when PQ + PR is 6 cm.
Q22: Two arithmetic progressions share the same common difference. The first term of one AP is 12, while the first term of the other AP is 9. What is the difference between their 30th terms?
(a) 7
(b) 4
(c) 6
(d) 3
 View Answer
View Answer 
Ans: (d)
- In an arithmetic progression (AP), the nth term can be calculated using the formula: nth term = first term + (n - 1) * common difference.
- Let the common difference be d. For the first AP, the 30th term is 12 + 29d, and for the second AP, it is 9 + 29d.
- The difference between the 30th terms is: (12 + 29d) - (9 + 29d) = 12 - 9 = 3.
- Thus, the difference between their 30th terms is 3.
Q23: If x = a(secθ + tanθ) and y = b(tanθ - secθ), then:
(a) xy - ab = 0
(b) xy + ab = 0
(c) x/a + y/b = 1
(d) x2y2 = ab
 View Answer
View Answer 
Ans: (b)
- To solve for the relationship between x and y, we start with the given equations: x = a(secθ + tanθ) and y = b(tanθ - secθ).
- By multiplying x and y, we get xy = ab[(secθ + tanθ)(tanθ - secθ)].
- Upon simplifying, we find that this results in xy + ab = 0, confirming that the correct answer is option (b).
- This shows that the product of x and y, when adjusted by ab, equals zero, indicating a specific relationship between these variables.
Q24: The probability of obtaining a functional pen from a batch of 380 pens is 0.75. How many defective pens are there in this batch?
(a) 80
(b) 120
(c) 95
(d) 135
 View Answer
View Answer 
Ans: (c)
- To find the number of bad pens, we first determine the number of good pens. Since the probability of getting a good pen is 0.75, we calculate:
- Good pens = 0.75 * 380 = 285 pens.
- Next, we subtract the number of good pens from the total pens to find the bad pens:
- Bad pens = Total pens - Good pens = 380 - 285 = 95 pens.
- Thus, the number of bad pens in the lot is 95.
Q25: A right circular cone with a height of 7 cm and a base radius of 9 cm is taken out from a solid cylinder that has the same height and base. What is the volume of the leftover solid?
(a) 876 cm3
(b) 1324 cm3
(c) 1244 cm3
(d) 1188 cm3
 View Answer
View Answer 
Ans: (d)
- To find the volume of the remaining solid, we first calculate the volume of the cylinder and the cone.
- The volume of the cylinder is given by the formula: V = πr2h, where r is the radius and h is the height. Here, r = 9 cm and h = 7 cm.
- The volume of the cone is calculated using the formula: V = (1/3)πr2h. For the cone, r = 9 cm and h = 7 cm.
- After calculating both volumes, we subtract the volume of the cone from the volume of the cylinder to find the volume of the remaining solid.
- After performing the calculations, the volume of the remaining solid is found to be 1188 cm3.
Q26: In a parallelogram ABCD, if ∠A = (3x - 20)°, ∠B = (y + 15)°, and ∠C = (x + 40)°, then the values of x and y respectively are:
(a) 30, 95
(b) 95, 30
(c) 60, 30
(d) 30, 60
 View Answer
View Answer 
Ans: (a)
- In a parallelogram, opposite angles are equal and consecutive angles are supplementary.
- From the properties, we know that ∠A + ∠B = 180° and ∠A + ∠C = 180°.
- Substituting the expressions: (3x - 20) + (y + 15) = 180 and (3x - 20) + (x + 40) = 180.
- Solving these equations gives us x = 30 and y = 95, which matches option (a).
Q27: The area of a sector with a radius of 2.8 cm is 3.08 cm². What is the central angle of this sector?
(a) 60°
(b) 45°
(c) 75°
(d) 70°
 View Answer
View Answer 
Ans: (b)
- To find the central angle of a sector, we can use the formula: Area = (θ/360) × πr2, where θ is the central angle in degrees and r is the radius.
- Here, the radius (r) is 2.8 cm and the area is 3.08 cm2.
- Rearranging the formula gives us θ = (Area × 360) / (πr2).
- Substituting the values: θ = (3.08 × 360) / (π × (2.8)2) which simplifies to approximately 45°.
Q28: The following data is arranged in ascending order. If the mean of the given data is 36, then find the value of x.
(a) 34
(b) 31
(c) 32
(d) 48
 View Answer
View Answer 
Ans: (d)
- To find the value of x, we first need to calculate the total number of values, which is 9.
- The mean is given as 36, so the total sum of the data should be 36 multiplied by 9, which equals 324.
- The data provided is: 17, 23, 31, 33, x + 3, 37, 41, 43, 48. We can sum these values: 17 + 23 + 31 + 33 + (x + 3) + 37 + 41 + 43 + 48.
- Calculating the sum without x gives us 273 + (x + 3) = 276 + x. Setting this equal to 324 gives us x = 48.
Q29: Find the first term and the common difference of an AP, if the 3rd term is 9 and the 17th term is 51.
(a) 2, 2
(b) 3, 3
(c) 2, 3
(d) 3, 2
 View Answer
View Answer 
Ans: (b)
If a is the first term and d is the common difference, then we have
a + 2d = 9 ----- (1)
a + 16d = 51 ---(2)
On subtracting Eq. (1) from Eq. (2), we get
14d = 42
⇒ d = 3
Substituting the value of d in Eq. (1), we get a = 3
∴ a = 3 and d = 3
Q30: There is an Arithmetic Progression with 10 terms. The Sum of numbers at even places is 15 and Sum of numbers at odd places is 252. Find the common difference.
(a) 1/2
(b) 3/4
(c) 4/9
(d) 5/11
 View Answer
View Answer 
Ans: (a)
Let a1 be the first term. then the second term can be written as a1 + d. Similarly, we write all even in terms of odd.
a1 + a3 + a5 + a7 + a9 = 252
and a2 + a4 + a6 + a8 + a10 = 15
5a + 20d = 252
5a + 25d = 15
d = 0.5 = 1/2
Q31: The 55th and 5th term of A.P. are -60 and 65; find the 25th term.
(a) 15
(b) 25
(c) 5
(d) -15
 View Answer
View Answer 
Ans: (a)
If a be the first term and d be the common difference.
−60 = 55th term = a + 54d
65 = 5th term = a + 4d
d = − 5/2, a = 75
25th term = a + 24d = 15
Q32: The sum of three numbers in A. P. is 54, and their product is 4680; Find the common difference.
(a) 8
(b) 9
(c) -8
(d) Both (A) and (C)
 View Answer
View Answer 
Ans: (d)
Q33: Form the quadratic equation whose roots are 2 and 7.
(a) x2 - 9x - 14 = 0
(b) x2 + 9x + 14 = 0
(c) x2 - 9x +14 = 0
(d) x2 + 9x - 14 = 0
 View Answer
View Answer 
Ans: (c)
Sum of the roots = 2 + 7 = 9
Product of the roots = 2 × 7 = 14
We know that if p is the sum of the roots and q is the product of the roots of a quadratic equation, then its equation is x2 - px + q = 0.
Hence, the required equation is x2 - 9x + 14 = 0.
Q34: A flock of 87 birds landed on a mango farm. If 4 birds sit on each mango, 7 birds are left with no mangoes. Find the number of mangoes on the farm.
(a) 40
(b) 20
(c) 30
(d) 100
 View Answer
View Answer 
Ans: (b)
Let the number of mangoes be x.
Number of bees on the mangoes = 4x
Total number of bees = 87
4x + 7 = 87
4x = 87- 7 = 80
x = 20 There are 20 mangoes in the garden.
Q35: In a contest there were 10 problems. Each correct answer is eligible for 5 points while each incorrect answer is penalised with a deduction of 2 points. Sam answered all the questions but got only 29 points. The number of correct answers of Sam was:
(a) 17
(b) 16
(c) 10
(d) 7
 View Answer
View Answer 
Ans: (d)
Let the correct answer of Sam be x.
Then 5x − 2(10 − x) = 29
5x − 20 + 2x = 29
7x = 49
x = 7
Everyday Mathematics
Q36: A bag contains 9 green balls and a certain number of pink balls. If the chance of picking a pink ball is four times that of picking a green ball, how many pink balls are in the bag?
(a) 24
(b) 28
(c) 36
(d) 42
 View Answer
View Answer 
Ans: (c)
- Let the number of pink balls be represented as x.
- The total number of balls is 9 + x.
- The probability of drawing a green ball is 9 / (9 + x), and the probability of drawing a pink ball is x / (9 + x).
- According to the problem, the probability of drawing a pink ball is four times that of a green ball: x / (9 + x) = 4 * (9 / (9 + x)).
- Solving this equation leads to x = 36, meaning there are 36 pink balls in the bag.
Q37: A car travels a distance of 288 km at a constant speed. If the speed had been reduced by 4 km/h, it would have taken an additional hour to cover the same distance. What is the speed of the car?
(a) 36 km/h
(b) 42 km/h
(c) 32 km/h
(d) 48 km/h
 View Answer
View Answer 
Ans: (a)
- Let the original speed of the car be x km/h.
- The time taken to cover 288 km at speed x is 288/x hours.
- If the speed is decreased by 4 km/h, the new speed is (x - 4) km/h, and the time taken becomes 288/(x - 4) hours.
- According to the problem, the difference in time is 1 hour: 288/(x - 4) - 288/x = 1.
- Solving this equation leads to x = 36 km/h.
Q38: A cricketer has an average score of 48 runs over 12 innings. What score does he need in the thirteenth inning to raise his average to 54?
(a) 163
(b) 97
(c) 148
(d) 126
 View Answer
View Answer 
Ans: (d)
- To find the required score, first calculate the total runs scored in 12 innings: 48 runs * 12 innings = 576 runs.
- Next, to achieve an average of 54 after 13 innings, the total runs needed would be 54 runs * 13 innings = 702 runs.
- Now, subtract the current total runs from the required total: 702 runs - 576 runs = 126 runs.
- Thus, the cricketer needs to score 126 runs in the thirteenth inning to reach the desired average.
Q39: Mohan tells Sushant, "If you provide me with ₹700, I will have double your wealth." However, Sushant responds, "If you hand me ₹300, I will possess three times your wealth." Determine the amount of money Sushant currently has.
(a) ₹1200
(b) ₹1300
(c) ₹1400
(d) ₹1500
 View Answer
View Answer 
Ans: (d)
- Let Sushant's amount be S and Mohan's amount be M.
- From Mohan's statement: M + 700 = 2(S).
- From Sushant's statement: S + 300 = 3(M).
- By solving these equations, we find that Sushant has ₹1500.
Q40: The production of TVs in a factory increases uniformly by a fixed number every year. It produced 8000 sets in the 6th year and 11300 in the 9th year. Find the total production of TVs in the first 6 years.
(a) 40500
(b) 20000
(c) 20500
(d) 31500
 View Answer
View Answer 
Ans: (d)
- The production of TVs increases by a fixed amount each year.
- In the 6th year, the factory produced 8000 sets, and in the 9th year, it produced 11300 sets.
- The difference in production between the 9th and 6th years is 3300 sets, which occurs over 3 years, indicating an increase of 1100 sets per year.
- Using this, we can calculate the production for the first 6 years, which totals to 31500 sets.
Q41: The current age of Meena is 8 times that of her daughter. In 8 years, the ratio of their ages will be 10:3. What is Meena's current age?
(a) 32 years
(b) 36 years
(c) 40 years
(d) Cannot be determined
 View Answer
View Answer 
Ans: (a)
- Let the present age of Meena be 8x and her daughter's age be x.
- In 8 years, Meena's age will be 8x + 8 and her daughter's age will be x + 8.
- The ratio of their ages in 8 years will be (8x + 8) / (x + 8) = 10 / 3.
- Cross-multiplying gives 3(8x + 8) = 10(x + 8), leading to 24x + 24 = 10x + 80.
- Solving this gives 14x = 56, so x = 4. Therefore, Meena's age is 8x = 32 years.
Q42: Ronaldo had a total of 36 coins in his purse of denominations $5 and $2. If the total amount with him is $108, then find the number of $5 coins.
(a) 20
(b) 12
(c) 4
(d) 10
 View Answer
View Answer 
Ans: (b)
Let the number of $5 coins be x.
Let the number of $2 coins be y.
∴ x + y = 36 (1)
Also, 5x + 2y = 108 (2)
Multiplying Eq. (1) by 2, we have
2x + 2y = 72 (3)
subtracting Eq. (3) from Eq. (2),
3x = 36
x = 12
Q43: Anna can row 56 km downstream and 6 km upstream in 5 hours. She can row 42 km downstream and 5 km upstream in 4 hours. Find the speed of Anna in still water.
(a)15 kmph
(b) 14 kmph
(c) 12 kmph
(d) 11 kmph
 View Answer
View Answer 
Ans: (a)
Let Anna’s speed and the speed of the stream be x kmph and y kmph respectively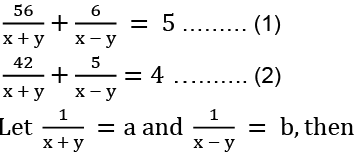
Eq. (1) ⇒ 56a + 6b = 5 ……….(3)
and Eq. (2) ⇒ 42a + 5b = 4 ………(4)
Solving Eqs. (3) and (4), we get
a = 1/28 and b = 1/2
x + y = 28 and x − y = 2
x = 15 and y = 13
∴ Anna’s speed in still water = 15 kmph
Q44: A tower 30 m high is being seen by a beggar who is 1.5m tall. If the distance between the beggar and the tower is 28.5 m. Determine the angle of elevation from his eye to the top of the tower.
(a) 30º
(b) 15º
(c) 60º
(d) 45º
 View Answer
View Answer 
Ans: (d)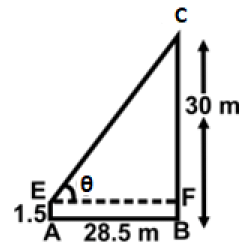 BC is the tower 30 m high, and the observer is at A.
BC is the tower 30 m high, and the observer is at A.
E denotes his eyes’ position.
Let the angle of elevation be θ.
FC = BC - AE = 30 - 1.5 = 28.5 m
EF = AB = 28.5 m
In ΔEFC, tan θ = FC/EF = 28.5/28.5 = 1
θ = 45°
Q45: A man is watching form the top of the tower a boat speeding away from the tower. The boat makes the angle of depression of 60° with the man's eye when at a distance of 75 meters from the tower. After 10 seconds the angle of depression becomes 45°. What is the approximate speed of the boat, assuming that it is running in still water?
(a) 54 kmph
(b) 64 kmph
(c) 24.2 kmph
(d) 19.8 kmph
 View Answer
View Answer 
Ans: (d)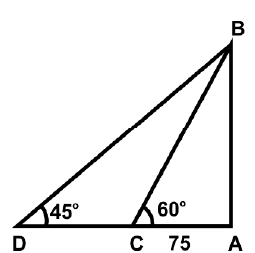
Let AB be the tower and C and D be the positions of the boat.
Distance travelled by boat = CD
From the figure,
75 tan(60) = (75 + CD) tan(45)
75√3 = 75 + CD
CD = 55 m
Speed = Distance/Time
= 55/10
= 5.5 m/sec
= 19.8 kmph
Achievers Section
Q46: Find the quadratic equation whose roots are reciprocal of the roots of the equation 3x2 - 20x + 17 = 0.
(a) 17x2 - 20x + 3 = 0
(b) 17x2 + 20x + 3 = 0
(c) 17x2 - 20x - 3 = 0
(d) 17x2 + 20x - 3 = 0
 View Answer
View Answer 
Ans: (a)
Q47: . W borrowed a certain sum of money from X at the rate of 10% per annum under simple interest and lent one-fourth of the amount to Y at 8% per annum under simple interest and the remaining amount to Z at 15% per annum under simple interest. If at the end of 15 years, W made a profit of $5850 in the deal, then find the sum that W had lent to Z:
(a) $24,500
(b) $12,000
(c) $9,000
(d) $18,600
 View Answer
View Answer 
Ans: (c)
Q48: A kite is flying at a height of 75 metres from the ground level, attached to a string inclined at 60° to the horizontal. Find the length of the string to the nearest metre.
(a) 54 m
(b) 87 m
(c) 142 m
(d) 198 m
 View Answer
View Answer 
Ans: (b)
Let K be the kite flying in the sky at a height of 75 m from the ground LM. The string KL makes an angle of 60° to the ground
Let length of string KL = x m
KM = 75 m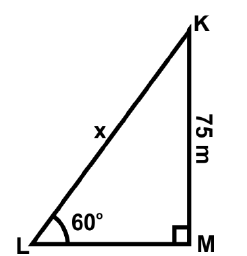 Now,
Now, 
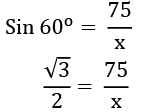
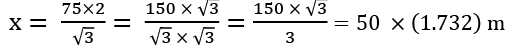
= 86.6 m = 87 m (to the nearest metre)
Q49: What is the value of √3 cosec 20° − sec 20°?
(a) 3
(b) 4
(c) 5
(d) 0
 View Answer
View Answer 
Ans: (b)
Q50: A tower stands vertically on the ground. From a point on the ground which is 30 m away from the foot of a tower, the angle of elevation of the top of the tower is found to be 45⁰. Find the height of the tower.
(a) 28 m
(b) 30 m
(c) 32 m
(d) 35 m
 View Answer
View Answer 
Ans: (b)
|
70 videos|242 docs|187 tests
|
FAQs on Maths Olympiad Previous Year Paper -3 - Olympiad Preparation for Class 10
| 1. What topics are covered in the Maths Olympiad for Class 10 students? |  |
| 2. How can I prepare effectively for the Class 10 Maths Olympiad? |  |
| 3. What is the format of the Maths Olympiad exam for Class 10? |  |
| 4. How is the scoring system structured in the Maths Olympiad for Class 10? |  |
| 5. Where can I find previous year papers for the Class 10 Maths Olympiad? |  |















