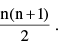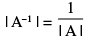Overview: Matrices | Mathematics (Maths) for JEE Main & Advanced PDF Download
Definition
- A set of numbers or objects or symbols represented in the form of a rectangular array is called a matrix.
- The order of the matrix is defined by the number of rows and number of columns present in the rectangular array of representation.
- Unlike determinants, it has no value.
- A matrix of order m × n, i.e. m rows and n columns, is represented below:
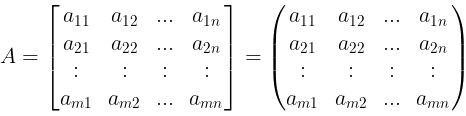 Abbreviated as: A = [aij]m × n, where 1 ≤ i ≤ m; 1 ≤ j ≤ n, i denotes the row and j denotes the column.
Abbreviated as: A = [aij]m × n, where 1 ≤ i ≤ m; 1 ≤ j ≤ n, i denotes the row and j denotes the column. - The number a11, a12, ….. etc., are known as the elements of matrix A, where aij belongs to the ith row and jth column and is called the (i, j)th element of the matrix A = [aij].
Type of Matrices
- Row Matrix: Matrix having one row i.e. matrix of order 1 × n. They are also known as row vectors.
Example: A = [a11 , a12, ...... a1n] - Column Matrix: Matrix having one column i.e. matrix of order m × 1. They are also known as column vectors.
Example: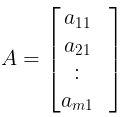
- Zero or Null Matrix: An m × n matrix all whose entries are zero. It is denoted as Om×n.
Example: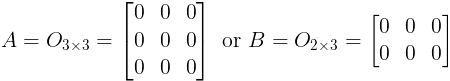
- Horizontal Matrix: A matrix of order m × n is a horizontal matrix if n > m.
Example: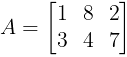
- Verical Matrix: A matrix of order m × n is a vertical matrix if m > n.
Example: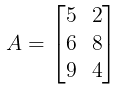
- Square Matrix: If number of rows is equal to number of column, then the matrix is a square matrix.
Example: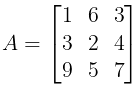
Note:
In a square matrix,
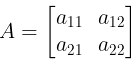
(a) The pair of elements aij & aji are called Conjugate Elements.
Example: a12 and a21(b) The elements a11, a22, a33, ...... ann are called Diagonal Elements. The line along which the diagonal elements lie is called the "Principal or Leading" diagonal.
(c) Sum of all the diagonal elements, i.e. Σ aii is known as trace of the matrix. It is denoted as tr(A).
- Diagonal Matrix: A square matrix in which all the elements are zero except the diagonal element. It is denoted as dia(d1, d2, ....., dn).
Example: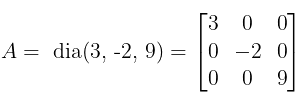
Note:
Min. number of zeros in a diagonal matrix of order n = n(n – 1)
- Scalar Matrix: A square matrix in which every non-diagonal element is zero and all diagonal elements are equal, is called a scalar matrix.
i.e. in scalar matrix, aij = 0, for i ≠ j and aij = k, for i = j
Example: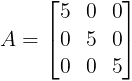
- Unit/Identity Matrix: A square matrix, in which every non-diagonal element is zero and every diagonal element is 1, is called, unit matrix or an identity matrix.
i.e. in scalar matrix, aij = 0, for i ≠ j and aij = 1, for i = j
Example: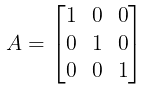
Equality of MatricesA = [aij] & B = [bij] will be equal, only if
- Both have the same order
- ai j = bi j for each pair of i & j
Operations on Matrices
For the Matrices,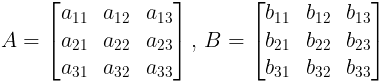
- Addition of Matrices: A + B = [ aij + bij], where A & B are of the same order.
i.e.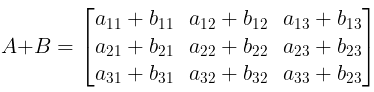
Properties:
(a) Addition of matrices is commutative i.e. A + B = B + A.
(b) Matrix addition is associative i.e. (A + B) + C = A + (B + C)
(c) Additive inverse. If A + B = O = B + A , then A and B are additive inverse of each other. - Multiplication of a Matrix by a Scalar: If a matrix is multiplied by a scalar quantity, then each element is multiplied by that quantity for the resulting matrix.
i.e.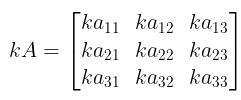 , where k is a scalar quantity.
, where k is a scalar quantity. - Multiplication of Matrices: Two matrices A, B can be multiplied to give resulting matrix AB, only if, no. of a column of A(prefactor) is equal to the no. of rows of B (post factor)
i.e. A is a matrix of order n x m and B is a matrix of order p x q, then AB exists only if m = p.
If m=p, order of AB = n x q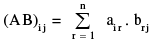
i.e.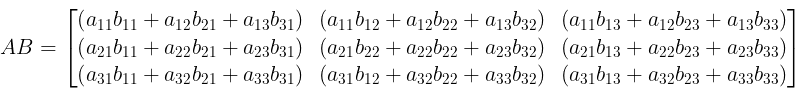
Properties:
(a) Matrix multiplication may or maynot be commutative i.e. AB may or may not be equal to BA.
(b) Matrix multiplication is Associative i.e. (A . B) . C = A . (B . C)
(c) Matrix multiplication is Distributive over Matrix Addition i.e. A(B+C) = AB + AC
(d) Cancellation Laws not necessary hold in case of matrix multiplication i.e. if AB = AC ⇒ B = C even if A ≠ 0.
(e) AB = 0 i.e., Null Matrix, does not necessarily imply that either A or B is a null matrix.
(f) Positive Integral Powers of a Square Matrix i.e. For a square matrix A , A2A = (AA) A = A (AA) = A3
Note:
- If A and B are two non-zero matrices such that AB = O then A and B are called the divisors of zero.
- If A and B are two matrices such that:
(i) AB = BA ⇒ A and B commute each other
(ii) AB = – BA ⇒ A and B anti commute each other- For a unit matrix I of any order , Im = I for all m ∈ N.
Illustration 1. Find the value of x and y, if 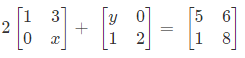
Ans. 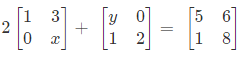
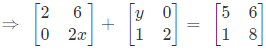
∴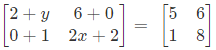
On equating the corresponding elements of L.H.S. and R.H.S.
A2 + y = 5 ⇒ y = 3
2x + 2 = 8 ⇒ 2x = 6 ⇒ x = 3
Thus, x = 3 and y = 3.
Illustration 2. If 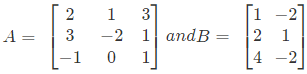 , find AB and BA if possible.
, find AB and BA if possible.
Ans. A is a 3 × 3 matrix and B is a 3 × 2 matrix, therefore, A and B are conformable for the product AB and it is of the order 3 × 2.
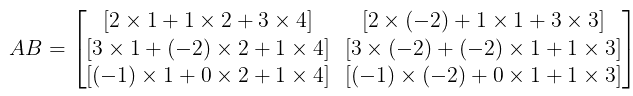
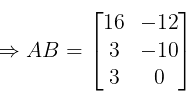
BA is not possible since the number of columns of B ≠ number of rows of A.
1 Matrix multiplication is commutative
2 Matrix multiplication is associative
3 Matrix multiplication is distributive over matrix addition
4 Cancellation laws hold true for matrix multiplication
Matrix Polynomial
- If f(x) = a0xn + a1xn – 1 + a2xn – 2 + ......... + anx0, then we define a matrix polynomial f(A) = a0An + a1An– 1 + a2An–2 + ..... + anIn where A is the given square matrix.
- If f (A) is the null matrix then A is called the zero or root of the polynomial f (x).
Special Matrices
(a) Idempotent Matrix: A square matrix is idempotent provided A2 = A
(b) Nilpotent Matrix: A square matrix is said to be nilpotent matrix of order m, m ∈ N , if Am = O, Am–1 ≠ O
(c) Periodic Matrix: A square matrix is periodic when it satisfies the relation AK+1 = A, for some positive integer K. The period of the matrix is the least value of K for which this holds true.
(d) Involutary Matrix: If A2 = I , the matrix is said to be an involutary matrix.
Note:
- For an idempotent matrix, An = A ∀ n > 2, n ∈ N.
- Period of an idempotent matrix is 1.
- For an involuntary Matrix, A = A–1.
Transpose of a Matrix
- The transpose of a matrix is obtained by changing its rows & columns.
- It is denoted as AT or A′.
- If a matrix be A = [ aij ] of order m x n, then AT or A′ = [ aji ] for 1 ≤ i ≤ n & 1 ≤ j ≤ m of order n × m
i.e.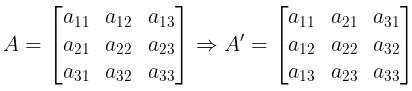
- Exxample:
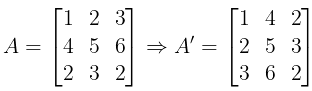
- Reversal law for transpose: (A1, A2, ...... An)T =
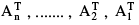
Properties of Transpose:
If AT & BT denote the transpose of A and B.
(a) (A ± B)T = AT ± BT ; note that A & B have the same order.
(b) (A B)T = BT AT A & B are conformable for matrix product AB.
(c) (AT)T = A
(d) (kA)T = k AT k is a scalar.
Symmetric & Skew-Symmetric Matrix
- A square matrix A = [ aij] is said to be, symmetric if , aij = aji ∀ i & j (conjugate elements are equal)
- A square matrix A = [ aij] is said to be, Skew-symmetric if , aij = -aji ∀ i & j (the pair of conjugate elements are additive inverse of each other)
Note:
(i) For symmetric matrix, A = AT
(ii) Max. number of distinct entries in a symmetric matrix of order n is
(iii) The digaonal elements of a skew symmetric matrix are all zero, but not the converse i.e. if digaonal elements are 0 doesn't mean matrix is skew symmetric.
Properties Of Symmetric & Skew Matrix
(a) A is symmetric, if AT = A and A is skew-symmetric, if AT = − A.
(b) A + AT is a symmetric matrix and A − AT is a skew symmetric matrix.
Consider (A + AT)T = AT + (AT)T = AT + A = A + AT. Thus, A + AT is symmetric.
Similarly, we can prove that A − AT is skew-symmetric.
(c) The sum of two symmetric matrices is a symmetric matrix and the sum of two skew-symmetric matrices is a skew-symmetric matrix.
(d) If A & B are symmetric matrices then,
(AB + BA) is a symmetric matrix and (AB − BA) is a skew-symmetric matrix.
(e) Every square matrix can be uniquely expressed as a sum of a symmetric and a skew-symmetric matrix.
i.e.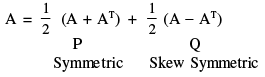
Adjoint of A Square Matrix
Let 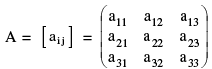 be a square matrix and let the matrix formed by the cofactors of [ai j ] in determinant A is =
be a square matrix and let the matrix formed by the cofactors of [ai j ] in determinant A is = 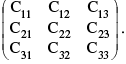 Then (adj A) =
Then (adj A) = 
Note: Co-factors of the elements of any matrix are obtained by eliminating all the elements of the same row and column and calculating the determinant of the remaining elements.
Theorem : A (adj. A) = (adj. A).A = |A| In, if A be a square matrix of order n.
Properties:
(i) | adj A | = | A |n – 1
(ii) adj (AB) = (adj B) (adj A)
(iii) adj(KA) = Kn–1 (adj A), K is a scalar
Illustration 3. If 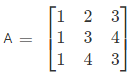 , find adj A.
, find adj A.
Ans. Each element of cofactor matrix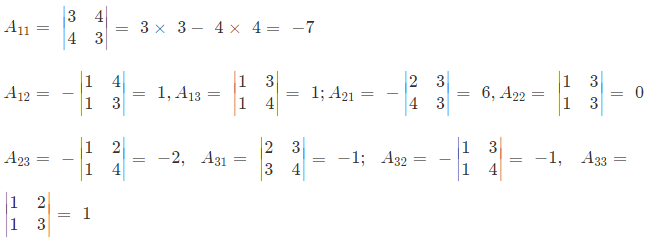
Cofactor matrix = 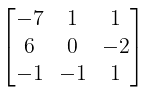
adj A = transpose of codaftor matrix = 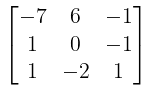
[Intext Question]
Elementary Transformation
Any one of the following operations on a matrix is called an elementary transformation.
- Interchanging any two rows (or columns), denoted by Ri↔Rj or Ci↔Cj

- Multiplication of the element of any row (or column) by a non-zero quantity and denoted by Ri → kRi or Ci → kCj
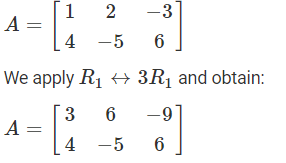
- Addition of constant multiple of the elements of any row to the corresponding element of any other row, denoted by Ri → Ri + kRj or Ci → Ci + kCj
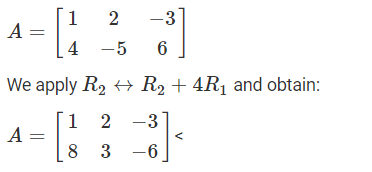
Inverse Of A Matrix (Reciprocal Matrix)
- A square matrix A said to be invertible (non singular) if there exists a matrix B such that, AB = I = BA. B is called the inverse (reciprocal) of A and is denoted by A−1.
- Thus A−1 = B ⇔ AB = I = BA.
- We have, A.(adj A) = |A| In
A−1 A (adj A) = A−1 In |Α|
In (adj A) = A−1 |A| In
∴ A−1 =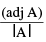
Imp. Theorem: If A & B are invertible matrices of the same order , then (AB)−1 = B−1A−1. This is reversal law for inverse
Note:
- The necessary and sufficient condition for a square matrix A to be invertible is that |A| ≠ 0.
- If A be an invertible matrix, then AT is also invertible & (AT)−1 = (A−1)T.
- If A is invertible,
(a) (A−1)−1 = A ;
(b) (Ak)−1 = (A−1)k = A–k, k ∈ N- If A is an Orthogonal Matrix. AAT = I = ATA
- A square matrix is said to be orthogonal if , A−1 = AT.
System of Equation & Criterian for Consistency Gauss - Jordan Method
a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3
We can write it in the form of matrix: 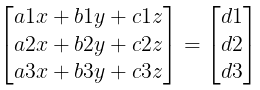
i.e. 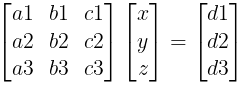
Let 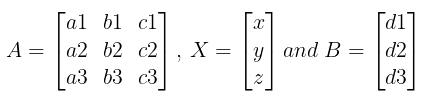
⇒ AX = B
⇒ A−1 A X = A−1 B
⇒ X = A−1 B = 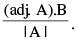
Note:
- If |A| ≠ 0, system is consistent having unique solution
- If |A| ≠ 0 & (adj A). B ≠ O (Null matrix), system is consistent having unique non − trivial solution.
- If |A| ≠ 0 & (adj A) . B = O (Null matrix) , system is consistent having trivial solution
- If |A| = 0, matrix method fails
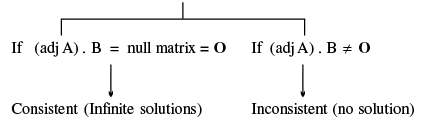
Illustration 4. Solve the following equation,
2x+y+2z=0, 2x-y+z=10, x+3y-z=5.
Ans. The given equation can be written in matrix form: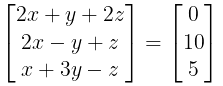
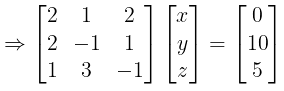
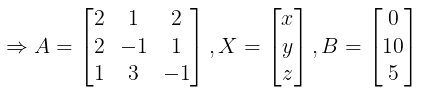
∵X = A−1 B = 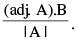
Therefore,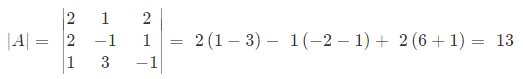
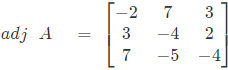
⇒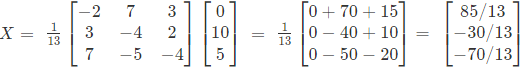
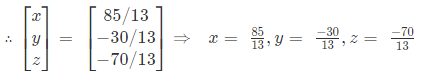
|
172 videos|503 docs|154 tests
|
FAQs on Overview: Matrices - Mathematics (Maths) for JEE Main & Advanced
| 1. What are the different types of matrices? |  |
| 2. How do we perform basic operations on matrices? |  |
| 3. What is a matrix polynomial, and how is it different from a regular polynomial? |  |
| 4. What is the significance of the transpose of a matrix? |  |
| 5. How can we find the inverse of a matrix, and what is its importance? |  |