Matrix-Match Type Questions: Miscellaneous (Sets, Relations, Statistics & Mathematica | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download

Each question contains statements given in two columns, which have to be matched. The statements in Column-I are labelled A, B, C and D, while the statements in Column-II are labelled p, q, r, s and t. Any given statement in Column-I can have correct matching with ONE OR MORE statement(s) in ColumnII. The appropriate bubbles corresponding to the answers to these questions have to be darkened as illustrated in the following example :

If the correct matches are A-p, s and t; B-q and r; C-p and q; and D-s then the correct darkening of bubbles will look like the given.

Q. Match the statements given in Column-I with the intervals/union of intervals given in Column-II.             (2011) 

Column-I                                                                                                                        Column-II

(A) The set 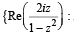: z is a complex number, |z| = 1 z ≠ ± 1}is                          (p) (-∞, - 1) ∪ (1,∞)

(B) The domain of the function f (x) =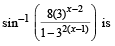                                        (q) (-∞, - 0) ∪ (0,∞)

(C) If 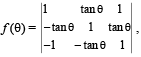 then the set                                    (r) [2, ∞)

                                                                                                                                        (s) (-∞, -1]U[1,∞) 

(D) If f (x) = x^3/2 (3x – 10), x ≥ 0 then f (x) is increasing in                                         (t) (-∞, 0]∪ [2,∞)

Ans. Sol. A → (s), B → (t), C → (r) D → (r)

et z = x + iy where and x² +  y² = 1 and x ≠ ± 1

Then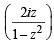 Re = Re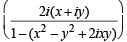

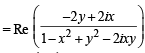
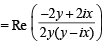
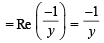
where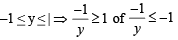

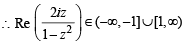 ∴ A  → s

(B) For the domain of f (x)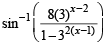 

We should have

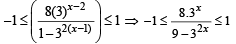
Let 3^x = t then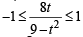

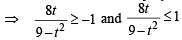
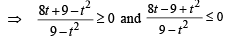
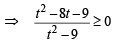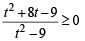
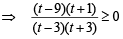and 

and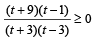 

Also t = 3x can not be – ve
∴ t ∈ (0, 3) ∪ [9,∞) and t ∈ (0,1] ∪ [3,∞)
Þ x ∈ (-∞,1) ∪ [2,∞) and x ∈ (-∞, 0] ∪ (1,∞)
Combining the two, we get x ∈ (-∞, 0] ∪ [2,∞)

∴ B → t

(C) 

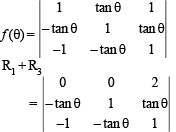
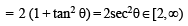
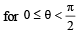
∴ C → r

(D) f (x) = x^3/2 (3x - 10),x ≥ 0

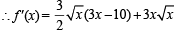
For f(x) to be increasing f'(x) ≥ 0

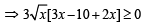
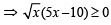 but x ≥ 0 ⇒ x ≥ 2

∴ f (x) is incresing on [2,∞) ∴ D → r.