Visualising Solid Shapes Class 7 Notes Maths
| Table of contents |

|
| Plane Figures and Solid Shapes |

|
| Faces, Edges and Vertices |

|
| Nets for Building 3D Shapes |

|
| Drawing Solids on a Flat Surface |

|
| Viewing Different Sections of a Solid |

|
Introduction
Have you ever looked around your classroom and noticed the different shapes all around you? From the cubes of your classroom blocks to the cylinders of soda cans, solid shapes are everywhere!
But what exactly are these solid shapes, and how do we visualize them?
This picture would be a 2D image because it has only two dimensions: length and width. It's like looking at a flat drawing of your pencil box on a piece of paper.
 2D Image
2D Image
In this chapter, we will explore the fascinating world of solid shapes, also known as 3D shapes. These shapes have depth, width, and height, making them much more interesting than flat shapes! You’ll learn how to identify, describe, and visualize shapes like cubes, spheres, cones, and pyramids.
 3D Image
3D Image
In simple terms, a 2D image is like a flat drawing, and a 3D image is like seeing the real object in front of you.
Plane Figures and Solid Shapes
- Visualizing solid shapes is an essential concept in mathematics, particularly in geometry.
- Solid shapes, also known as three-dimensional (3D) shapes, exist in physical space and have three dimensions: length, width, and height.
- Unlike two-dimensional shapes, such as squares and circles, which exist on a flat plane, solid shapes have volume and occupy space.
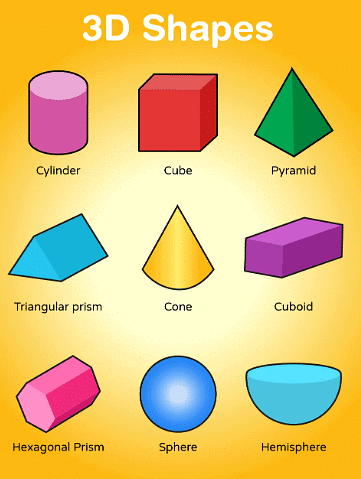
- Plane figures are flat or 2 -Dimension figures, they have no thickness.
For example: Squares, rectangles, circles, triangles etc. - Solid Shapes are 3-Dimensional shapes, and they occupy space and have volume.
For example: Cube, cuboid, sphere, cone, hemisphere etc.
Faces, Edges and Vertices
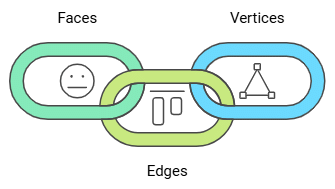
1. Faces
- A 3D shapes is not flat therefore it has 3 dimensions and these are faces, edges, and vertices.
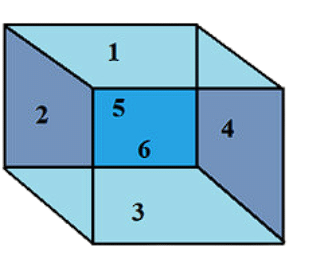
- Faces are simply the face of a 3D shape or the flat surface of the 3D shape.
For example: The number of faces of cube is 6
2. Edges
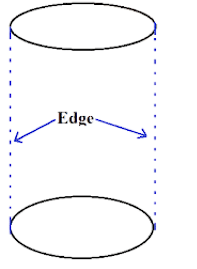
- Edges are the line segments which join one vertex to another vertex.
For example: Edges in a cylinder are 2 and are shown below.
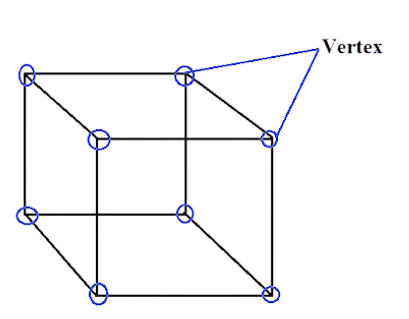
3. Vertices
- Points where two or more edges meet between faces is known vertices of any 3D shape or the corners of 3D shape.
For example: The cube has 8 vertices and is shown below
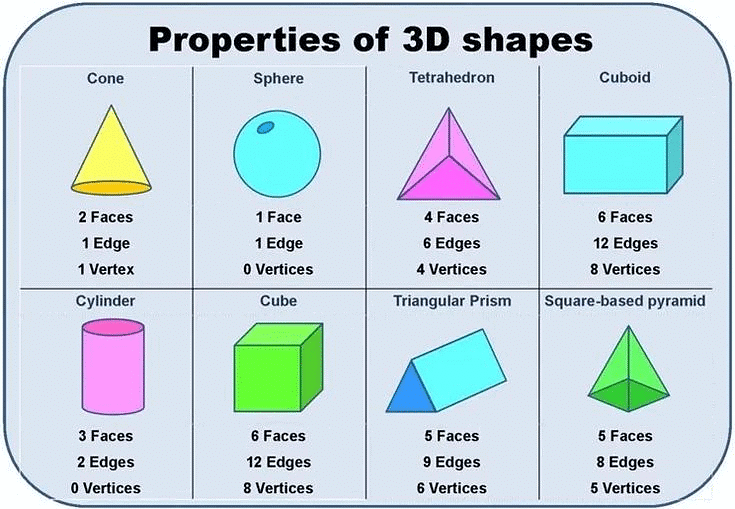
The table shows the number of the faces, edges and vertices of some shapes.
Nets for Building 3D Shapes
The net of a three-dimensional solid is a two-dimensional skeleton outline, which, when folded, results in the three-dimensional shape. Net is used for making 3D shapes.
- It is a basic skeleton outline in 2 -Dimensions i.e., it is flat 3-Dimensional shape which can be folded and joined together with the help of glue.
- Nets for building some shapes are shown below
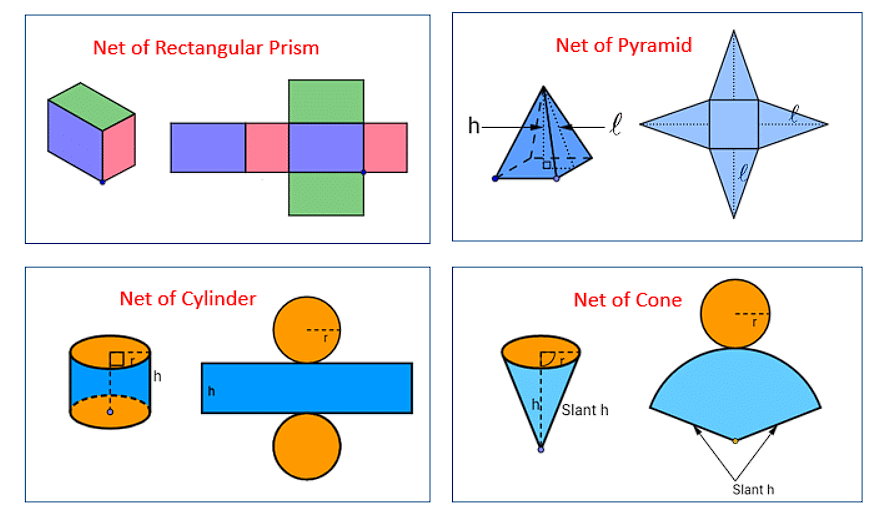
Nets of 3-D Shapes
Example to Practice: Match the following nets with appropriate solids.
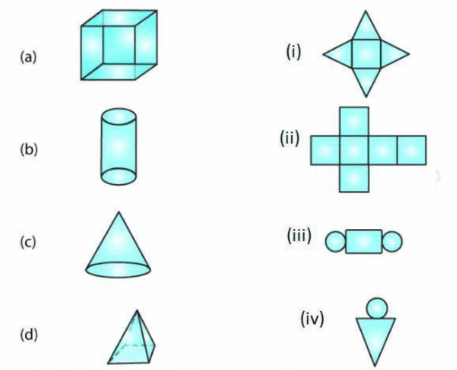
Solution:
(a) → (ii)
(b) → (iii)
(c) → (iv)
(d) → (i)
Drawing Solids on a Flat Surface
There are two techniques to create the illusion, of three-dimensionality when drawing solid shapes on a flat surface, such as paper.
1. Oblique Sketches
- These drawings show how 3D objects look from different angles.
- They're drawn by hand, without using any tools.
- They don't involve measuring the actual size of the 3D object.
- Below is a sketch of a cube drawn from an angle.

2. Isometric Sketches
- This method involves both drawing the 3D object and taking measurements.
- The drawings are done on special sheets called isometric sheets.
- Below is a sketch of a cube drawn using the isometric method, with the dotted sheet it's drawn on being called an isometric sheet.
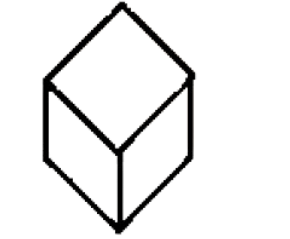
3. Visualising Solid Objects
- Visualising solid objects means understanding how 3D shapes look from different angles.
- It involves imagining the length, width, and height of an object, like a cube with its six visible faces.
- This skill is important in fields like architecture, engineering, and art, as it helps us comprehend the structure and design of objects.
 Visualising Solid Object
Visualising Solid Object
Viewing Different Sections of a Solid
There are many methods to view different sections of a solid:
(a) Slicing and Cutting: This method reveals the inside of a solid by slicing it into cross-sections.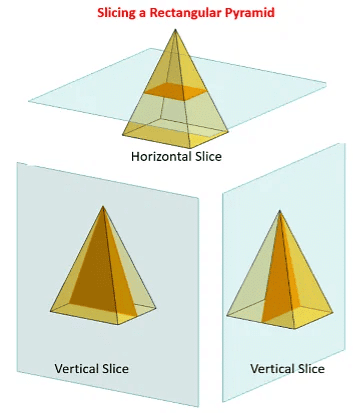
(b) Shadow Casting: This technique creates a two-dimensional representation of a three-dimensional object by casting its shadow. The resultant shape depends upon the side of the object where we throw the light.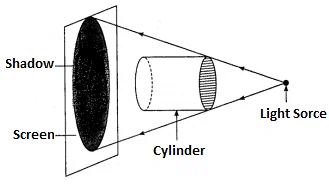 If we throw the light on the cylinder from its circular side then we will get the image of a circle.
If we throw the light on the cylinder from its circular side then we will get the image of a circle.
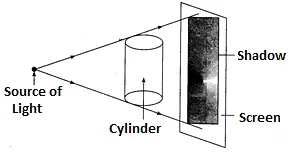
If we throw the light on the cylinder while it is on standing position then its shadow will be rectangular in shape.
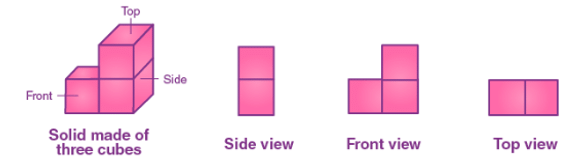
(c) Viewing from Different Angles: Observing a solid from various perspectives, such as front, side, and top views, offers valuable insights into its shape and structure.
Example: Different viewpoints of a building are illustrated below.
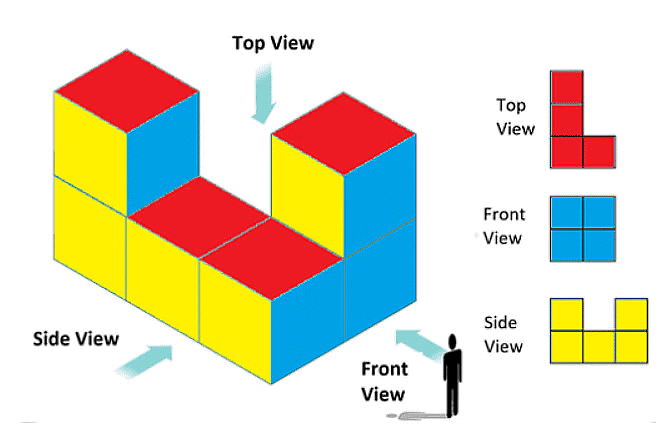
Remember, the skills you’ve developed in visualizing solid shapes are not just important in math; they also play a crucial role in fields like architecture, engineering, and art. So, keep observing the world around you and think about how these shapes connect to everything you see.
By building a strong foundation in understanding solid shapes, you're preparing yourself for more complex mathematical concepts in the future. So, let your curiosity guide you, and continue to explore the exciting shapes that make up our vibrant world!
|
76 videos|452 docs|39 tests
|
FAQs on Visualising Solid Shapes Class 7 Notes Maths
| 1. What are some examples of plane figures and solid shapes? |  |
| 2. What is the difference between faces, edges, and vertices of 3D shapes? |  |
| 3. How can nets be used to build 3D shapes? |  |
| 4. What is the purpose of drawing solids on a flat surface? |  |
| 5. How can different sections of a solid be viewed? |  |
















