NCERT Exemplar: Circles | Mathematics (Maths) Class 10 PDF Download
| Table of contents |

|
| Exercise 9.1 |

|
| Exercise 9.2 |

|
| Exercise 9.3 |

|
| Exercise 9.4 |

|
Exercise 9.1
Q.1. If radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is
(a) 3
(b) 6
(c) 9
(d) 1
Correct Answer is option (b)
Given, the radii of two concentric circles are 4 cm and 5 cm.
We have to find the length of each chord of one circle which is tangent to the other circle.
Consider two concentric circles.
OA = 4 cm
OB = 5 cm
If radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is
From the figure,
OA ⟂ BC
In triangle OAB,
The triangle OAB is a right triangle with A at right angle.
By pythagorean theorem,
OB² = OA² + AB²
(5)² = (4)² + AB²
25 = 16 + AB²
AB² = 25 - 16
AB² = 9
Taking square root,
AB = 3 cm
We know, BC = 2AB
So, BC = 2(3)
BC = 6 cm
Therefore, the length of each chord is 6 cm.
Q.2. In Fig. 9.3, if ∠AOB = 125°, then ∠COD is equal to
(a) 62.5°
(b) 45°
(c) 35°
(d) 55°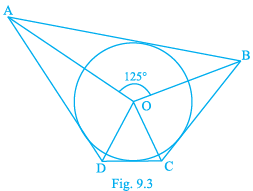
Correct Answer is option (d)
Given, ∠AOB = 125°
We have to find the measure of angle COD.
From the figure,
We observe that ABCD is a quadrilateral circumscribing the circle.
We know that, the opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the center of the circle.
The opposite sides are AB and CD
We have, ∠AOB + ∠COD = 180°
125° + ∠COD = 180°
∠COD = 180° - 125°
∠COD = 55°
Therefore, the measure of angle COD is 55°
Q.3. In Fig. 9.4, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at the point A, then ∠BAT is equal to
(a) 65°
(b) 60°
(c) 50°
(d) 40°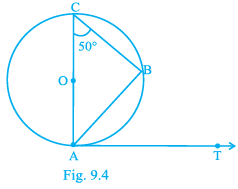
Correct Answer is option (c)
Given, AB is a chord of the circle.
AOC is the diameter of the circle.
Also, ∠ACB = 50°
AT is the tangent of the circle.
We have to find the measure of the angle BAT.
We know that the angle in a semicircle is a right angle.
So, ∠CBA = 90°
We know that the sum of all three interior angles of a triangle is always equal to 180°
In triangle AOB,
∠CAB + ∠CBA + ∠ACB = 180°
∠CAB + 90° + 50° = 180°
∠CAB + 140° = 180°
∠CAB = 180° - 140°
∠CAB = 40° ------------------- (1)
We know that radius of a circle is perpendicular to the tangent at the point of contact.
From the figure,
OA ⟂ OT
So, ∠CAB + ∠BAT = 90°
Substitute (1) in the above expression,
40° + ∠BAT = 90°
∠BAT = 90° - 40°
∠BAT = 50°
Therefore, the measure of the angle BAT is 50°
Q.4. From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is
(a) 60 cm2
(b) 65 cm2
(c) 30 cm 2
(d) 32.5 cm2
Correct Answer is option (a)
Given, P is a point at a distance of 13 cm from the centre O of a circle of radius 5 cm.
PQ and PR are the tangents of the circle.
We have to find the area of the quadrilateral.From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR isFrom the figure,OQ = OR = radius.We know that the radius of a circle is perpendicular to the tangent at the point of contact.So, ∠PQO = 90°∠PRO = 90°
Given, PO = 13 cm
Also, OP = OQ = 5 cm
In triangle PQO,
PQO is a right triangle with Q at right angle.
By pythagorean theorem,
(hypotenuse)² = (base)² + (height)²
(13)² = PQ² + (5)²
169 = PQ² + 25
PQ² = 169 - 25
PQ² = 144
Taking square root,
PQ = 12 cm
We know that the tangents through an external point to a circle are equal.
i.e., PQ = PR
So, PR = 12 cm
From the figure,
Area of quadrilateral PQRS = area of △POQ + area of △POR
In general, area of triangle = 1/2 × base × height
Area of △POQ = 1/2 × 5 × 12 = 60/2 = 30 cm²
Area of △POR = 1/2 × 5 × 12 = 60/2 = 30 cm²
Area of quadrilateral = 30 + 30 = 60 cm²
Therefore, the area of quadrilateral PQRS is 60 cm²
Q.5. At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is
(a) 4 cm
(b) 5 cm
(c) 6 cm
(d) 8 cm
Correct Answer is option (d)
Given, AB is the diameter of a circle
Radius of the circle is 5 cm
At one end A of the circle, tangent XAY is drawn.
We have to find the length of the chord CD parallel to XY and at a distance 8 cm from A.At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A isFrom the figure,XAY is the tangent of the circleCD is the chordThe distance of chord CD from A, AE = 8 cmRadius, AO = OC = 5 cm
We know that AE = AO + OE
8 = 5 + OE
OE = 8 - 5
OE = 3 cm
We observe that OE is perpendicular to the chord CD.
So, ∠ OEC = 90°
We know that the perpendicular drawn from the centre to the chord bisects the chord.
i.e., CE = DE
In triangle OED,
OED is a right triangle with right angle at E.
By pythagorean theorem,
OC² = OE² + CE²
(5)² = (3)² + CE²
CE² = 25 - 9
CE² = 16
Taking square root,
CE = 4 cm
Length of the chord CE = 2(CE)
= 2(4)
= 8 cm
Therefore, the length of the chord is 8 cm.
Q.6. In Fig. 9.5, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to
(a) 4 cm
(b) 2 cm
(c) 2√3 cm
(d) 4√3 cm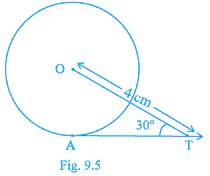
Correct Answer is option (c)
Given, AT is a tangent to the circle with centre O
The length of OT is 4 cm
Also, ∠OTA = 30°
We have to find the length of AT.
Join O and A.
OA will be the radius of the circle.
We know that radius of a circle is perpendicular to the tangent at the point of contact.
So, ∠OAT = 90°
In triangle AOT,
AOT is a right triangle with A at right angle.
By pythagorean theorem,
cos 30° = AT/OT
By using trigonometric ratios of angles,
cos 30° = √3/2
So, √3/2 = AT/4
On cross multiplication,
4√3/2 = AT
AT = 2√3 cm
Therefore, the measure of AT is 2√3 cm.
Q.7. In Fig. 9.6, if O is the centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to
(a) 100°
(b) 80°
(c) 90°
(d) 75°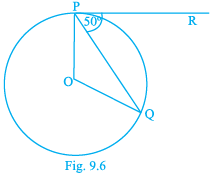
Correct Answer is option (a)
Given, O is the centre of a circle.
PQ is a chord
PR is a tangent at P which makes an angle of 50° with PQ.
We have to find the measure of angle POQ.
We know that the radius of a circle is perpendicular to the tangent at the point of contact.
i.e., ∠OPR = 90°
Given, ∠RPQ = 50°
We know that ∠OPR = ∠OPQ + ∠RPQ
90° = ∠OPQ + 50°
∠OPQ = 90° - 50°
∠OPQ = 40°
We know that if the opposite sides are equal then the opposite angles are equal.
From the figure,
OP = OQ = Radius
So, ∠OPQ = ∠OQP = 40°
In triangle POQ,
We know that the sum of all three interior angles of a triangle is always equal to 180°
∠OPQ + ∠OQP + ∠POQ = 180°
40° + 40° + ∠POQ = 180°
80° + ∠POQ = 180°
∠POQ = 180° - 80°
Therefore, ∠POQ = 100°
Q.8. In Fig. 9.7, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to
(a) 25°
(b) 30°
(c) 40°
(d) 50°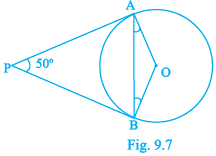
Correct Answer is option (a)
Given, PA and PB are tangents to the circle with centre O.
Also, ∠APB = 50°
We have to find the measure of angle OAB.
We know that the tangents through an external point to a circle are equal.
So, tangents PA = PB
In triangle PAB,
Since, PA = PB, PAB is an isosceles triangle.
In an isosceles triangle, two sides and two angles are equal.
i.e., PA = PB
Also, ∠PAB = ∠PBA —------------------ (1)
We know that the sum of three interior angles of a triangle is always equal to 180°
Now, ∠APB + ∠PAB + ∠PBA = 180°
From (1),
50° + ∠PAB + ∠PAB = 180°
2∠PAB = 180° - 50°
2∠PAB = 130°
∠PAB = 130°/2
∠PAB = 65°
since ∠PAB = ∠PBA, ∠PBA = 65°
We know that the radius of a circle is perpendicular to the tangent at the point of contact.
So, ∠PAO = ∠PBO = 90°
From the figure,
∠PAO = ∠PAB + ∠OAB
90° = 65° + ∠OAB
∠OAB = 90° - 65°
∠OAB = 25°
Therefore, the measure of the angle OAB is 25°
Q.9. If two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm, then length of each tangent is equal to
(a) 3√3/2 cm
(b) 6 cm
(c) 3 cm
(d) 3√3 cm
Correct Answer is option (d)
Given, two tangents are drawn to a circle of radius 3 cm, inclined at an angle of 60°
We have to find the length of each tangent.From the figure,
Let PA and PC be the tangents drawn to a circle
PA and PC inclined at 60°
So, ∠APC = 60°
We know that the tangents through an external point to a circle are equal.
So, PA = PC
In triangle OAP and triangle OCP,
PA = PC
OA = OC = radius of circle
OP = OP = common side
By SSS criterion, triangles OAP and OCP are similar,
We know that the radius of a circle is perpendicular to the tangent at the point of contact.
So, ∠OAP = ∠OCP = 90°
Since OA = OC = radius
∠OAP = ∠OCP
∠APC = ∠OAP + ∠OCP
So, 2∠OAP = 60°
∠OAP = 60°/2
∠OAP = 30°
In triangle OAP,
OAP is a right triangle with A at right angle.
tan 30° = OA/AP
By trigonometric ratio of angles,
tan 30° = 1/√3
So, 1/√3 = 3/AP
AP = 3√3 cm
We know, AP = CP = 3√3 cm
Therefore, the length of each tangent is 3√3 cm.
Q.10. In Fig. 9.8, if PQR is the tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to
(a) 20°
(b) 40°
(c) 35°
(d) 45°
Correct Answer is option (b)
Given, PQR is the tangent at Q to a circle whose centre is O.
AB is a chord parallel to PR.
Also, ∠BQR = 70°
We have to find the measure of angle AQB.
We know that the radius of a circle is perpendicular to the tangent at the point of contact.
So, ∠OQR = ∠OQP = 90°
From the figure,
∠OQR = ∠OQB + ∠BQR
90° = ∠OQB + 70°
∠OQB = 90° - 70°
∠OQB = 20°
Let the line from O meet AB at C.
Considering triangles AQM and BQM,
We know that the perpendicular from the centre of the circle to the chord bisects the chord.
So, AC = BC
∠QMA = ∠QMB = 90°
QM = QM = common side
By SAS criterion, the triangles AQM and BQM are similar.
So, ∠MQA = ∠MQB = 20°
From the figure,
∠AQB = ∠MQA + ∠MQB
∠AQB = 20° + 20°
∠AQB = 40°
Therefore, the measure of the angle AQB is 40°
Exercise 9.2
Q.1. If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°. Write ‘True’ or ‘False’ and justify your answer.
False
Let us consider the figure in which a circle with centre O and AB a chord with ∠AOB = 60°If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°. Write ‘True’ or ‘False’ and justify your answerAs tangent to any point on the circle is perpendicular to the radius through the point of contact,OA ⏊ AC and OB ⏊ CB∠OBC = ∠OAC = 90° …(1)Using angle sum property of quadrilateral in Quadrilateral AOBC,
∠OBC + ∠OAC + ∠AOB + ∠ACB = 360°
Substituting the values
90° + 90° + 60° + ∠ACB = 360°
So we get
∠ACB = 120°
Angle between two tangents is 120°.
Therefore, the statement is false.
Q.2. The length of tangent from an external point on a circle is always greater than the radius of the circle. Write ‘True’ or ‘False’ and justify your answer.
False
The length of tangent from an external point on a circle is always greater than the radius of the circle. Write ‘True’ or ‘False’ and justify your answer
Let P be a point external to the circle away from O
Construct a tangent PA on the circle
PA > r
Now, let us consider a point P1 on the tangent AP near to contact point A of tangent
PA, P1A < AO
The length of tangent PA and P1A are greater and smaller than the radius OA
So the length of tangent may or may not be greater than the radius
Therefore, the statement is false.
Q.3. The length of tangent from an external point P on a circle with centre O is always less than OP. Write ‘True’ or ‘False’ and justify your answer.
True
Let us consider the figureThe length of tangent from an external point P on a circle with centre O is always less than OP. Write ‘True’ or ‘False’ and justify your answerPT is the tangent from the external point PJoin OTOT ⏊ PTWe know thatA tangent at any point on the circle is perpendicular to the radius through the point of contact.
OPT is a right-angled triangle formed.
In a right angled triangle, the hypotenuse is always greater than any of the two sides of the triangle.
OP > PT or PT < OP
The length of tangent from an external point on a circle is always less than the radius of the circle.
Therefore, the statement is true.
Q.4. The angle between two tangents to a circle may be 0°. Write ‘True’ or ‘False’ and justify your answer.
True
It might be possible if both tangent lines coincide or parallel to each other. The angle between two tangents to a circle may be 0°. Write ‘True’ or ‘False’ and justify your answer. Therefore, the statement is true.
The angle between two tangents to a circle may be 0°. Write ‘True’ or ‘False’ and justify your answer. Therefore, the statement is true.
Q.5. If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = a√2. Write ‘True’ or ‘False’ and justify your answer.
True
Consider a circle with centre O and tangents PT and PR and angle between them is 90° and radius of the circle is aIn △OTP and △ORPTO = OR [radii of same circle]OP = OP [common]TP = PR [tangents through an external point to a circle are equal]△OTP ≅ △ORP [By SSS Criterion ]
∠TPO = ∠OPR [c.p.c.t] --- (1)
Given, ∠TPR = 90°
∠TPO + ∠OPR = 90°
∠TPO + ∠TPO = 90° [From 1]
∠TPO = 45°
As tangent at any point on the circle is perpendicular to the radius through point of contact
OT ⏊ TP
∠OTP = 90°
△POT is a right-angled triangle
We know that,
sin θ = perpendicular/hypotenuse
sin ∠TPO = OT/OP = a/OP
sin 45° = a/OP
1/√2 = a/OP
OP = a√2
Therefore, it is true.
Q.6. If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = a√3. Write ‘True’ or ‘False’ and justify your answer.
False
Consider a circle with center O and tangents PT and PR, angle between them is 60° and radius of circle is a.In △OTP and △ORPTO = OR [radii of same circle]OP = OP [common]TP = PR [tangents through an external point to a circle are equal]△OTP ≅ △ORP [By SSS Criterion ]∠TPO = ∠OPR [c.p.c.t] --- [1]Given, ∠TPR = 60°
∠TPO + ∠OPR = 60°
∠TPO + ∠TPO = 60° [From equation 1]
∠TPO = 30°
As tangent at any point on the circle is perpendicular to the radius through point of contact
OT ⏊ TP
∠OTP = 90°
△POT is a right-angled triangle
We know that,
sin θ = perpendicular/hypotenuse
sin ∠TPO = OT/OP = a/OP
sin 30° = a/OP
1/2 = a/OP
OP = 2a
Therefore, the statement is false.
Q.7. The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC. Write ‘True’ or ‘False’ and justify your answer.
True
Consider a circle in which EF is a tangent passing through point A on the circle and ABC is an isosceles triangle in the circle, in which AB = ACTo Prove: EF || BC
Construction: Join OA , OB and OC
Proof:
AB = AC [Given]
Angles opposite to equal sides are equal
∠ACB = ∠ABC --- [1]
Since we know that the angle between the chord and the tangent is equal to the angle made by the chord in the alternate segment
Therefore,
∠EAB = ∠ACB --- [2]
From [1] and [2]
∠EAB = ∠ACB
Two lines are parallel if their alternate interior angles are equal
EF || BC
Therefore, the statement is true.
Q.8. If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ. Write ‘True’ or ‘False’ and justify your answer.
False
Consider S1, S2, S3, …., Sn be n circles with centers C1, C2, C3, …, Cn.
PQ is a common tangent to all the circles at point A that is common to all circles.
We know that, tangent at any point on the circle is perpendicular to the radius through point of contact
We have,
C1A ⏊ PQ
C2A ⏊ PQ
C3A ⏊ PQ
CnA ⏊ PQ
Here, C1 C2 C3 … Cn lie on the perpendicular line to PQ but not on the perpendicular bisector as PA may or may not be equal to AQ.
Therefore, the statement is false.
Q.9. If a number of circles pass through the end points P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ. Write ‘True’ or ‘False’ and justify your answer.
True
Draw a line segment PQ and S1 S2 S3 …. Sn are n circles with center C1 C2 C3 … Cn passing through P and Q
Sp PQ will be a chord to a circle or the diameter (It is possible once when diameter length is equal to the length of PQ)
If PQ is diameter then the center lies on the half of diameter i.e. on the perpendicular bisector of PQ.
If PQ is a chord then perpendicular from the center to the chord of circle bisect the chord
It implies that the center lies on the perpendicular bisector of the chord.
For each circle the center lies on the perpendicular bisector of PQ.
Therefore, the statement is true.
Q.10. AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD. Write ‘True’ or ‘False’ and justify your answer.
True
First join OC
∠BCD = ∠BAC = 30° (angles in alternate segment)
Arc BC subtends ∠DOC at the centre of the circle and ∠BAC at the remaining part of the circle.
∠BOC = 2 ∠BAC = 2 × 30° = 60°
In triangle OCD
∠BOC = ∠DOC = 60°
∠OCD = 90°
OC is perpendicular to CD
∠DOC + ∠ODC = 90°
60° + ∠ODC = 90°
∠ODC = 90° - 60° = 30°
In triangle BCD
∠ODC = ∠BDC = ∠BCD = 30°
So BC = BD
Therefore, the statement is true.
Exercise 9.3
Q.1. Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
Given, two concentric circles with centre O
Radius of the outer circle = 5 cm
Chord AC is tangent to the inner circle.
The length of the chord, AC = 8 cm
We have to find the radius of the inner circle.
From the figure,
Let C1 be the inner circle
Let C2 be the outer circle with radius 5 cm.
Joining O to the chord AC which meets at D.
We know that the perpendicular drawn from the centre of a circle to the chord always bisects the chord.
So, OD ⟂ AC
Also, AD = DC = AC/2
AC/2 = 8/2 = 4 cm
So, AD = DC = 4 cm
Considering triangle OAD,
ODA is a right triangle with D at right angle.
By pythagoras theorem,
AO² = AD² + OD²
OD = radius of inner circle
OA = radius of outer circle = 5 cm
AD = 4 cm
So, (5)² = (4)² + OD²
25 = 16 + OD²
OD² = 25 - 16
OD² = 9
Taking square root,
OD = 3 cm
Therefore, the radius of the inner circle is 3 cm.
Q.2. Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
Given, PQ and PR are the two tangents drawn from an external point to a circle with centre O.
We have to prove that QORP is a cyclic quadrilateral.Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateralFrom the figure,O is the centre of the circleOR and OQ = radius of the circlePR and PQ are the two tangents to the circle from an external point P.
We know that the radius of a circle is perpendicular to the tangent at the point of contact.
So, OR ⟂ PR and OQ ⟂ PQ
∠ORP = ∠OQP = 90°
We know that the sum of all interior angles in a quadrilateral is always equal to 360°
Considering quadrilateral PQOR,
∠OQP + ∠QOR + ∠ORP + ∠RPQ = 360°
90° + ∠QOR + 90° + ∠RPQ = 360°
180° + ∠QOR + ∠RPQ = 360°
∠QOR + ∠RPQ = 360° - 180°
So, ∠O + ∠P = 180°
Here opposite angles are supplementary.
Therefore, PQOR is a cyclic quadrilateral.
Q.3. If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BC
Given, BC and BD are the tangents drawn from an external point B of a circle with centre O.
Also, ∠DBC = 120°We have to prove that BC + BD = BO, i.e., BO = 2BC.If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BCWe know that the radius of the circle is perpendicular to the tangent at the point of contact.So, OC ⟂ BC and OD ⟂ BDConsidering triangles OCB and ODB,
OB = OB = common side
We know that the tangents drawn through an external point to a circle are equal.
So, BC = BD
Also, ∠OCB = ∠ODB = 90°
By RHS criteria, the triangles OCB and ODB are similar.
By corresponding parts of congruent triangles,
The angles ∠OBC and ∠OBD are equal.
So, ∠OBC = ∠OBD = 60°
Considering triangle OCB,
OCB is a right triangle with C at right angle.
By pythagorean theorem,
cos 60° = BC/OB
By trigonometric ratio of angles,
cos 60° = 1/2
So, 1/2 = BC/OB
OB = 2BC
Therefore, it is proved that OB = 2BC.
Q.4. Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
Given, the centre of a circle touches two intersecting lines
We have to prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines
Consider a circle with centre O.
PR and PQ are the tangents drawn through an external point P to the circle.
Join OR and OQ which represents the radius of the circle.
We know that the radius of the circle is perpendicular to the tangent at the point of contact.
So, OR ⟂ PR and OQ ⟂ PQ
Considering triangles PRO and PQO.
PO = PO = common side
OR = OQ = radius
∠PQO = ∠PRO = 90°
By RHS criterion, the triangles PQO and PRO are similar.
By corresponding parts of congruent triangles,
The angles ∠RPO and ∠QPO are equal.
So, ∠RPO = ∠QPO
This implies that O lies on the angle bisector of PR and PQ.
Therefore, it is proved that the centre of the circle lies on the angle bisector of PR and PQ.
Q.5. In Fig. 9.13, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.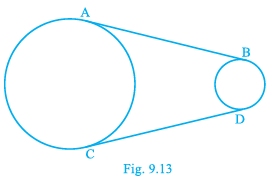
Given, AB and CD are the common tangents to two circles of unequal radii.
We have to prove that AB = CD.Extend AB and CD such that it intersects at P.
We know that the tangents to a circle through an external point are equal.
Considering smaller circle,
The tangents are PB and PD
So, PB = PD ---------- (1)
Considering the larger circle,
The tangents are PA and PC
So, PA = PC ---------- (2)
Subtracting (1) and (2),
PA - PB = PC - PD
From the figure,
PA - PB = AB
PC - PD = CD
Therefore, AB = CD
Q.6. In Fig. 9.13, AB and CD are common tangents to two circles. If the radii of the two circles are equal, prove that AB = CD.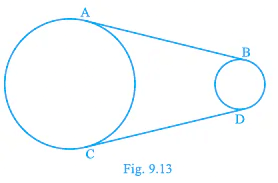
Given, AB and CD are the common tangents of two circles with equal radii.
We have to prove that AB = CDWe know that the radius of the circle is perpendicular to the tangent at the point of contact.So, OA ⟂ AB, O'D ⟂ CD, O'B ⟂ AB and OC ⟂ CDAlso, ∠OAB = ∠O'BA = ∠OCD = ∠ODC = 90°From the figure,We observe that AC and BD are straight lines
ABCD represents a quadrilateral
∠A = ∠B = ∠C= ∠D = 90°
So, ABCD is a rectangle.
We know that the opposite sides are equal in a rectangle.
i.e., AB = CD and AC = BD
Therefore, it is proved that AB = CD
Q.7. In Fig. 9.14, common tangents AB and CD to two circles intersect at E. Prove that AB = CD.
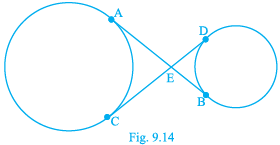
Given, AB and CD are common tangents to two circles.
The tangents intersect at E.
we have to prove that AB = CD
From the figure,
E is the external point
The tangents drawn through external point E are EA, EC, EB and ED.
We know that the tangents drawn through an external point to a circle are equal.
So, EA = EC ---------------- (1)
EB = ED ---------------------- (2)
Adding (1) and (2),
EA + EB = EC + ED
From the figure,
AB = EA + EB
CD = EC + ED
So, AB = CD
Therefore, it is proved that AB = CD.
Q.8. A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
Given, a chord PQ of a circle is parallel to the tangent drawn at a point R of the circle.
We have to prove that R bisects the arc PRQ.From the figure,
MN is the tangent to the circle at the point R.
PQ is the chord
Given, PQ || MN
The alternate interior angles are equal.
i.e., ∠MRP = ∠RPQ
∠1 = ∠2 ------------------ (a)
We know that the angle between the tangent and the chord of a circle is equal to the angle made by the chord in the alternate segment.
So, ∠MRP = ∠RQP
∠1 = ∠3 ----------------- (b)
From (a) and (b),
∠2 = ∠3
∠MRP = ∠RQP
We know that the sides equal to the opposite angles are equal.
So, PR = QR.
This implies that R bisect PQ.
Therefore, R bisects the arc PRQ.
Q.9. Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
We have to prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
From the figure,
O is the centre of the circle.
AB is a chord of the circle.
PA and PB are the tangents drawn at the ends of a chord of the circle.
The tangents intersect at P.
Join OA and OB.
OA = OB = radius of the circle.
Considering triangle OAB,
OA = OB = radius of the circle.
Since the two sides of the triangle are equal, OAB is an isosceles triangle.
We know that the angles opposite to the equal sides of a triangle are equal.
So, ∠OAB = ∠OBA
i.e., ∠1 = ∠2 ------------- (1)
We know that the radius of the circle is perpendicular to the tangent at the point of contact.
So, OA ⟂ PA and OB ⟂ PB
∠OAP = ∠OBP = 90°
i.e., ∠2 + ∠3 = ∠1 + ∠4 -------------- (2)
Substituting (1) in (2),
∠1 + ∠3 = ∠1 + ∠4
∠1 + ∠3 - ∠1 = ∠4
∠3 = ∠4
Therefore, ∠PAB = ∠PBA.
Q.10. Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
Given, AB is the diameter of a circle.
AB bisects all those chords which are parallel to the tangent at the point A.From the figure,
AB is the diameter of the circle.
CD is the chord of the circle.
MN is the tangent to the circle at the point A.
OA = OB = OC = OD = radius of the circle.
We know that the radius of a circle is perpendicular to the tangent at the point of contact.
So, OA ⟂ MN
Also, ∠MAO = ∠NAO = 90°
The corresponding angles are equal.
∠CEO = ∠MAO
So, ∠CEO = 90°
We know that the perpendicular drawn from the centre of the circle to the chord always bisects the chord.
It implies that OE bisects CD.
Therefore, diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
Exercise 9.4
Q.1. If a hexagon ABCDEF circumscribes a circle, prove that AB + CD + EF = BC + DE + FA.
Given, a hexagon ABCDEF circumscribe a circle
We have to prove that AB + CD + EF = BC + DE + FA
We know that the tangents to a circle through an external point are equal.From the figure,
AR and AM are the tangent to the circle through an point A
So, AM = AR ------ (1)
Similarly,
The tangents through point B
BM = BN ------- (2)
The tangents through point C
CO = CN -------- (3)
The tangents through point D
DO = DP ------- (4)
The tangents through point E
EQ = EP ------- (5)
The tangents through point F
FQ = FR ------- (6)
Adding (1) to (6),
AM + BM + CO + DO + EQ + FQ = AR + BN + CN + DP + EP + FR
On rearranging,
(AM + BM) + (CO + DO) + (EQ + FQ) = (AR + FR) + (BN + CN) + (EP + DP)
From the figure,
AM + BM = AB
CO + DO = CD
EQ + FQ = EF
AR + FR = AF
BN + CN = BC
EP + DP = ED
So, AB + CD + EF = AF + BC + ED
Therefore, AB + CD + EF = BC + DE + FA
Q.2. Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s – b.
Given, s denotes the semiperimeter of a triangle ABC.
The sides of triangle BC = a, CA = b and AB = c.
A circle touches the sides BC, CA, AB at D, E and F
We have to prove that BD = s - bSemiperimeter of atriangle is half the sum of the sides of the triangle.
Semiperimeter of a triangle is given by
s = (a + b + c)/2
We know that the tangents to a circle through an external point are equal.
The tangents through point A are AF and AE
So, AF = AE ------ (1)
The tangents through point B are BF and BD
So, BF = BD - ------ (2)
The tangents through point C are CD and CE
So, CD = CD ----- (3)
Semiperimeter, s = (AB + BC + CA)/2
2s = AB + BC + CA
From the figure,
AB = AF + FB
BC = BD + DC
CA = CE + EA
2s = AF + FB + BD + DC + CE + EA
From (1), (2) and (3),
2s = AE + AE + CE + CE + BD + BD
2s = 2AE + 2CE + 2B
2s = 2(AE + CE + BD)
Cancelling out common term,
s = AE + CE + BD
From the figure,
AC = AE + CE
So, s = AC + BD
We know AC = b
s = b + BD
BD = s - b
Therefore, it is proven that BD = s - b
Q.3. From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the the perimeter of the triangle PCD.
Given, PA and PB are the two tangents drawn to a circle with centre O though an external point P.
At point E on the circle the tangent is drawn which intersects PA and PB at C and D.
Given, PA = 10 cm
We have to find the perimeter of the triangle PCD.We know that the tangents drawn to a circle through an external point are equal.
From the figure,
The tangents drawn through point P are PA and PB
So, PA = PB -------------- (1)
The tangents to the circle through C are CA and CE
So, CA = CE -------------- (2)
The tangents to the circle through D are DB = DE
So, DB = DE -------------- (3)
Considering triangle PCD,
Perimeter = PC + PD + CD
From the figure,
CD = CE + DE
So, perimeter = PC + PD + CE + DE
From (2) and (3),
Perimeter = PC + PD + CA + DB
On rearranging,
Perimeter = PC + CA + PD + DB
From the figure,
PC + CA = PA
PD + DB = PB
By (1), PA = PB
So, perimeter = PA + PB
Perimeter = PA + PA
= 2PA
Given, PA = 10 cm
So, 2PA = 2(10)
= 20 cm
Therefore, the perimeter of the triangle PCD is 20 cm.
Q.4. If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in Fig. 9.17. Prove that ∠BAT = ∠ACB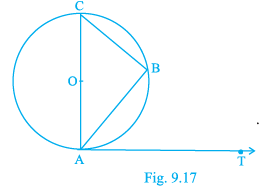
Given, AB is a chord of a circle with centre O.
AOC is a diameter of the circle
AT is the tangent at point A
We have to prove that ∠BAT = ∠ACB
We know that angle in a semicircle is always equal to 90°
So, ∠CBA = 90°
Considering triangle CBA,
We know that the sum of all three interior angles of a triangle is always equal to 180°
∠CBA + ∠BAC + ∠ACB = 180°
90° + ∠BAC + ∠ACB = 180°
∠BAC + ∠ACB = 180° - 90°
∠BAC + ∠ACB = 90°
∠ACB = 90° - ∠BAC ------- (1)
We know that the radius of the circle is perpendicular to the tangent at the point of contact.
So, OA ⟂ AT
∠OAT + ∠CAT = 90°
From the figure,
∠CAT = ∠BAT + ∠BAC
90° = ∠BAT + ∠BAC
∠BAT = 90° - ∠CAB ----- (2)
Comparing (1) and (2),
Since RHS are same
∠ACB = ∠BAT
Therefore, it is proved that ∠ACB = ∠BAT
Q.5. Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of the common chord PQ.
Given, two circles with centres O and O' have radii 3 cm and 4 cm.
Two circles intersect at two points P and Q.
OP and O’P are the tangents to the two circles.
We have to find the length of the common chord PQ.We know that the radius of a circle is perpendicular to the tangent at the point of contact.
So, ∠OPO’ = 90°
Considering triangle OPO’,
OPO’ is a right triangle with P at right angle.
By pythagoras theorem,
(OO’)² = (OP)² + (O’P)²
From the figure,
OP = radius of circle = 3 cm
O’P = radius of other circle = 4 cm
(OO’)² = (3)² + (4)²
(OO’)² = 9 + 16
(OO’)² = 25
Taking square root,
OO’ = 5 cm
Let ON = x cm
So, O’N = 5 - x cm
In triangle ONP,
By pythagoras theorem,
(OP)² = (ON)² + (PN)²
(3)² = (x)² + (PN)²
9 = x² + (PN)²
PN² = 9 - x² ---------- (1)
In triangle O’NP,
(O’P)² = (O’N)² + (PN)²
(4)² = (5 - x)² + PN²
PN² = 16 - (5 - x)²
By using algebraic identity,
(a - b)² = a² - 2ab + b²
PN² = 16 - (25 -10x + x²)
PN² = 16 - 25 + 10x - a²
PN² = -x² + 10x - 9 ---------- (2)
Comparing (1) and (2),
9 - x² = -x² + 10x - 9
9 = 10x - 9
10x = 9 + 9
10x = 18
x = 18/10
x = 1.8
Substitute the value of x in (1),
PN² = 9 - (1.8)²
PN² = 9 - 3.24
PN² = 5.76
Taking square root,
PN = 2.4 cm
We know, PQ = 2PN
PQ = 2(2.4)
PQ = 4.8 cm
Therefore, the length of the chord PQ is 4.8 cm
Q.6. In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
Given, ABC is a right triangle with B at right angle.
A circle is drawn with AB as diameter intersecting the hypotenuse AC at P.
We have to prove that the tangent to the circle at P bisects BC.We know that angle in a semicircle is always equal to 90°
So, ∠APB = 90°
A linear pair of angles is formed when two lines intersect.
By linear pair of angles,
∠BPC = 90°
So, ∠3 + ∠4 = 90° ----------- (1)
Given, ∠B = 90°
In triangle ABC,
We know that the sum of all three interior angles of a triangle is always equal to 180°
∠BAC + ∠ABC + ∠ACB = 180°
∠1 + 90° + ∠5 = 180°
∠1 + ∠5 = 180° - 90°
∠1 + ∠5 = 90° ---------- (2)
We know that the angle between the tangent and the chord of a circle is equal to the angle made by the chord in the alternate segment.
So, ∠1 = ∠3 ------------ (3)
Substitute (3) in (2),
∠3 + ∠5 = 90° ------- (4)
Comparing (1) and (4),
∠3 + ∠4 = ∠3 + ∠5
∠3 + ∠4 - ∠3 = ∠5
∠4 = ∠5
From the figure,
∠4 = ∠CPQ
∠5 = ∠PCQ
So, ∠CPQ = ∠PCQ
We know that the sides opposite to equal angles are equal.
QC = PQ ----------- (5)
We know that the tangents drawn through an external point to a circle are equal.
Now, PQ = BQ
From (5), BQ = QC
This implies that PQ bisects BC
Therefore, it is proved that the tangent to the circle at P bisects BC.
Q.7. In Fig. 9.18, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS. [Hint: Draw a line through Q and perpendicular to QP.]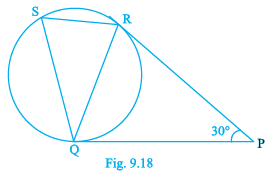
Given, PQ and PR are the tangents drawn to a circle.
Also, ∠RPQ = 30°
A chord RS is drawn parallel to the tangent PQ.
We have to find the measure of angle RQS.
We know that the tangents drawn through an external point to a circle are equal.
So, PQ = PR.
We know that the angles opposite to the equal sides are equal in a triangle.
So, ∠PRQ = ∠PQR --------------- (1)
Considering triangle PQR,
We know that the sum of all three interior angles of a triangle are equal.
∠PQR + ∠RPQ + ∠PRQ = 180°
∠PQR + 30° + ∠PRQ = 180°
∠PQR + ∠PRQ = 180° - 30°
∠PQR + ∠PRQ = 150°
From (1),
∠PQR + ∠PQR = 150°
2∠PQR = 150°
∠PQR = 150°/2
∠PQR = 75°
Since PQ = PR, ∠PQR = ∠PRQ = 75°
We know that the angle between the tangent and the chord of a circle is equal to the angle made by the chord in the alternate segment.
So, ∠PQR = ∠RSQ = 75° ---------- (2)
Since RS || PQ,
The alternate angles are equal.
i.e., ∠PQR = ∠QRS = 75° --------- (3)
Comparing (2) and (3),
∠RSQ = ∠QRS = 75°
We know that the sides opposite to equal angles are equal.
So, SQ = RQ
This implies QRS is an isosceles triangle.
In triangle QRS,
By angle sum property,
∠RSQ + ∠QRS + ∠RQS = 180°
75° + 75° + ∠RQS = 180°
150° + ∠RQS = 180°
∠RQS = 180° - 150°
Therefore, ∠RQS = 30°
Q.8. AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
Given, AB is a diameter of a circle with centre O
AC is a chord of a circle.
Also, ∠BAC = 30°
The tangent at C intersects extended AB at a point D.
We have to prove that BC = BD.By alternate segment theorem,
We know that the angle between the tangent and the chord of a circle is equal to the angle made by the chord in the alternate segment.
So, ∠BCD = ∠BAC
Given, ∠BAC = 30°
Then, ∠BCD = 30° --------- (1)
We know that the angle in a semicircle is always equal to 90°
∠ACB = 90°
In triangle ABC,
∠CAB + ∠CBA + ∠ACB = 180°
30° + ∠CBA + 90° = 180°
120° + ∠CBA = 180°
∠CBA = 180° - 120°
∠CBA = 60°
From the figure,
Linear pair of angles,
∠CBA + ∠CBD = 180°
60° + ∠CBD = 180°
∠CBD = 180° - 60°
∠CBD = 120°
Considering triangle CBD,
We know that the sum of all three interior angles of a triangle is always equal to 180°
∠CBD + ∠BCD + ∠BDC = 180°
120° + 30° + ∠BDC = 180°
150° + ∠BDC = 180°
∠BDC = 180° - 150°
∠BDC = 30° ----------- (2)
Comparing (1) and (2),
∠BCD = ∠BDC = 30°
We know that the sides opposite to equal angles are equal.
So, BC = BD
Therefore, it is proved that BC = BD
Q.9. Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
Given, a tangent is drawn at the midpoint of an arc of a circle.
We have to prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.From the figure,
Centre of the circle is O.
P is the midpoint of arc APB
PT is a tangent to a circle at P
We know that the radius of the circle is perpendicular to the tangent at the point of contact.
So, OP ⟂ PT
∠OPT = 90°
Since P is the midpoint of arc APB,
arc AP = arc BP
∠AOP = ∠BOP
∠AOM = ∠BOM
Considering triangles AOM and BOM,
OA = OB = radius of circle
OM = OM = common side
Also, ∠AOM = ∠BOM
By SAS criterion, the triangles AOM and BOM are similar.
Corresponding parts of congruent triangles or cpct is used to denote the relation between the sides and the angles of two congruent triangles.
By cpct,
∠AMO = ∠BMO --------- (1)
The linear pair angles ∠AMO + ∠BMO = 180°
From (1), ∠AMO + ∠AMO = 180°
2∠AMO = 180°
∠AMO = 90°
So, ∠AMO = ∠BMO = 90°
We know that the corresponding angles are equal.
From the figure,
∠BMO = ∠OPT = 90°
This implies AB || PT
Therefore, the tangent at midpoint of the arc is parallel to the chord joining the end points of the arc.
Q.10. In Fig. 9.19, the common tangent, AB and CD to two circles with centres O and O' intersect at E. Prove that the points O, E, O' are collinear.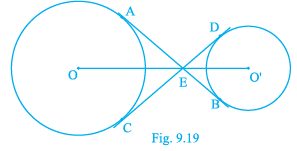
Given, the tangents AB and CD are common to two circles with centres O and O’
The common tangents AB and CD intersect at E.
We have to prove that the points O, E and O’ are collinear.Join OA and OC, O’D and O’B
Considering triangles AOE and EOC,
OE = OE = common side
OA = OC = radius of circle
We know that the radius of a circle is perpendicular to the tangent at the point of contact.
Tangents from external point E are EA and EC
So, AE = EC
By SAS criterion, the triangles AOE and EOC are similar.
Corresponding parts of congruent triangles or cpct is used to denote the relation between the sides and the angles of two congruent triangles.
By cpct,
∠AEO = ∠CEO ------------------ (1)
From the figure,
∠AEC = ∠AEO + ∠CEO
From (1), ∠AEC = ∠AEO + ∠AEO
∠AEC = 2∠AEO ------------------- (2)
From the figure,
CD is a straight line
The linear pair of angles ∠AED + ∠AEC = 180°
From (2), 2∠AEO + ∠AED = 180°
Dividing by 2,
∠AEO + (1/2)∠AED = 90°
∠AEO = 90° - (1/2)∠AED --------------- (3)
Considering triangles O’ED and O’EB,
O’B = O’D = radius of circle
O’E = O’E = common side
We know that the tangents drawn to a circle through an external point are equal.
So, EB = ED
By SSS criterion, the triangles O’ED and O’EB are similar.
By cpct, ∠O’ED = ∠O’EB ------------ (4)
From the figure,
∠DEB = ∠O’EB + ∠O’E
From (4), ∠DEB = ∠O’ED + ∠O’ED
∠DEB = 2∠O’ED ------------- (5)
From the figure,
AB is a straight line
The linear pair of angles ∠AED + ∠DEB = 180°
From (5), ∠AED + 2∠O’ED = 180°
Dividing by 2,
(1/2)∠AED + ∠O’ED = 90°
∠O’ED = 90° - (1/2)∠AED -------------- (6)
Adding ∠AEO + ∠AED + ∠O’ED ,
From (3) and (6),
= 90° - (1/2)∠AED + ∠AED + 90° - (1/2)∠AED
= 180° - ∠AED + ∠AED
= 180°
So, ∠AEO + ∠AED + ∠O’ED = 180°
The points O, E and O’ lie on the same line.
Therefore, the points E, O and O’ are collinear.
Q.11. In Fig. 9.20. O is the centre of a circle of radius 5 cm, T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.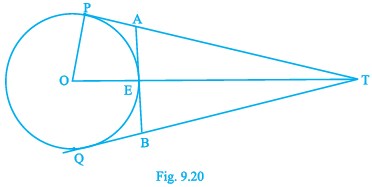
Given, O is the centre of a circle of radius 5 cm.
T is a point outside the circle such that OT = 13 cm.
OT intersects the circle at E.
We have to find the length of AB if AB is the tangent to the circle at EWe know that tangents to a circle through an external point are equal.
From point A, the tangents to the circle are AP and AE
So, AP = AE
Let AP = AE be x.
We know that the radius of a circle is perpendicular to the tangent at the point of contact.
So, OP ⟂ PT and OQ ⟂ QT
Also, ∠OPT = ∠OQT = 90°
Considering triangle OPT,
∠P = 90°
So, OPT is a right triangle with P at right angle.
By pythagoras theorem,
OT² = OP² + PT²
(13)² = (5)² + PT²
169 = 25 + PT²
PT² = 169 - 25
PT² = 144
Taking square root,
PT = 12 cm
Considering triangle AET,
∠E = 90°
So, AET is a right triangle with E at right angle.
By pythagoras theorem,
AT² = AE² + ET²
From the figure,
PT = PA + AT
12 = x + AT
AT = 12 - x
(12 - x)² = x² + ET²
ET² = (12 - x)² - x²
By using algebraic identity,
(a - b)² = a² - 2ab + b²
So, ET² = 144 - 24x + x² - x²
ET² = 144 - 24x
From the figure,
OT = OE + ET
13 = 5 + ET
ET = 13 - 5
ET = 8 cm
So, (8)² = 144 - 24x
64 = 144 - 24x
24x = 144 - 64
24x = 80
x = 80/24
x = 20/6
x = 10/3 cm
We know AB = 2(AE)
AB = 2(10/3)
AB = 20/3
AB = 6.6 cm
Therefore, the length of AB is 6.6 cm
Q.12. The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA =110º , find ∠CBA [see Fig. 9.21]. [Hint: Join C with centre O.]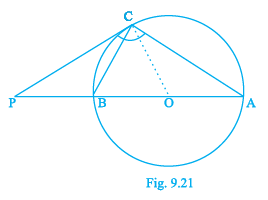
Given, O is the centre of a circle.
AB is the diameter of the circle
AB is extended to P and PC is a tangent to the circle at point C.
Given, ∠PCA = 110º
We have to find ∠CBAWe know that angle in a semicircle is always equal to 90°
So, ∠BCA = 90°
We know that the radius of a circle is perpendicular to the tangent at the point of contact.
i.e., OC ⟂ PC
So, ∠OCP = 90°
From the figure,
∠PCA = ∠BCA + ∠PCB
110° = 90° + ∠PCB
∠PCB = 110° - 90°
∠PCB = 20°
By alternate segment theorem,
We know that the angle between the tangent and the chord of a circle is equal to the angle made by the chord in the alternate segment.
∠PCB = ∠CAB
So, ∠CAB = 20°
Considering triangle ABC,
We know that the sum of all three interior angles of a triangle is equal to 180°
∠BCA + ∠CBA + ∠CAB = 180°
90° + ∠CBA + 20° = 180°
110° + ∠CBA = 180°
∠CBA = 180° - 110°
Therefore, ∠CBA = 70°
Q.13. If an isosceles triangle ABC, in which AB = AC = 6 cm, is inscribed in a circle of radius 9 cm, find the area of the triangle.
Given, ABC is an isosceles triangle
The measure of sides AB = AC = 6 cm
ABC is inscribed in a circle of radius 9 cm.
We have to find the area of the triangle.From the figure,
O is the centre of the circle
Join OB and OC.
Let M be the midpoint of BC.
So, OM ⟂ BC
In an isosceles triangle, the median from the vertex is perpendicular to the base.
Since, ABC is an isosceles triangle and M is the midpoint of BC.
AM ⟂ BC
Let AM = x
Let MB = CM = y
Considering triangle AMB,
AMB is a right triangle with M at right angle.
By pythagoras theorem,
AB² = AM² + BM²
(6)² = x² + y²
x² + y² = 36 ------------- (1)
Considering triangle OMB,
OMB is a right triangle with M at right angle.
OB² = OM² + BM²
OB = OC = 9 (radius of the circle)
From the figure,
AM + MO = AO
AO = radius of circle
x + OM = 9
OM = 9 - x
So, (9)² = (9 - x)² + y²
By algebraic identity,
(a - b)² = a² - 2ab + b²
Now, 81 = 81 - 18x + x² + y²
x² + y² = 18x ------------ (2)
Comparing (1) and (2),
36 = 18x
x = 36/18
x = 2 cm
So, AM = 2 cm
Put x = 2 in (1),
(2)² + y² = 36
4 + y² = 36
y² = 36 - 4
y² = 32
Taking square root,
y = 4√2 cm
Area of triangle = (1/2) × base × height
Area of triangle ABC = (1/2) × BC × AM
BC = BM + CM
= 4√2 + 4√2
BC = 8√2 cm
Area of triangle ABC = (1/2) × 8√2 × 2
= 8√2 square cm
Therefore, the area of the triangle is 8√2 square cm.
Q.14. A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm.
AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
Given, A is a point at a distance of 13 cm from the centre O of a circle of radius 5 cm.
AP and AQ are the tangents to the circle at P and Q.
A tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C.
We have to find the perimeter of the triangle ABC.From the figure,
Radius of the circle = OP = OQ = 5 cm
Given, OA = 13 cm
We know that the tangents drawn to a circle through an external point are equal.
Given, AP and AQ are the tangents to the circle from an external point A.
So, AP = AQ ------------------- (1)
We know that the radius of the circle is perpendicular to the tangent at the point of contact.
So, OP ⟂ PA and OQ ⟂ AQ
Also, ∠OPA = ∠OQA = 90°
Considering triangle OPA,
OPA is a right triangle with P at right angle.
By pythagoras theorem,
OA² = OP² + PA²
(13)² = (5)² + PA²
169 = 25 + PA²
PA² = 169 - 25
PA² = 144
Taking square root,
PA = 12 cm
Perimeter of a triangle is the sum of all three sides of the triangle.
Perimeter of triangle ABC = AB + BC + AC
From the figure,
BC = BR + CR
Perimeter of triangle ABC = AB + BR + CR + AC
We know that the tangents drawn to a circle through an external point are equal.
Tangents from external point B are BP and BR
So, BP = BR
Tangents from external point C are CQ and CR
So, CQ = CR
Perimeter of triangle ABC = AB + BR + CR + AC
= AB + BP + CQ + AC
We know AP = AB + BP
So, Perimeter of triangle ABC = AP + CQ + AC
From the figure,
AQ = AC + CQ
Now, Perimeter of triangle ABC = AP + AQ
From (1), AP + AP = 2 AP
Perimeter of triangle ABC = 2AP
= 2(12)
= 24 cm
Therefore, the perimeter of triangle ABC is 24 cm.
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Exemplar: Circles - Mathematics (Maths) Class 10
| 1. What is the definition of a circle? |  |
| 2. How is the radius of a circle related to its diameter? |  |
| 3. Can a circle have more than one center? |  |
| 4. How is the circumference of a circle calculated? |  |
| 5. What is the relationship between the radius and the area of a circle? |  |




















