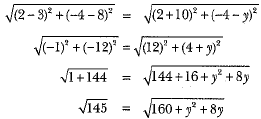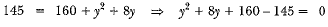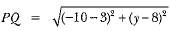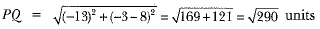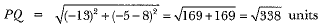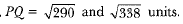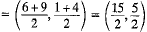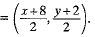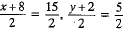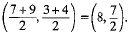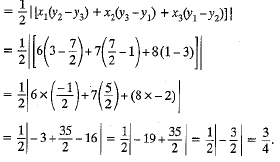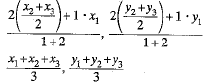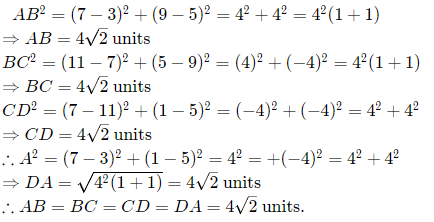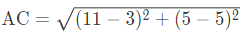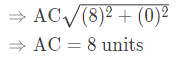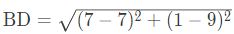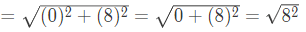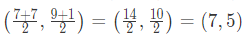NCERT Exemplar: Coordinate Geometry - 2 | Mathematics (Maths) Class 10 PDF Download
EXERCISE 7.3
Q.1. Name the type of triangle formed by the points A (–5, 6), B (–4, –2) and C (7, 5).
Given, the points are A(-5, 6) B(-4, -2) and C(7, 5)
We have to find the type of triangle ABC.
The distance between two points P (x1 , y1) and Q (x2 , y2) is
√[(x2 - x1)2 + (y2 - y1)2]
Distance between A(-5, 6) and B(-4, -2) = √[(-4 - (-5))2 + (-2 - 6)2]
= √[(1)² + (-8)²]
= √(1 + 64)
= √65
Distance between B(-4, -2) and C(7, 5) = √[(7 - (-4))² + (5 - (-2))²]
= √[(11)2 + (7)2]
√(121 + 49)
= √170
Distance between A(-5, 6) and C(7, 5) = √[(7 - (-5))2 + (5 - 6)2]
= √[(12)2 + (-1)2]
= √(144 + 1)
= √145
We know that a scalene triangle is a triangle in which all three sides have different lengths.
AB ≠ BC ≠ AC
The three sides of the triangle are in different lengths.
Therefore, the given points represent a scalene triangle.
Q.2. Find the points on the x–axis which are at a distance of 2√5 from the point (7, –4). How many such points are there?
Given, the points on the x-axis are at a distance of 2√5 from the point (7, -4).
We have to find the number of points that are at a distance of 2√5 from the point (7, -4).
The points on the x-axis mean the point represents the form (x, 0)
Let the given point be B = (7, -4)
Let the point on the x-axis be A(x, 0)
The distance between two points P (x1 , y1) and Q (x2 , y2) is
√[(x2 - x1)2 + (y2 - y1)2]
Distance between A(x, 0) and B(7, -4) = 2√5
√[(x2 - x1)2 + (y2 - y1)2] = 2√5
√[(7 - x)² + (-4 - 0)2] = 2√5
√[(7 - x)² + (-4)²] = 2√5
On squaring both sides,
(7 - x)2 + 16 = 20
By using algebraic identity,
(a - b)2 = a2 - 2ab + b2
So, (7 - x)2 = (7)2 - 2(7)(x) + (x)²
= 49 - 14x + x2
49 - 14x + x2 + 16= 20
x2 - 14x + 49 - 20 + 16 = 0
x2 - 14x + 45 = 0
x2 - 9x - 5x + 45 = 0
x(x - 9) - 5(x - 9) = 0(x - 5)(x - 9) = 0
Now, x - 5 = 0
x = 5
Also, x - 9 =0
x = 9
Therefore, the points (5, 0) and (9, 0) are at a distance of 2√5 from the point (7, -4).
Q.3. What type of a quadrilateral do the points A (2, –2), B (7, 3), C (11, –1) and D (6, –6) taken in that order, form?
Given, the points are A(2, -2) B(7, 3) C(11, -1) and D(6, -6)
We have to find the type of a quadrilateral formed by the given points.
The distance between two points P (x1 , y1) and Q (x2 , y2) is
√[(x2 - x1)2 + (y2 - y1)2]
Distance between A(2, -2) and B(7, 3) = √[(7 - 2)2 + (3 - (-2))2]
= √[(5)2 + (5)2]
= √(25 + 25)
= 5√2
Distance between B(7, 3) and C(11, -1) = √[(11 - 7)2 + (-1 - 3)2]
= √[(4)2 + (-4)2]
= √(16 + 16)
= 4√2
Distance between C(11, -1) and D(6, -6) = √[(6 - 11)2 + (-6 - (-1))2]
= √[(-5)2 + (-5)2]
= √(25 + 25)
= 5√2
Distance between A(2, -2) and D(6, -6) = √[(6 - 2)2 + (-6 - (-2))2]
= √[(4)2 + (-4)2]
= √(16 + 16)
= 4√2
Distance between A(2, -2) and C(11, -1) = √[(11 - 2)2 + (-1 - (-2))2]
= √[(9)2 + (1)2]
= √(81 + 1)
= √82
Distance between B(7, 3) and D(6, -6) = √[(6 - 7)2 + (-6 - 3)2]
= √[(-1)2 + (-9)2]
= √(81 + 1)
= √82
We observe that AB = CD and BC = AD.
Also, AC = BD
The opposite sides of the quadrilateral are equal.
The diagonals of the quadrilateral are equal.
Therefore, the given points represent a rectangle.
Q.4. Find the value of a, if the distance between the points A (–3, –14) and B (a, –5) is 9 units.
Given, the distance between the points A(-3, -14) and B(a, -5) is 9 units.
We have to find the value of a.
The distance between two points P (x1 , y1) and Q (x2 , y2) is
√[(x2 - x1)2 + (y2 - y1)2]
Now, distance between the points A (-3, -14) and B(a, -5) is
√[(a - (-3))2 + (-5 - (-14))2] = 9
√[(a + 3)2 + (-5 + 14)2] = 9
√[(a + 3)2 + (9)2] = 9
On squaring both sides,
(a + 3)2 + 81 = 81
(a + 3)2 = 81 - 81
(a + 3)2= 0
Taking square root,
a + 3 = 0
a = -3
Therefore, the value of a is -3.
Q.5. Find a point which is equidistant from the points A (–5, 4) and B (–1, 6)? How many such points are there?
Given, the points are A(-5, 4) and B(-1, 6)
We have to find a point which is equidistant from the given points.
Let the point P(x, y) be equidistant from the points A(-5, 4) and B(-1, 6)
So, PA = PB
The distance between two points P (x1 , y1) and Q (x2 , y2) is
√[(x2 - x1)2 + (y2 - y1)2]
Distance between P(x, y) and A(-5, 4) = √[(-5 - x)2 + (4 - y)2]
Distance between P(x, y) and B(-1, 6) = √[(-1 - x)2 + (6 - y)2]
Now, √[(-5 - x)2 + (4 - y)2] = √[(-1 - x)2 + (6 - y)2]
On squaring both sides,
(-5 - x)2 + (4 - y)2 = (-1 - x)2 + (6 - y)²
By using algebraic identity,
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
25 + 10x + x2 + y2 - 8y + 16 = x2 + 2x + 1 + y2 - 12y + 36
x2 + y2 + 10x - 8y + 41 = x2 + y2 + 2x - 12y + 37
Canceling out common terms,
10x - 8y + 41 = 2x - 12y + 37
By grouping,
10x - 2x - 8y + 12y + 41 - 37 = 0
8x + 4y + 4 = 0
Dividing by 4,
2x + y + 1 = 0 ---------------- (1)
The coordinates of the mid-point of the line segment joining the points P (x₁ , y₁) and Q (x₂ , y₂) are [(x1 + x2)/2, (y2 + y2)/2]
Midpoint of A(-5, 4) and B(-1, 6) = [(-5 + (-1))/2, (6 + 4)/2]
= [-6/2, 10/2]
= (-3, 5)
Verification:
Substitute (-3, 5) in (1)
So, 2(-3) + 5 + 1 = 0
-6 + 6 = 0
It is clear that the midpoint of AB satisfies the equation (1).
The solution of the equation 2x + y + 1 = 0 are all equidistant from the points A and B.
Therefore, there are an infinite number of points that are equidistant from the points A and B.
Q.6. Find the coordinates of the point Q on the x–axis which lies on the perpendicular bisector of the line segment joining the points A (–5, –2) and B(4, –2). Name the type of triangle formed by the points Q, A and B.
Given, the point Q on the x-axis lies on the perpendicular bisector of the line segment joining the points A(-5, -2) and B(4, -2).
We have to find the type of triangle formed by the points Q, A and B.
The point Q lies on the x-axis means Q = (x, 0)
We know that any point lying on the perpendicular bisector of the line segment joining two points is equidistant from the two points.
The perpendicular bisector joining the two points are A(-5, -2) and B(4, -2)
To check if the point Q lies on the perpendicular bisector, then distance between QA must be equal to distance between QB i.e., QA = QB
The distance between two points P (x1 , y1) and Q (x2 , y2) is
√[(x2 - x1)2 + (y2 - y1)2]Distance between Q(x, 0) and A(-5, -2) = √[(-5 - x)2 + (-2 - 0)2]
= √[(-5 - x)2 + (-2)2]
= √[(-5 - x)2 + 4]
Distance between Q(x, 0) and B(4, -2) = √[(4 - x)2 + (-2 - 0)²]
= √[(4 - x)2 + (-2)2]
= √[(4 - x)2 + 4]
Now, √[(-5 - x)2 + 4] = √[(4 - x)2 + 4]
On squaring both sides,
(-5 - x)2 + 4 = (4 - x)2 + 4
Canceling out common terms,
(-5 - x)2 = (4 - x)2
By using algebraic identity,
(a + b)2 = a2 + 2ab + b2(a - b)2 = a2 - 2ab + b2
25 + 10x + x2 = 16 - 8x + x2
By grouping,
x2 - x2 + 10x + 8x + 25 - 16 = 0
18x + 9 = 0
18x = -9
x = -9/18
x = -1/2
Therefore, the point Q is (-1/2, 0)
Distance between A(-5, -2) and B(4, -2) = √[(4 - (-5))2 + (-2 - (-2))2]
= √[(4+5)2 + (-2 + 2)2]
= √81
= 9
Distance between Q(-1/2, 0) and B(4, -2) = √[(4 + (1/2))2 + 4]
= √[(4.5)2 + 4]
= √24.25
Distance between Q(-1/2, 0) and A(-5, -2) = √[(-5 + 0.4)² + 4]
= √[(4.5)2 + 4]
= √24.25
It is clear that QA = QB
Two sides of a triangle are equal.
Therefore, the points Q, A and B form an isosceles triangle.
Q.7. Find the value of m if the points (5, 1), (–2, –3) and (8, 2m ) are collinear
Given, the points (5, 1) (-2, -3) and (8, 2m) are collinear.
We have to find the value of m.
The area of a triangle with vertices A (x1 , y1) , B (x2 , y2) and C (x3 , y3) is
1/2[x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
To check for the points to be collinear, the area of the triangle must be zero.
Here, (x1 , y1) = (5, 1), (x2 , y2) = (-2, -3) and (x3 , y3) = (8, 2m)
Area of triangle = 1/2[5(-3 - 2m) + -2(2m - 1) + 8(1 - (-3))] = 0
-15 - 10m - 4m + 2 + 8(4) = 0
-13 - 14m + 32 = 0
-14m + 19 = 0
14m = 19
m = 19/14
Therefore, the value of m is 19/14.
Q.8. If the point A (2, -4) is equidistant from P (3, 8) and Q (-10, 3)), find the values of y. Also find distance PQ.
Given points are A (2, -4), P(3, 8) and Q(—10, y)
According to the question,
PA = QA
On squaring both sides, we get
y2 + 8y + 15 = 0
y2 + 5y + 3y + 15 = 0
⇒ y(y + 5) + 3(y + 5) = 0
⇒ (y+ 5) (y + 3) = 0
⇒ y + 5 = 0
⇒ y = -5
and y + 3 = 0
⇒ y = -3
∴ y = -3, -5
Now,
For y = -3
and for y = -5
Hence, values of y are - 3 and -5,
Q.9. Find the area of the triangle whose vertices are (–8, 4), (–6, 6) and (–3, 9).
Given, the vertices of the triangle are (-8, 4) (-6, 6) and (-3, 9)
We have to find the area of the triangle.
The area of a triangle with vertices A (x1 , y1) , B (x2 , y2) and C (x3 , y3) is
1/2[x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
Here, (x1 , y1) = (-8, 4) (x2 , y2) = (-6, 6) and (x3 , y3) = (-3, 9)
Area of the triangle = 1/2[-8(6 - 9) + -6(9 - 4) + -3(4 - 6)]
= 1/2[-8(-3) - 6(5) - 3(-2)]
= 1/2[24 - 30 + 6]
= 1/2[-6 + 6]
= 0Therefore, the area of the triangle = 0 square units.
Q.10. In what ratio does the x–axis divide the line segment joining the points (– 4, – 6)
and (–1, 7)? Find the coordinates of the point of division.
Given, the line segment joining the points (-4, -6) and (-1, 7)
We have to find the ratio of division of the line segment and the coordinates of the point of division.
By section formula,
The coordinates of the point P(x, y) which divides the line segment joining the points A (x1 , y1) and B (x2 , y2) internally in the ratio k : 1 are [(kx2 + x1)/(k + 1) , (ky2+ y1)/(k + 1)]
Here, (x1 , y1) = (-4, -6) and (x2 , y2) = (-1, 7)
So, [(k(-1) + (-4))/(k + 1) , (k(7) + (-6))/(k + 1)] = k:1
[(-k - 4)/(k + 1), (7k - 6)/(k + 1)] = k:1
The point lies on the x-axis. i.e., y = 0
So, 7k - 6/k + 1 = 0
7k - 6 = 0
7k = 6
k = 6/7
Therefore, the ratio of division is 6:7.
To find the coordinates of the point of division, x coordinates is (m1x2 + m2x1)/(m1 + m2)
Here, m1:m2 = 6:7, (x1 , y1) = (-4, -6) and (x2 , y2) = (-1, 7)
= [6(-1) + 7(-4)]/(6 + 7)
= -6 - 28/13
= -34/13
Therefore, the coordinate of the point of division is (-34/13, 0).
Q.11. Find the ratio in which the point 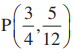 divides the line segment joining the
divides the line segment joining the
points 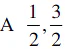 and B (2, –5).
and B (2, –5).
Given, point P(3/4, 5/12) divides the line segment joining the points A(1/2, 3/2) and B(2, -5).
We have to find the ratio in which the point P divides the line segment AB.
By section formula,
The coordinates of the point P(x, y) which divides the line segment joining the points A (x1 , y1) and B (x2 , y2) internally in the ratio k : 1 are [(kx2 + x1)/(k + 1), (ky2 + y1)/(k + 1)]
Here, (x1, y1) = (1/2, 3/2) and (x2, y2) = (2, -5)
[(k(2) + (1/2))/(k + 1) , (k(-5) + (3/2))/(k + 1)] = (3/4, 5/12)
[(2k + (1/2))/(k + 1), (-5k + (3/2))/(k + 1)] = (3/4, 5/12)
Now, (2k + (1/2))/(k + 1) = 3/4
2k + (1/2) = 3/4(k + 1)
(4k + 1)/2 = (3k + 3)/4
4k + 1 = (3k + 3)/2
2(4k + 1) = 3k + 3
8k + 2 = 3k + 3
8k - 3k = 3 - 2
5k = 1
k = 1/5
Also, (-5k + (3/2))/(k + 1) = 5/12
-5k + (3/2) = 5/12(k + 1)
(-10k + 3)/2 = (5k + 5)/12
(-10k + 3) = (5k + 5)/6
6(-10k + 3) = 5k + 5
-60k + 18 = 5k + 5
18 - 5 = 5k + 60k
65k = 13
k = 13/65
k = 1/5
Therefore, the required ratio is 1:5
Q.12. If P (9a – 2, –b) divides line segment joining A (3a + 1, –3) and B (8a, 5) in the
ratio 3 : 1, find the values of a and b.
Given, point P(9a - 2, -b) divides the line segments joining A(3a + 1, -3) and B(8a, 5) in the ratio 3:1
We have to find the values of a and b.
The coordinates of the point P which divides the line segment joining the points A (x₁ , y₁) and B (x2 , y2) internally in the ratio m₁ : m₂ are
[(m1x2 + m2x1)/(m1 + m2) , (m1y2 + m2y1)/(m1 + m2)]
Here, m1:m2 = 3:1, (x1 , y1) = (3a + 1, -3) and (x2 , y2) = (8a, 5)
So, [(3(8a) + 1(3a + 1))/(3 + 1), (3(5) + 1(-3))/(3 + 1)] = (9a - 2, -b)
[(24a + 3a + 1)/4, (15 - 3)/4] = (9a - 2, -b)
[(27a + 1)/4, 12/4] = (9a - 2, -b)
Now, (27a + 1)/4 = 9a - 2
27a + 1 = 4(9a - 2)
27a + 1 = 36a - 8
36a - 27a = 1 + 8
9a = 9
a = 9/9
a = 1
Also, -b = 12/4
-b = 3
b = -3Therefore, the values of a and b are 1 and -3.
Q.13. If (a, b) is the mid-point of the line segment joining the points A (10, –6) and
B (k, 4) and a – 2b = 18, find the value of k and the distance AB.
Given, (a, b) is the midpoint of the line segment joining the points A(10, -6) and B(k, 4).
Also, a - 2b = 18 -------------- (1)
We have to find the value of k and the distance AB
The coordinates of the mid-point of the line segment joining the points P (x1 , y1) and Q (x2 , y2) are [(x1 + x2)/2, (y1 + y2)/2]
Here, (x1 , y1) = (10, -6) and (x2 , y2) = (k, 4)
Midpoint of AB, [(10 + k)/2, (-6 + 4)/2] = (a, b)
[(10 + k)/2, -2/2] = (a, b)
Now, (10 + k)/2 = a
10 + k = 2a
k = 2a - 10 ---------------- (2)
Also, b = -2/2
b = -1
Put b = -1 in (1)
a - 2(-1) = 18
a + 2 = 18
a = 18 - 2
a = 16
Put a = 16 in (2)
k = 2(16) - 10
k = 32 - 10
k = 22
Therefore, the value of k is 22.
The distance between two points P (x1 , y1) and Q (x2 , y2) is √[(x2 - x1)² + (y2 - y1)²]
Distance between A(10, -6) and B(22, 4) = √[(22 - 10)2 + (4 - (-6))2]
= √[(12)2 + (10)2]
= √(144 + 100)
= √244
= 2√61
Therefore, the distance between A and B is 2√61 units.
Q.14. The centre of a circle is (2a, a – 7). Find the values of a if the circle passes
through the point (11, –9) and has diameter 10√2 units.
Given, the center of a circle is (2a, a - 7)
The circle passes through the point (11, -9)
The diameter of the circle is 10√2 units.
We have to find the value of a.
Distance between the center and the point = radius of the circle
Radius of the circle = 10√2/2 = 5√2 units
The distance between two points P (x1 , y1) and Q (x2 , y2) is √[(x2 - x1)2 + (y2 - y1)2]
Distance between (2a, a -7) and (11, -9) = 5√2
√[(11 - 2a)2 + (-9 - (a - 7))2] = 5√2
√[(11 - 2a)2 + (-9 - a + 7)2] = 5√2
√[(11 - 2a)2+ (-a - 2)2] = 5√2
On squaring both sides,
(11- 2a)2 + (a + 2)2 = 50
By using algebraic identity,
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
(11 - 2a)2 = 121 - 44a + 4a2
(a + 2)2 = a2 + 4a + 4
Now, 121 - 44a + 4a2 + a2 + 4a + 4 = 50
By grouping,
4a² + a² - 44a + 4a + 121 + 4 = 50
5a² - 40a + 125 - 50 = 0
5a2 - 40a + 75 = 0
Dividing by 5,
a2 - 8a + 15 = 0
a2 - 5a - 3a + 15 = 0
a(a - 5) - 3(a - 5) = 0
(a - 3)(a - 5) = 0
Now, a - 3 = 0
a = 3
Also, a - 5 = 0
a = 5
Therefore, the values of a are 3 and 5.
Q.15. The line segment joining the points A (3, 2) and B (5,1) is divided at the point P in
the ratio 1:2 and it lies on the line 3x – 18y + k = 0. Find the value of k.
Given, the line segment joining the points A(3, 2) and B(5, 1) is divided at the point P in the ratio 1:2
The point P lies on the line 3x - 18y + k = 0
We have to find the value of k.
The coordinates of the point P which divides the line segment joining the points A (x₁ , y₁) and B (x2 , y2) internally in the ratio m₁ : m₂ are
[(m₁x2+m2x1)/(m₁+m2) , (m1y2+m2y1)/(m1+m2)]
Here, m1:m2 = 1:2, (x1 , y1) = (3, 2) and (x2 , y2) = (5, 1)
Let the point P be (x, y)
[(1(5) + 2(3))/(1 + 2), (1(1) + 2(2))/(1 + 2)] = (x, y)
[(5 + 6)/3, (1 + 4)/3] = (x, y)
[11/3, 5/3] = (x, y)
The point P is (11/3, 5/3)
The point P lies on the line 3x - 18y + k = 0
So, 3(11/3) - 18(5/3) + k = 0
11 - 6(5) + k = 0
11 - 30 + k = 0
-19 + k = 0
k = 19
Therefore, the value of k is 19.
Q.16. If 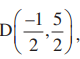 E (7, 3) and
E (7, 3) and 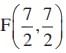 are the midpoints of sides of ∆ ABC, find the area of the ∆ ABC.
are the midpoints of sides of ∆ ABC, find the area of the ∆ ABC.
Given, the midpoints of sides of ∆ ABC are D(-1/2, 5/2) E(7, 3) and F(7/2, 7/2)
We have to find the area of the ∆ ABC.
Let A = (x1, y1) B = (x2, y2) and C(x3, y3)The coordinates of the mid-point of the line segment joining the points P (x1 , y1) and Q (x2 , y2) are [(x1 + x2)/2, (y1 + y2)/2]
Midpoint of AB = D
[(x1 + x2)/2, (y1 + y2)/2] = (-1/2, 5/2)
Now, (x1 + x2)/2 = -1/2
x1 + x2 = -2/2
x1 + x2 = -1 ----------- (1)
Also, (y1 + y2)/2 = 5/2
y1 + y2 = 5 ------------ (2)
Midpoint of BC = E
[(x2 + x3)/2, (y2 + y3)/2] = (7, 3)
Now, (x2 + x3)/2 = 7
x2 + x3 = 14 ------------------ (3)
Also, (y2 + y3)/2 = 3
y2 + y3 = 6 -------------------- (4)
Midpoint of AC = F
[(x1 + x3)/2, (y1 + y3)/2] = (7/2, 7/2)
Now, (x1 + x3)/2 = 7/2
x1 + x, = 7 ---------------- (5)
Also, (y1 + y3)/2 = 7/2
y1+y3 = 7 ---------------- (6)
Adding (1), (3) and (5) we get,
2(x1 + x2 + x3) = -1 + 14 + 7
2(x1 + x2 + x3) = 20
x1 + x2 + x3 = 10 --------------- (7)
Substitute (1) in (7),
-1 + x3 = 10
x3 = 11
Substitute (2) in (7),
x1 + 14 = 10
x1 = 10 - 14
x1 = -4
Substitute (3) in (7),
x2 + 7 = 10
x2 = 10 - 7
x2 = 3
Adding (2), (4) and (6) we get,
2(y1 + y2 + y3) = 5 + 6 + 7
2(y1 + y2 + y3) = 18
y1 + y2 + y3 = 9 ------------------ (8)
Substitute (2) in (8),
5 + y3 = 9
y3 = 9 - 5
y3 = 4
Substitute (4) in (8),
y1 + 6 = 9
y1 = 9 - 6
y1 = 3
Substitute (6) in (8),
y2 + 7 = 9
y2 = 9 - 7
y2 = 2
Therefore, the vertices of ∆ ABC are A(-4, 3) B(3, 2) and C(11, 4).
The area of a triangle with vertices A (x1 , y1) , B (x2 , y2) and C (x3 , y3) is
1/2[x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
Here, (x1 , y1) = (-4, 3) (x2 , y2) = (3, 2) and (x3 , y3) = (11, 4)
Area of triangle ABC = 1/2[-4(2 - 4) + 3(4 - 3) + 11(3 - 2)]
= 1/2[-4(-2) + 3(1) + 11(1)]
= 1/2[8 + 3 + 11]
= 1/2[11 + 11]
= 1/2[22]
= 11 square units.
Therefore, the area of triangle ABC is 11 square units.
Q.17. The points A (2, 9), B (a, 5) and C (5, 5) are the vertices of a triangle ABC right
angled at B. Find the values of a and hence the area of ∆ABC.
Given, the vertices of a triangle ABC right angled at B are A(2, 9) B(a, 5) and C(5, 5).
We have to find the value of a and the area of the triangle ABC.
Since the triangle ABC is a right triangle with B at right angle.
By pythagoras theorem,
AC2 = AB2 + BC2
The distance between two points P (x1 , y1) and Q (x2 , y2) is
√[(x2 - x1)2 + (y2 - y1)2]
Distance between A(2, 9) and C(5, 5) = √[(5 - 2)2 + (5 - 9)2]
= √[(3)2 + (-4)²]
= √(9 + 16)
= √25
= 5
Distance between A(2, 9) and B(a, 5) = √[(a - 2)2 + (5 - 9)2]
= √[(a - 2)2 + (-4)2]
= √[(a - 2)2 + 16]
Distance between B(a, 5) and C(5, 5) = √[(5 - a)2 + (5 - 5)2]
= √[(5 - a)2 + 0]
= √(5 - a)2
Now, (5)2 = (√[(a - 2)2 + 16])2 + (√(5 - a)2)2
25 = (a - 2)2 + 16 + (5 - a)2
By using algebraic identity,
(a - b)2 = a2 - 2ab + b2
Now, 25 = a2 - 4a + 4 + 16 + 25 - 10a + a2
25 = 2a2 -14a + 45
2a2 - 14a + 45 - 25 = 0
2a2 - 14a + 20 = 0
Dividing by 2,
a2 - 7a + 10 = 0
On factoring,
a2 - 5a - 2a + 10 = 0
a(a - 5) - 2(a - 5) = 0
(a - 2)(a - 5) = 0
Now, a - 2 = 0
a = 2
Also, a - 5 = 0
a = 5
The values of a are 2 and 5.
When a = 5, distance BC = √(5 - 5)2 = 0
So, a = 5 is not possible.
Therefore, the value of a is 2.
The area of a triangle with vertices A (x1, y1) , B (x2, y2) and C (x3, y3) is
1/2[x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
Here, (x1 , y1) = (2, 9) (x2 , y2) = (2, 5) and (x3 , y3) = (5, 5)
Area of triangle ABC = 1/2[2(5 - 5) + 2(5 - 9) + 5(9 - 5)]
= 1/2[0 + 2(-4) + 5(4)]
= 1/2[-8+20]
= 1/2[12]
= 6 square units.
Therefore, the area of the triangle ABC is 6 square units.
Q.18. Find the coordinates of the point R on the line segment joining the points
P (–1, 3) and Q (2, 5) such that PR = 3/5PQ.
Given, the point R lies on the line segment joining the points P(-1, 3) and Q(2, 5).
We have to find the coordinates of the point R such that PR = 3/5 PQ.
PR/PQ = 3/5
On rearranging,
PQ/PR = 5/3
We know that PQ = PR + QR
So, (PR + QR) / PR = 5/3
PR/PR + QR/PR = 5/3
1 + QR/PR = 5/3
QR/PR = 5/3 - 1
QR/PR = 5-3/3
QR/PR = 2/3
Again rearranging,
PR/QR = 3/2
PR : QR = 3 : 2
Therefore, the point R divides the line segment PQ in the ratio 3:2
The coordinates of the point P which divides the line segment joining the points A (x1 , y1) and B (x2 , y2) internally in the ratio m1 : m2 are
[(m1x2 + m2x1)/m1 + m2 , (m1y2 + m2y1)/m1 + m2]
Here, m1 : m2 = 3 : 2, (x1, y1) = (-1, 3) and (x2 , y2) = (2, 5)
Let the coordinate of R = (x, y)
(x, y) = [(3(2) + 2(-1))/3 + 2, (3(5) + 2(3))/3 + 2]
(x, y) = [(6 - 2)/5, (15 + 6)/5]
(x, y) = [4/5, 21/5]
Therefore, the coordinates of point R are (4/5, 21/5).
Q.19. Find the values of k if the points A (k + 1, 2k), B(3k, 2k + 3) and C(5k - 1, 5k) are collinear.
Given, the points A(k + 1, 2k) B(3k, 2k + 3) and C(5k - 1, 5k) are collinear.
We have to find the values of k.
To check for the points to be collinear, the area of the triangle must be zero.
The area of a triangle with vertices A (x1 , y1) , B (x2 , y2) and C (x3 , y3) is
1/2[x1(y2 - y3) + x2(y3 - y1) + x₃(y1 - y₂)]
Here, (x1 , y1) = (k + 1, 2k), (x2 , y2) = (3k, 2k + 3) and (x3 , y3) = (5k - 1, 5k)
Area of the triangle = 1/2[(k + 1)(2k + 3 - 5k) + 3k(5k - 2k) + (5k - 1)(2k - (2k + 3))] = 0
1/2[(k + 1)(3 - 3k) + 3k(3k) + (5k - 1)(-3)] = 0
By multiplicative and distributive property,
3k - 3k² + 3 - 3k + 9k² - 15k + 3 = 0
By grouping,
9k² - 3k² - 15k - 3k + 3k + 3 + 3 = 0
6k² - 15k + 6 = 0
Dividing by 3,
2k² - 5k + 2 = 0
On factoring,
2k² - 4k - k + 2 = 0
2k(k - 2) - 1(k - 2) = 0
(2k - 1)(k - 2) = 0
Now, 2k - 1 = 0
2k = 1
k = 1/2
Also, k - 2 = 0
k = 2
Therefore, the values of k are 1/2 and 2.
Q.20. Find the ratio in which the line 2x + 3y – 5 = 0 divides the line segment joining
the points (8, –9) and (2, 1). Also find the coordinates of the point of division.
Given, the line 2x + 3y - 5 = 0 divides the line segment joining the points (8, -9) and (2, 1)
We have to find the ratio in which the given line divides the line segment and the coordinates of the point of division.
By section formula,
The coordinates of the point P(x, y) which divides the line segment joining the points A (x1 , y1) and B (x1 , y1) internally in the ratio k : 1 are [(kx2 + x1)/k +1, (ky2 + y1)/k + 1]
Here, (x1 , y,) = (8, -9) and (x2 , y2) = (2, 1)
Let the coordinates of the point be (x, y)
[(k(2) + 8)/k + 1, (k(1) + (-9))/k + 1] = (x, y)
[(2k + 8)/k + 1, (k - 9)/k + 1] = (x, y) ----------------------- (1)
The point lies on the line 2x + 3y - 5 = 0.
Now, 2((2k + 8)/k + 1) + 3((k - 9)/k + 1) = 5
2(2k + 8) + 3(k - 9) = 5(k + 1)
4k + 16 + 3k - 27 = 5k + 5
By grouping,
4k + 3k - 5k = 5 + 27 - 16
7k - 5k = 5 + 11
2k = 16
k = 16/2
k = 8
Therefore, the point divides the line segment in the ratio 8 : 1.
To find the coordinates of the point of division,
Put k = 8 in (1)
(x, y) = [(2(8) + 8)/8 + 1, (8 - 9)/8 + 1]
(x, y) = [(16 + 8)/9, -1/9]
(x, y) = [24/9, -1/9]
(x, y) = [8/3, -1/9]
Therefore, the coordinates of the point of division are 8/3 and -1/9.
EXERCISE 7.4
Q.1. If (– 4, 3) and (4, 3) are two vertices of an equilateral triangle, find the coordinates
of the third vertex, given that the origin lies in the interior of the triangle.
Given, (-4, 3) and (4, 3) are the two vertices of an equilateral triangle.
Also, the origin lies in the interior of the triangle.
We have to find the coordinates of the third vertex.
Let an equilateral triangle be ABC.
The vertices of the triangle be A(-4, 3) B(4, 3) and the third vertex is (x, y).
An equilateral triangle is a triangle in which all three sides have the same length.
An equilateral triangle is also equiangular as all three internal angles are congruent to each other and are each 60°.
So, AB = BC = AC
Considering AB = BC
The distance between two points P (x1 , y1) and Q (x2 , y2) is
√[(x2 - x1)² + (y2 - y1)²]
Distance between A(-4, 3) and B(4, 3) = √[(4 - (-4))² + (3 - 3)²]
= √[(8)² + 0]
= √64
= 8
Distance between B(4, 3) and C(x, y) = √[(x - 4)² + (y - 3)²]
8 = √[(x - 4)² + (y - 3)²]
On squaring both sides,
64 = (x - 4)² + (y - 3)²
By using algebraic identity,
(a - b)² = a² - 2ab + b²
So, (x - 4)² = x² - 8x + 16
(y - 3)² = y² - 6y + 9
Now, 64 = x² - 8x + 16 + y² - 6y + 9
x² + y² - 8x - 6y = 64 - 25
x² + y² - 8x - 6y = 39 ------------------ (1)
Considering AB = AC,
Distance between A(-4, 3) and C(x, y) = √[(x - (-4))² + (y - 3)²]
= √[(x + 4)² + (y - 3)²]
Now, 8 = √[(x + 4)² + (y - 3)²]
On squaring both sides,
64 = (x + 4)² + (y - 3)²
By using algebraic identity,
(a + b)² = a² + 2ab + b²
So, (x + 4)² = x² + 8x + 16
64 = x² + 8x + 16 + y² - 6y + 9
x² + y² + 8x - 6y = 64 - 25
x² + y² + 8x - 6y = 39 ---------------- (2)
Subtracting (1) and (2),
x² + y² + 8x - 6y - (x² + y² - 8x - 6y) = 39 - 39
On simplification,
x² - x² + y² - y² + 8x - 6y + 8x + 6y = 0
8x + 8x = 0
16x = 0
x = 0
Put x = 0 in (1)
(0)² + y² - 8(0) - 6y = 39
y² - 6y - 39 = 0
Using the quadratic formula,
y = -b∙±√(b² - 4ac)/2a
Here, a = 1, b = -6 and c = -39
So, y = 6 ± √((-6)² - 4(1)(-39))/2(1)
= 6 ± √(36 + 156)/2
= (6 ± √192)/2
y = 3 ± 4√3
Now, y = 3 - 4√3
y = 3 + 4√3
Since the origin lies in the interior of the triangle, the x coordinate of the third vertex is zero.
y = 3 + 4√3 lies outside the triangle. So, it is not possible.
y = 3 - 4√3 lies inside the triangle.
Therefore, the coordinates of the third vertex = (0, 3 - 4√3)
Q.2. A (6, 1), B (8, 2) and C (9, 4) are three vertices of a parallelogram ABCD. If E is the mid
point of DC, find the area of ΔADE.
Let (x, y) be coordinates of D.
Since we know that diagonals of a parallogram bisect each other.
So, mid-point of AC
Mid-point of BD
Mid-point of AC and BD are
By comparison
x = 7, y = 3
Coordinates of D are (7, 3).
and coordinates of E are
Area of ΔADE
Q.3. The points A (x1, y1), B (x2, y2) and C (x3, y3) are the vertices of ΔABC.
(i) The-median from A meets BC at D. Find the coordinates of the point D.
(ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1.
(iii) Find the coordinates of points Q and R on medians BE and CF, respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
(iv) What are the coordinates of the centroid of the triangle ABC?
(i) D is mid-point of BC.
(ii) If P is point on AD, then by section formula
(iii) Given, the vertices of ∆ ABC are A (x1, y1), B (x2, y2) and C (x₃, y₃).The points Q and R are the points on medians BE and CF such that BQ:QE = 2:1 and
CR:RF = 2:1.
We have to find the coordinates of the points Q and R.
Let the coordinates of Q be (a, b) and R be (p, q).
The coordinates of the mid-point of the line segment joining the points P (x₁ , y₁) and Q (x₂ , y₂) are [(x1 + x2)/2, (y1 + y2)/2]
E is the midpoint of A(x1, y1) and C(x3, y3)
E = [(x1 + x3)/2, (y1 + y3)/2]
F is the midpoint of A(x1, y1) and B(x2 , y2)
F = [(x1 + x2)/2, (y1 + y2)/2]
By section formula,
The coordinates of the point P which divides the line segment joining the points A (x1 , y1) and B (x2 , y2) internally in the ratio m1 : m2 are
[(m1x2 + m2x1)/m1 + m2 , (m1y2 + m2y1)/m1 + m2]
The point Q divides the line B(x2 , y2) and E((x1 + x3)/2, (y1 + y3)/2) in the ratio 2:1
Coordinates of Q, (a, b) = [2(x1 + x3)/2 + 1(x2)/2 + 1, 2(y1 + y3)/2 + 1(y₂)/2 + 1]
(a, b) = [(x1 + x2 + x3)/3, (y1 + y2 +y3)/3]
The point R divides the line C(x3, y3) and F((x1 + x2)/2, (y1 + y2)/2) in the ratio 2:1
Coordinates of R, (p, q) = [2(x₁ + x3)/2 + 1(x2)/2 + 1, 2(y1 + y3)/2 + 1(y2)/2 + 1]
(p, q) = [(x1 + x2 + x3)/3, (y1 + y2 + y3)/3]
Therefore, the coordinates of Q and R ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3) and ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3).
(iv) Given, the vertices of ∆ ABC are A (x1, y1), B (x1, y1) and C (x₃, y₃).We have to find the centroid of the triangle ABC.
The centroid of a triangle is the point of intersection of the three medians of a triangle.
The formula for the centroid of the triangle is given by
C = (a + b + c)/3, (d + e + f)/3
Where, a, b, c are the x-coordinates of the vertices of the triangle
d, e, f are the y-coordinates of the vertices of the triangle.
The centroid of the triangle A(x1, y1), B (x2, y1) and C (x3, y3) is given as
C = [(x1 + x2 + x3)/3, (y1 + y2 + y3)/3]
Therefore, the centroid of the triangle ABC is (x1 + x2 + x3)/3, (y1 + y2 + y3)/3.
Q.4. If the points A (1, –2), B (2, 3) C (a, 2) and D (– 4, –3) form a parallelogram,
find the value of a and height of the parallelogram taking AB as base.
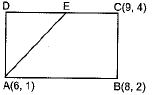
Q.5. Students of a school are standing in rows and columns in their playground for a
drill practice. A, B, C and D are the positions of four students as shown in
figure. Is it possible to place Jaspal in the drill in such a way that he is
equidistant from each of the four students A, B, C and D? If so, what should be
his position?

Coordinates of A, B, C and D from graph are A(3, 5), B(7, 9), C(11, 5), and D(7, 1).
To find the shape of ABCD,
So, ABCD will be either square or rhombus.
Now, Diagonal
and diagonal⇒BD=8 units
∴ Diagonal AC = Diagonal BD
So, the given quadrilateral ABCD is square. The point which is equidistant from point A, B, C, D of a square ABCD will be at the intersecting point of diagonals and diagonals bisect each other.
Hence, the required point O equidistant from A, B, C, D is mid point of any diagonal =
Hence, the required point is (7, 5).
Q.6. Ayush starts walking from his house to office. Instead of going to the office
directly, he goes to a bank first, from there to his daughter’s school and then
reaches the office. What is the extra distance travelled by Ayush in reaching his
office? (Assume that all distances covered are in straight lines).
If the house is situated at (2, 4), bank at (5, 8), school at (13, 14) and office at
(13, 26) and coordinates are in km.
Lets apply the distance formula to calculate the individual distances as below:
The position of Ayush’s house is (2, 4) and the position of the bank is (5, 8).
So, the distance between the house and the bank,
d1 = √[(5 – 2)2 + (8 – 4)2] = √[(3)2 + (4)2] = √[9 + 16] = √25 = 5 km
The position of the bank is (5, 8) and the position of the school is (13, 14).
So, the distance between the bank and the school
d2 = √[(13 – 5)2 + (14 – 8)2] = √[(8)2 + (6)2] = √[64 + 36] = √100 = 10 km
The position of the school is (13, 14) and the position of the office is (13, 26).
So, the distance between the school and the office,
d3 = √[(13 – 13)2 + (26 – 14)2] = √[(0)2 + (12)2] = √144 = 12 km
Let d be the total distance covered by Ayush
d = d1 + d2 + d3 = 5 + 10 + 12 = 27 km
Let the D be the shortest distance from Ayush’s house to the office,
D = √[(13 – 2)2 + (26 – 4)2] = √[(11)2 + (22)2] = √[121+ 484] = √605 = 24.6 km
Thus, the extra distance covered by Ayush = d – D = 27 – 24.6 = 2.4 km
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Exemplar: Coordinate Geometry - 2 - Mathematics (Maths) Class 10
| 1. What is coordinate geometry? |  |
| 2. How is coordinate geometry useful in real life? |  |
| 3. What are the basic concepts of coordinate geometry? |  |
| 4. How do you find the distance between two points in coordinate geometry? |  |
| 5. How can coordinate geometry help in solving equations of lines? |  |