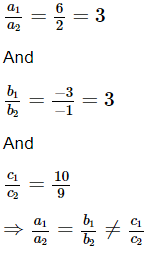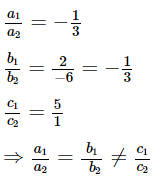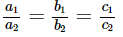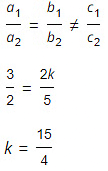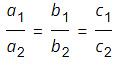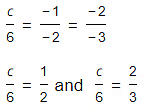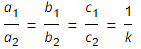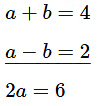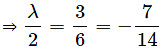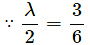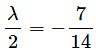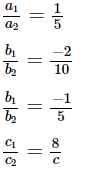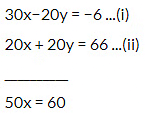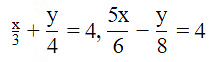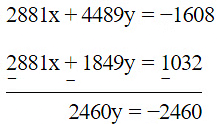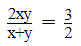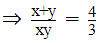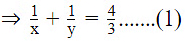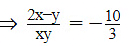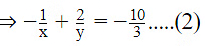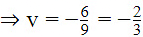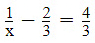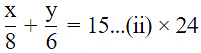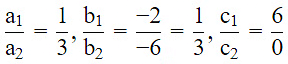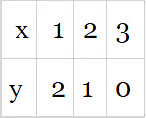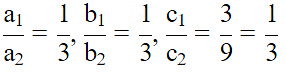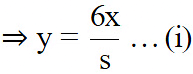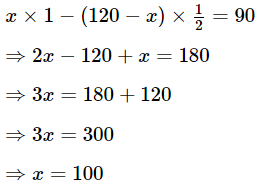NCERT Exemplar: Pair of Linear Equations in Two Variables- 1 | Mathematics (Maths) Class 10 PDF Download
Exercise 3.1
Choose the correct answer from the given four options:
Q.1. Graphically, the pair of equations
6x – 3y + 10 = 0
2x – y + 9 = 0
represents two lines which are
(a) Intersecting at exactly one point.
(b) Intersecting at exactly two points.
(c) Coincident
(d) parallel.
Correct Answer is option (d)
Given, the linear equations are 6x − 3y + 10 = 0 and 2x − y + 9 = 0
On comparing with a1x + b1y = c1 and a2x + b2y = c2,we get:
So, a1 = 6, b1 = −3, c1 = 10
a2 = 2, b2 = −1, c2 = 9
Therefore, the lines representing the given equations are parallel.
OR
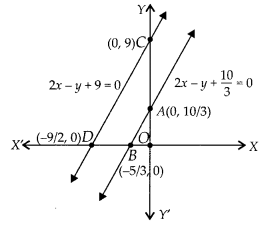
The given equations are 6x – 3y + 10 = 0
⇒ 2x – y + 10/3 = 0 …(i)
and 2x – y + 9 = 0 … (ii)
Now, table for 2x – y + 10/3 = 0,
Q.2. The pair of equations x + 2y + 5 = 0 and –3x – 6y + 1 = 0 have
(a) a unique solution
(b) exactly two solutions
(c) infinitely many solutions
(d) no solution
Correct Answer is option (d)
From the equations
x + 2y + 5=0 and −3x − 6y + 1= 0The above equations are of the form a1x + b1y + c1=0and a2x + b2y + c2 = 0
Therefore, the pair of equations x + 2y + 5= 0 and −3x − 6y + 1 = 0 have no solution.
Q.3. If a pair of linear equations is consistent, then the lines will be
(a) parallel
(b) always coincident
(c) intersecting or coincident
(d) always intersecting
If a pair of linear equations is consistent, then it has unique solutions and infinite solutions.
If
then the graph will be a pair of lines intersecting at a unique point, which is the solution of the pair of equations.
If
then the graph will be a pair of coincident lines. Each point on the lines will be a solution, and so the pair of equations will have infinitely many solutions
Q.4. The pair of equations y = 0 and y = –7 has
(a) one solution
(b) two solutions
(c) infinitely many solutions
(d) no solution
Correct Answer is option (d)
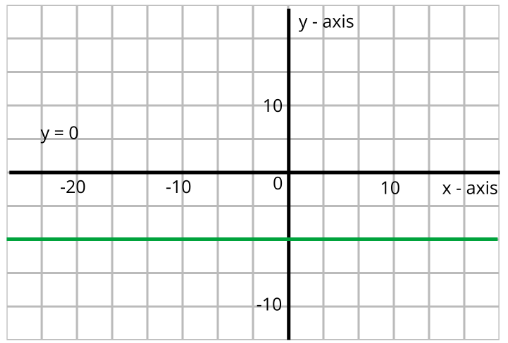
Given the pair of equations are y = 0 and y = −7
Graph the pair of equations y = 0 and y = −7
From the above graph y = 0 and y = −7 are parallel, so the pair of equations y = 0and y = −7 have no solutions.
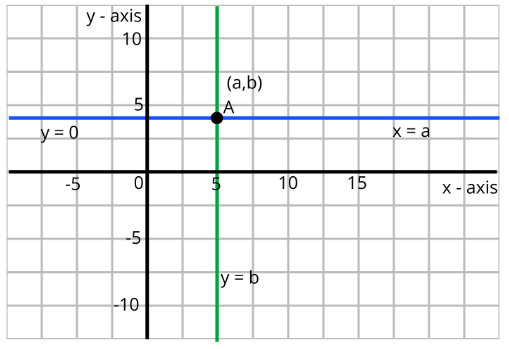
Q.5. The pair of equations x = a and y = b graphically represents lines which are
(a) parallel
(b) intersecting at (b, a)
(c) coincident
(d) intersecting at (a, b)
Correct Answer is option (d)
Given pair of equations x = a and y = b
From the graph, the lines are x = a and y = b intersecting lines and they intersect at the point (a, b).
Q.6. For what value of k, do the equations 3x – y + 8 = 0 and 6x – ky = –16 represent coincident lines?
(a) 1/2
(b) -(1/2)
(c) 2
(d) -2
Correct Answer is option (c)
Given equations 3x − y + 8 = 0 and 6x − ky = −16
The above equations are of the form a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0
So, a1 = 3, b1 = −1, c1 = 8 and a2 = 6, b2 = −k, c2=16
since, lines are coincident
therefore,
Q.7. If the lines given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, then the value of k is
(a) (-5)/4
(b) 2/5
(c) 15/4
(d) 3/2
Correct Answer is option (c)
Given lines 3x + 2ky − 2 = 0 and 2x + 5y − 1 = 0 are parallel.
On comparing the linear equations with a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, we get:
a1 = 3, b1 = 2k, c1 = −2 and a2 = 2, b2=5, c2 = −1
Since, the lines are parallel.
Q.8. The value of c for which the pair of equations cx – y = 2 and 6x – 2y = 3 will have infinitely many solutions is
(a) 3
(b) -3
(c) -12
(d) no value
Correct Answer is option (d)
Given a pair of equations cx − y = 2 and 6x − 2y = 3 will have infinitely many solutions.
On comparing the linear equations with a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, we get:
a1 = c, b1 = −1, c1 = −2 and a2 = 6, b2 = −2, c2 = −3.
since,
Then,
c = 3 and c = 4
Here, the value of chas no value because cvalue has different values.
Q.9. One equation of a pair of dependent linear equations is –5x + 7y = 2. The second equation can be
(a) 10x + 14y + 4 = 0
(b) –10x – 14y + 4 = 0
(c) –10x + 14y + 4 = 0
(d) 10x – 14y = –4
Correct Answer is option (d)
Given pair of dependent linear equation is −5x + 7y − 2
From the equation −5x + 7y − 2
a1 = −5, b1 = 7, c1 = −2
Then, from the dependent linear condition
−5a2 = 7b2=−2 c2 = 1k
⇒ a2 = −5k, b2 = 7k, c2 = −2k
where, k is an arbitrary constant.
Substitutingk=2, then
a2 = −10, b2 = 14 and c2 = −4
The required second line becomes a2x + b2y + c2 = 0
⇒−10x + 14y − 4 = 0
⇒10x − 14y + 4 = 0
Q.10. A pair of linear equations which has a unique solution x = 2, y = –3 is
(a) x + y = –1 and 2x – 3y = –5
(b) 2x + 5y = –11 and 4x + 10y = –22
(c) 2x – y = 1 and 3 x + 2y = 0
(d) x – 4y –14 = 0 and 5x – y – 13 = 0
Correct Answer is option (b) & (d)
The pair of linear equations which have a unique solution x = 2, y = −3 .
If x = 2 and y = −3 substitute in all equations it must satisfy the L.H.S = R.H.S
Substitute x = 2,y = −3 in option (A)
x + y = −1;2x − 3y = −5
2 − 3 = −1; 2(2) − 3(−3) = −5
−1 = −1; 13 = −5
True; False
Substitute x = 2, y = −3 in option (B)
2x + 5y = −11; 4x + 10y = −22
2(2) + 5(−3) = −11 ; 4(2) + 10(−3) = −22
4 − 15 = −11; 8 − 30 = −22
−11 = −11 True ; −22 = −22 True
Substitute x = 2, y = −3 in option (C)
2x − y = 1; 3x + 2y = 0
2(2) − (−3) = 1;3(2) + 3(−3) = 0
4 + 3 = 1;6 − 6 = 0
7 = 1(False) ;0 = 0(True)
Substitute x = 2, y = −3 in option (D)
x − 4y − 14 = 0; 5x − y − 13 = 0
2 − 4(−3) − 14 = 0; 5(2) − (−3) − 13 = 0
2 + 12 − 14 = 0; 10 + 3 − 13 = 0
0 = 0 (True) ;13 − 13 = 0
0 = 0 (True);0 = 0 (True)
By substituting the values in x = 2, y = −3 in options(A), (B), (C) and (D) , two options (B), (D) satisfy the L.H.S = R.H.S
Q.11. If x = a, y = b is the solution of the equations x – y = 2 and x + y = 4, then the values of a and b are, respectively
(a) 3 and 5
(b) 5 and 3
(c) 3 and 1
(d) –1 and –3
Correct Answer is option (c)
Given x = a and y = b
Substitute the values of x = a, y = b in given equations x − y = 2 and x + y = 4, then
⇒ a− b = 2………..(1)
⇒ a + b = 4…………(2)
Add equations (1) and (2)
2a = 6
⇒ a = 6/2
⇒ a = 3
Substitute the value of a in equation (1)
⇒ 3 − b = 2
⇒ −b = 2 − 3
⇒ b = 1
Therefore, the value of a = 3 and b = 1
Q.12. Aruna has only Re 1 and Rs 2 coins with her. If the total number of coins that she has is 50 and the amount of money with her is Rs 75, then the number of Re 1 and Rs 2 coins are, respectively
(a) 35 and 15
(b) 35 and 20
(c) 15 and 35
(d) 25 and 25
Correct Answer is option (d)
Consider,
x: Aruna has only Rs coins with her.
y: Aruna has only Rs 1 coins with her.
From the question,
The total number of coins that she has is 50
Total number of coins
= x + y = 50 …………. (i)Also, Amount of money with her
= (Number of Rs1 × coin1) + ( Number of Rs2 × coin2)
= x + 2y = 75
Subtract Eq. (i) from Eq. (ii), then
(x + 2y)−(x + y) = (75 − 50)
So, y = 25
Substituting y= 25 in eq(i)
⇒ x + 25 = 50
⇒ x = 50 − 25
⇒ x = 25
Therefore, Aruna has 25 Re 1 coins and 25 Rs 2 coins.
Q.13. The father’s age is six times his son’s age. Four years hence, the age of the father will be four times his son’s age. The present ages, in years, of the son and the father are, respectively
(a) 4 and 24
(b) 5 and 30
(c) 6 and 36
(d) 3 and 24
Correct Answer is option (c)
Consider the present age of father be ' x ' year and the present age of son be 'y' year .
From the given question, Four years hence, the age of the father will be four times his son's age then
(x + 4) = 4(y + 4)
x + 4 = 4y + 16
x − 4y − 12 = 0 …..(i)
And the father's age is six times his son's age,
x = 6y ………(ii)
Substituting the value of Eq. (ii) in Eq. (i) then
6y − 4y − 12 = 0
2y = 12
Therefore, y = 6
Substituting y = 6 in eq (ii),
x = 6(6)
x = 36
Therefore, the present age of the father is 36 years and the age of the son is years.
Exercise 3.2
Q.1. Do the following pair of linear equations have no solution? Justify your answer.
(i) 2x + 4y = 3
12y + 6x = 6
(ii) x = 2y
y = 2x
(iii) 3x + y – 3 = 0
2x + 2/3y = 2
The Condition for no solution = a1/a2 = b1/b2 ≠ c1/c2 (parallel lines)
(i) Yes.
Given pair of equations are,
2x + 4y – 3 = 0 and 6x + 12y – 6 = 0
Comparing the equations with ax+ by +c = 0;
We get,
a1 = 2, b1 = 4, c1 = – 3;
a2 = 6, b2 = 12, c2 = – 6;
a1 /a2 = 2/6 = 1/3
b1 /b2 = 4/12 = 1/3
c1 /c2 = – 3/ – 6 = ½
Here, a1/a2 = b1/b2 ≠ c1/c2, i.e parallel lines
Hence, the given pair of linear equations has no solution.
(ii) No.
Given pair of equations,
x = 2y or x – 2y = 0
y = 2x or 2x – y = 0;
Comparing the equations with ax+ by +c = 0;
We get,
a1 = 1, b1 = – 2, c1 = 0;
a2 = 2, b2 = – 1, c2 = 0;
a1 /a2 = ½
b1 /b2 = -2/-1 = 2
Here, a1/a2 ≠ b1/b2.
Hence, the given pair of linear equations has unique solution.
(iii) No.
Given pair of equations,
3x + y – 3 = 0
2x + 2/3 y = 2
Comparing the equations with ax+ by +c = 0;
We get,
a1 = 3, b1 = 1, c1 = – 3;
a2 = 2, b2 = 2/3, c2 = – 2;
a1 /a2 = 2/6 = 3/2
b1 /b2 = 4/12 = 3/2
c1 /c2 = – 3/-2 = 3/2
Here, a1/a2 = b1/b2 = c1/c2, i.e coincident lines
Q.2. Do the following equations represent a pair of coincident lines? Justify your answer.
(i) 3x + 1/7y = 3
7x + 3y = 7
(ii) –2x – 3y = 1
6y + 4x = – 2
(iii) x/2 + y + 2/5 = 0
4x + 8y + 5/16 = 0
Condition for coincident lines,
a1/a2 = b1/b2 = c1/c2;
(i) No.
Given pair of linear equations are:
3x + 1/7y = 3
7x + 3y = 7
Comparing the above equations with ax + by + c = 0;
Here, a1 = 3, b1 = 1/7, c1 = – 3;
And a2 = 7, b2 = 3, c2 = – 7;
a1 /a2 = 3/7
b1 /b2 = 1/21
c1 /c2 = – 3/ – 7 = 3/7
Here, a1/a2 ≠ b1/b2.
Hence, the given pair of linear equations has unique solution.
(ii) Yes,
Given pair of linear equations.
– 2x – 3y – 1 = 0 and 4x + 6y + 2 = 0;
Comparing the above equations with ax + by + c = 0;
Here, a1 = – 2, b1 = – 3, c1 = – 1;
And a2 = 4, b2 = 6, c2 = 2;
a1 /a2 = – 2/4 = – ½
b1 /b2 = – 3/6 = – ½
c1 /c2 = – ½
Here, a1/a2 = b1/b2 = c1/c2, i.e. coincident lines
Hence, the given pair of linear equations is coincident.
(iii) No,
Given pair of linear equations are
x/2 + y + 2/5 = 0
4x + 8y + 5/16 = 0
Comparing the above equations with ax + by + c = 0;
Here, a1 = ½, b1 = 1, c1 = 2/5;
And a2 = 4, b2 = 8, c2 = 5/16;
a1 /a2 = 1/8
b1 /b2 = 1/8
c1 /c2 = 32/25
Here, a1/a2 = b1/b2 ≠ c1/c2, i.e. parallel lines
Hence, the given pair of linear equations has no solution.
Q.3. Are the following pair of linear equations consistent? Justify your answer.
(i) –3x– 4y = 12
4y + 3x = 12
(ii) (3/5)x – y = ½
(1/5)x – 3y= 1/6
(iii) 2ax + by = a
1. ax + 2by – 2a = 0; a, b ≠ 0
(iv) x + 3y = 11
2 (2x + 6y) = 22
Conditions for pair of linear equations to be consistent are:
a1/a2 ≠ b1/b2. [unique solution]
a1/a2 = b1/b2 = c1/c2 [coincident or infinitely many solutions]
(i) No.
The given pair of linear equations
– 3x – 4y – 12 = 0 and 4y + 3x – 12 = 0
Comparing the above equations with ax + by + c = 0;
We get,
a1 = – 3, b1 = – 4, c1 = – 12;
a2 = 3, b2 = 4, c2 = – 12;
a1 /a2 = – 3/3 = – 1
b1 /b2 = – 4/4 = – 1
c1 /c2 = – 12/ – 12 = 1
Here, a1/a2 = b1/b2 ≠ c1/c2
Hence, the pair of linear equations has no solution, i.e., inconsistent.
(ii) Yes.
The given pair of linear equations
(3/5)x – y = ½
(1/5)x – 3y= 1/6
Comparing the above equations with ax + by + c = 0;
We get,
a1 = 3/5, b1 = – 1, c1 = – ½;
a2 = 1/5, b2 = 3, c2 = – 1/6;
a1 /a2 = 3
b1 /b2 = – 1/ – 3 = 1/3
c1 /c2 = 3
Here, a1/a2 ≠ b1/b2.
Hence, the given pair of linear equations has unique solution, i.e., consistent.
(iii) Yes.
The given pair of linear equations –
2ax + by –a = 0 and 4ax + 2by – 2a = 0
Comparing the above equations with ax + by + c = 0;
We get,
a1 = 2a, b1 = b, c1 = – a;
a2 = 4a, b2 = 2b, c2 = – 2a;
a1 /a2 = ½
b1 /b2 = ½
c1 /c2 = ½
Here, a1/a2 = b1/b2 = c1/c2
Hence, the given pair of linear equations has infinitely many solutions, i.e., consistent
(iv) No.The given pair of linear equations
x + 3y = 11 and 2x + 6y = 11
Comparing the above equations with ax + by + c = 0;
We get,
a1 = 1, b1 = 3, c1 = 11
a2 = 2, b2 = 6, c2 = 11
a1 /a2 = ½
b1 /b2 = ½
c1 /c2 = 1
Here, a1/a2 = b1/b2 ≠ c1/c2.
Hence, the given pair of linear equations has no solution.
Q.4. For the pair of equations
λx + 3y = –7
2x + 6y = 14
to have infinitely many solutions, the value of λ should be 1. Is the statement true?
Give reasons.
No, the given pair of linear equations
λx + 3y + 7 = 0 and 2x + 6y – 14 = 0
Here, a1 = λ, b1 = 3 c1 =7,
a2 = 2, b2 = 6, c2 = –14
Ifthen system has infinitely many solutions.
⇒ λ = 1 And
⇒ λ = - 1Hence, λ = –1 does not have a unique value. ‘
So, for no value of λ the given pair of linear equations has infinitely many solutions.
Q.5. For all real values of c, the pair of equations x – 2y = 8, 5x – 10y = c have a unique solution. Justify whether it is true or false.
The statement for all real values of c, the pair of equations x − 2y = 8and 5x−10y=c have a unique solution is true .
Given the pair of equations x − 2y = 8 and 5x − 10y = c
The above equations are of the form a1x + b1y = c1 = 0 and a2x + b2y = c2
So, a1 =1, b1 = −2, c1 = 8 and a2=5, b2 = −10, c2 = c
From the above a1 / a2 ≠ b1 / b2, system has unique solution.
The statement that for all real values ofc, the pair of equations x − 2y = 8 and 5x−10y = c have a unique solution is true .
Q.6. The line represented by x = 7 is parallel to the x–axis. Justify whether the statement is true or not.
The line represented by x = 7 is parallel to the x -axis.
In the given statement the line represented by x = 7 is parallel to the x -axis is not true.
Exercise 3.3
Q.1. For which value(s) of λ, do the pair of linear equations
λx + y = λ2 and x + λy = 1 have
(i) no solution?
(ii) infinitely many solutions?
(iii) a unique solution?
The given pair of linear equations is
λx + y = λ2 and x + λy = 1
a1 = λ, b1= 1, c1 = – λ2
a2 = 1, b2 = λ, c2= -1
The given equations are;
λ x + y – λ2 = 0
x + λ y – 1 = 0
Comparing the above equations with ax + by + c = 0;
We get,
a1 = λ, b1 = 1, c1 = – λ 2;
a2 = 1, b2 = λ, c2 = – 1;
a1 /a2 = λ/1
b1 /b2 = 1/λ
c1 /c2 = λ2
(i) For no solution,
a1/a2 = b1/b2≠ c1/c2
i.e. λ = 1/ λ ≠ λ2
so, λ 2 = 1;
and λ 2 ≠ λ
Here, we take only λ = – 1,
Since the system of linear equations has no solution.
(ii) For infinitely many solutions,
a1/a2 = b1/b2 = c1/c2
i.e. λ = 1/ λ = λ2
so λ = 1/ λ gives λ = + 1;
λ = λ 2 gives λ = 1,0;
Hence satisfying both the equations
λ = 1 is the answer.
(iii) For a unique solution,
a1/a2 ≠ b1/b2
so λ ≠1/ λ
hence, λ2 ≠ 1;
λ ≠ + 1;
So, all real values of λ except +1
Q.2. For which value(s) of k will the pair of equations
kx + 3y = k – 3
12x + ky = k
have no solution?
The given pair of linear equations is
kx + 3y = k – 3 …(i)
12x + ky = k …(ii)
On comparing the equations (i) and (ii) with ax + by = c = 0,
We get,
a1 = k, b1 = 3, c1 = -(k – 3)
a2 = 12, b2 = k, c2 = – k
Then,
a1 /a2 = k/12
b1 /b2 = 3/k
c1 /c2 = (k-3)/k
For no solution of the pair of linear equations,
a1/a2 = b1/b2≠ c1/c2
k/12 = 3/k ≠ (k-3)/k
Taking first two parts, we get
k/12 = 3/k
k2 = 36
k = + 6
Taking last two parts, we get
3/k ≠ (k-3)/k
3k ≠ k(k – 3)
k2 – 6k ≠ 0
so, k ≠ 0, 6
Therefore, value of k for which the given pair of linear equations has no solution is k = – 6.
Q.3. For which values of a and b, will the following pair of linear equations have infinitely many solutions?
x + 2y = 1
(a – b)x + (a + b)y = a + b – 2
The given pair of linear equations are:
x + 2y = 1 …(i)
(a - b)x + (a + b)y = a + b – 2 …(ii)
On comparing with ax + by = c = 0 we get
a1 = 1, b1 = 2, c1 = – 1
a2 = (a – b), b2 = (a + b), c2 = – (a + b – 2)
a1 /a2 = 1/(a - b)
b1 /b2 = 2/(a + b)
c1 /c2 = 1/(a + b - 2)
For infinitely many solutions of the, pair of linear equations,
a1/a2 = b1/b2=c1/c2(coincident lines)
so, 1/(a - b) = 2/ (a + b) = 1/(a + b - 2)
Taking first two parts,
1/(a-b) = 2/ (a+b)
a + b = 2(a – b)
a = 3b …(iii)
Taking last two parts,
2/ (a + b) = 1/(a + b - 2)
2(a + b – 2) = (a + b)
a + b = 4 …(iv)
Now, put the value of a from Eq. (iii) in Eq. (iv), we get
3b + b = 4
4b = 4
b = 1
Put the value of b in Eq. (iii), we get
a = 3
So, the values (a, b) = (3, 1) satisfies all the parts. Hence, required values of a and b are 3 and 1 respectively for which the given pair of linear equations has infinitely many solutions.
Q.4. Find the value(s) of p in (i) to (iv) and p and q in (v) for the following pair of equations:
(i) 3x – y – 5 = 0 and 6x – 2y – p = 0, if the lines represented by these equations are parallel.
Given pair of linear equations is
3x – y – 5 = 0 …(i)
6x – 2y – p = 0 …(ii)
On comparing with ax + by + c = 0 we get
We get,
a1 = 3, b1 = – 1, c1 = – 5;
a2 = 6, b2 = – 2, c2 = – p;
a1 /a2 = 3/6 = ½
b1 /b2 = ½
c1 /c2 = 5/p
Since, the lines represented by these equations are parallel, then
a1/a2 = b1/b2 ≠ c1/c2
Taking last two parts, we get ½ ≠ 5/p
So, p ≠ 10
Hence, the given pair of linear equations are parallel for all real values of p except 10.
(ii) – x + py = 1 and px – y = 1, if the pair of equations has no solution.
Given pair of linear equations is
– x + py = 1 …(i)
px – y – 1 = 0 …(ii)
On comparing with ax + by + c = 0,
We get,
a1 = -1, b1 = p, c1 =- 1;
a2 = p, b2 = – 1, c2 =- 1;
a1 /a2 = -1/p
b1 /b2 = – p
c1 /c2 = 1
Since, the lines equations has no solution i.e., both lines are parallel to each other.
a1/a2 = b1/b2≠ c1/c2
-1/p = – p ≠ 1
Taking last two parts, we get
p ≠ -1
Taking first two parts, we get
p2 = 1
p = + 1
Hence, the given pair of linear equations has no solution for p = 1.
(iii) – 3x + 5y = 7 and 2px – 3y = 1, if the lines represented by these equations are intersecting at a unique point.
Given, pair of linear equations is
– 3x + 5y = 7
2px – 3y = 1
On comparing with ax + by + c = 0, we get
Here, a1 = -3, b1 = 5, c1 = – 7;
And a2 = 2p, b2 = – 3, c2 = – 1;
a1 /a2 = -3/ 2p
b1 /b2 = – 5/3
c1 /c2 = 7
Since, the lines are intersecting at a unique point i.e., it has a unique solution
a1/a2 ≠ b1/b2
-3/2p ≠ -5/3
p ≠ 9/10
Hence, the lines represented by these equations are intersecting at a unique point for all real values of p except 9/10
(iv) 2x + 3y – 5 = 0 and px – 6y – 8 = 0, if the pair of equations has a unique solution.
Given, pair of linear equations is
2x + 3y – 5 = 0
px – 6y – 8 = 0
On comparing with ax + by + c = 0 we get
Here, a1 = 2, b1 = 3, c1 = – 5;
And a2 = p, b2 = – 6, c2 = – 8;
a1 /a2 = 2/p
b1 /b2 = – 3/6 = – ½
c1 /c2 = 5/8
Since, the pair of linear equations has a unique solution.
a1/a2 ≠ b1/b2
so 2/p ≠ – ½
p ≠ – 4
Hence, the pair of linear equations has a unique solution for all values of p except – 4.
(v) 2x + 3y = 7 and 2px + py = 28 – qy, if the pair of equations have infinitely many solutions.
Given pair of linear equations is
2x + 3y = 7
2px + py = 28 – qy
or 2px + (p + q)y – 28 = 0
On comparing with ax + by + c = 0,
We get,
Here, a1 = 2, b1 = 3, c1 = – 7;
And a2 = 2p, b2 = (p + q), c2 = – 28;
a1/a2 = 2/2p
b1/b2 = 3/ (p + q)
c1/c2 = ¼
Since, the pair of equations has infinitely many solutions i.e., both lines are coincident.
a1/a2 = b1/b2 = c1/c2
1/p = 3/(p+q) = ¼
Taking first and third parts, we get
p = 4
Again, taking last two parts, we get
3/(p+q) = ¼
p + q = 12
Since p = 4
So, q = 8
Here, we see that the values of p = 4 and q = 8 satisfies all three parts.
Hence, the pair of equations has infinitely many solutions for all values of p = 4 and q = 8.
Q.5. Two straight paths are represented by the equations x – 3y = 2 and –2x + 6y = 5. Check whether the paths cross each other or not.
Given linear equations are
x – 3y – 2 = 0 …(i)
-2x + 6y – 5 = 0 …(ii)
On comparing with ax + by c = 0,
We get
a1 = 1, b1 = -3, c1 = - 2;
a2 = -2, b2 = 6, c2 = - 5;
a1/a2 = – ½
b1/b2 = – 3/6 = – ½
c1/c2 = 2/5
i.e., a1/a2 = b1/b2 ≠ c1/c2 [parallel lines]
Hence, two straight paths represented by the given equations never cross each other, because they are parallel to each other.
Q.6. Write a pair of linear equations which has the unique solution x = – 1, y =3. How many such pairs can you write?
Condition for the pair of system to have unique solution
a1/a2 ≠ b1/b2
Let the equations be,
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
Since, x = – 1 and y = 3 is the unique solution of these two equations, then
It must satisfy the equations –
a1(-1) + b1(3) + c1 = 0
– a1 + 3b1 + c1 = 0 …(i)
and a2(- 1) + b2(3) + c2 = 0
– a2 + 3b2 + c2 = 0 …(ii)
Since for the different values of a1, b1, c1 and a2, b2, c2 satisfy the Eqs. (i) and (ii).Hence, infinitely many pairs of linear equations are possible.
Q.7. If 2x + y = 23 and 4x – y = 19, find the values of 5y – 2x and y/x – 2.
Given equations are
2x + y = 23 …(i)
4x – y = 19 …(ii)
On adding both equations, we get
6x = 42
So, x = 7
Put the value of x in Eq. (i), we get
2(7) + y = 23
y = 23 – 14
so, y = 9
Hence 5y – 2x = 5(9) – 2(7) = 45 – 14 = 31
y/x – 2 = 9/7 -2 = -5/7
Hence, the values of (5y – 2x) and y/x – 2 are 31 and -5/7 respectively.
Q.8. Find the values of x and y in the following rectangle [see Fig. 3.2].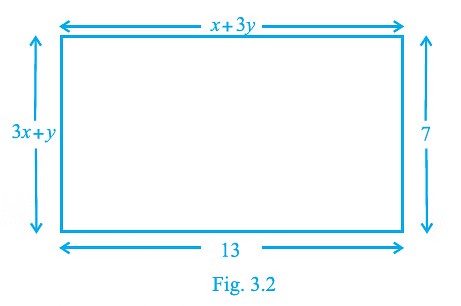
Using property of rectangle,
We know that,
Lengths are equal,i.e., CD = AB
Hence, x + 3y = 13 …(i)
Breadth are equal,
i.e., AD = BC
Hence, 3x + y = 7 …(ii)
On multiplying Eq. (ii) by 3 and then subtracting Eq. (i),
We get,
8x = 8
So, x = 1
On substituting x = 1 in Eq. (i),
We get,
y = 4
Therefore, the required values of x and y are 1 and 4, respectively.
Q.9. Solve the following pairs of linear equations :
(i)
Ans. We have x + y = 3.3 ....(i)
On multiplying eqn. (i) by 20 we get20x + 20y = 66
From eqn. (ii) we have
−3x + 2y = 0.6
On multiplying it by (−10) we get
30x − 20y = −6 ...(iii)
Now adding (iii) and (iv) we getNow 10(1.2) 10y = 33 [ from (i) ]⇒ 12 + 10y = 33
⇒ 10y = 33 − 12
⇒ y = (21/10) ⇒ y = 2.1
∴ The solution of the given system of equation is x = 1.2 and y = 2.1
(ii)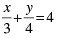

4x + 3y = 48 ...(iii)20x − 3y = 96 ...(iv)
24x = 144 [ adding equations iii and iv]
⇒ x = (144/24) ⇒ x = 6
Now , 4x + 3y = 48 [from (iii)]
On putting the value of x = 6 we have
4(6) + 3y = 48
⇒ 3y = 48 − 24
⇒ 3y = 24
⇒ y= 24/3 ⇒ y = 8
So the solution of the given equations is x = 6 and y = 8.
(iii) 4x + (6/y) = 15
6x - (8/y) = 14, y ≠ 0
The equation 4x+ (6/y) =15 can be solved as:
4x+ (6/y) = 15
⇒ (4xy+ 6)/y = 15
⇒ 4xy + 6 = 15y ...(1)
The equation 6x - (8/y) = 14 can be solved as:
6x - (8/y) = 14
⇒ (6xy - 8)/y = 14
⇒ 6xy − 8 = 14y ...(2)
Multiply the equation 1 by 3 and equation 2 by 2. Then we get the equations:
12xy + 18 = 45y ...(3)
12xy − 16 = 28y ...(4)
Subtract Equation 4 from equation 3 to eliminate xy, because the coefficients of xy are same. So, we get
(12xy − 12xy) + (18 + 16) = 45y − 28y
i.e. 17y = 34
i.e. y = 2
Substituting this value of y in the equation 1, we get
8x + 6 = 30
i.e. 8x = 30 − 6 = 24
i.e. x = 3
Hence, the solution of the equations is x = 3, y=2.
(iv) (1/2x) - (1/y) = -1
(1/x) + (1/2y) = 8, x, y ≠ 0
(1/2x) - (1-y) = -1
(y - 2x)/(2xy) = -1
y - 2x = -2xy
2x - y = 2xy ....(1)
(1/x) + (1/2y) = 8
(2y + x)/(2xy) = 8
2y + x = 16xy
x + 2y = 16xy ....(2)y = 1/4from eq. (1) 2x - (1/4) = 2xy
8x - 1 = 8 x (y/4)
6x = 1
x = 1/6
(v) 43x + 67y = – 24
67x + 43y = 24
Given,
43x + 67y = −24 ...(i)
67x + 43y = 24 ...(ii)
On multiplying (i) by 67 and (ii) by 43, we get
∴ y = −1 On putting y=−1 in (i), we get
43x − 67 = −24 ⇒ 43x = 43 ⇒ x = 1
∴ x = 1, y = −1
(vi) (x/a) + (y/b) = a + b
(x/(a2)) + (y/(b2) = 2, a, b ≠ 0
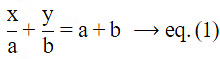
By multiplying eq.(1) by (1/a), we get
On subtracting eq. (3) from (2), we get
⇒ y = b2
On putting the value of y in eq. (1), we getHence, x = a2 & y = b2
(vii) 2xy/(x + y) = 3/2
xy/(2x - y) = (-3)/10, (x + y ≠ 0, 2x – y ≠ 0)
Then, equations (1) and (2) become
⇒ 3u + 3v = 4 and −3u + 6v = −10Adding, we have
9v = −6Substituting y = −(3/2) in (1), we have
⇒ x = (1/2)Hence, x = (1/2) and y = -(3/2)
Q.10. Find the solution of the pair of equations 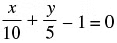 and
and 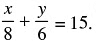 Hence, find λ, if y = λx + 5.
Hence, find λ, if y = λx + 5.
Given equations are
And
⇒ 4x = +340now 2x + 4y = 20 [ from (iii) ]
⇒ x + 2y =10
⇒ 340 + 2y =10[Rs x = 340]
⇒ 2y = 10 − 340
⇒ 2y = −330and x = 340Now , y = λx + 5 [given]
⇒ −165 = λ(340) + 5[Rs y = −165 and x = 340]
⇒ −λ(340) = 170hence the solution of the given pair of equation is x = 340, y = −165 and λ = -(1/2).
Q.11. By the graphical method, find whether the following pair of equations are consistent or not. If consistent, solve them.
(i) 3x + y + 4 = 0
6x – 2y + 4 = 0
From the above question, we have the equation as,
3x + y + 4 = 0 ...(1)
6x - 2y + 4 = 0 ...(2)
Comparing with the general form of straight line ax + by + c = 0, we get,
a1 = 3, b1 = l c1 = 4
a2 = 6, b2 = -2 c2 = 4
a1/a2 = 1/2;
b1/b2 = 1/-2;
c1/c2 = 1.
a1/a2 ≠ b1/b2.
Hence, the given pair of linear equations are intersecting at one point and these lines have a unique solution.
Therefore, the given pairs of linear equations are consistent.
Let us graphically illustrate this.
We have, 3x + y + 4 = 0.
y = -4 - 3x.6x - 2y + 4 = 02y = 6x + 4
y = 3x + 2Plotting the points B(0, -4) and A(-2, 2), we get the straight line AB.Plotting the points Q(0,2) and P(1, 5), we get the straight line PQ.
The lines AB and PQ intersect at C (-1, -1).Therefore, the above pairs are consistent.
(ii) x – 2y = 6
3x – 6 y = 0
Given equations are,
x − 2y = 6 ...(i)
3x − 6y = 0 ...(ii)∴ System of equations is inconsistent , hence the lines represented by the given equations are parallel . so the given equations have no solutions.
(iii) x + y = 3
3x + 3y = 9
Table of eq. 1
Table of eq. 2The given equation can be written asx + y − 3 = 0 ...eq.1 and 3x + 3y − 9 = 0 ...eq.2
Here,Thus, the given pair of equation is consistent.
Q.12. Draw the graph of the pair of equations 2x + y = 4 and 2x – y = 4. Write the vertices of the triangle formed by these lines and the y-axis. Also find the area of this triangle.
2x + y = 4 ...(i)
⇒ y = 4 − 2x
If x = 0, y = 4 − 2(0) = 4 − 0 = 4
x = 1, y = 4 − 2(1) = 4 − 2 = 2
x = 2, y = 4 − 2(2) = 4 − 4 = 0(i) A B C −2
2x − y = 4 ...(ii)
⇒ y = 2x − 4
If x = 0, y = 2(0) − 4 = 0 − 4 = −4
x = 1, y = 2(1) − 4 = 2 − 4 =−2
x = 2, y = 2(2) − 4 = 4 − 4 = 0(ii) E F G H I
triangle formed by the lines with y -axis ΔAEC coordinates of vertices are A(0,4),E(0,−4) and C(2,0)
Area of ΔAEC= (1/2) Base × Altitude
= (1/2)AE x CO
= (1/2) x [4−(−4)] × (2−0)
= (1/2)× 8 × 2 = 8
∴ Area of ΔAEC= Square units.
Q.13. Write an equation of a line passing through the point representing solution of the pair of linear equations x + y = 2 and 2x – y = 1. How many such lines can we find?
Given pair of eq
x + y = 2 and 2x − y = 1
on solving both eq
x = 1, y = 1
Line passes through Point P(1,1)
Hence eq of line through P be
(y−1) = m(x−1)
or,
y = mx+(1−m)
Hence no of lines could be infinite
Q.14. If x + 1 is a factor of 2x3 + ax2 + 2bx + 1, then find the values of a and b given that 2a–3b = 4.
Since, x+1 is a factor of p(x) = 2x3 +ax2 +2bx + 1
Then, by factor theorem, p(−1) = 0
⇒ −2 + a − 2b + 1 = 0 ⇒ a−2b = 1 ...(i)
Also, 2a − 3b = 4 ...(ii)
On multiplying (i) by 2 and (ii) by 1, we get
2a − 4b = 2∴ b = 2On putting b = 2 in (i), we get
a − 2 × 2 = 1 ⇒ a = 5
∴ a = 5, b = 2
Q.15. The angles of a triangle are x, y and 40°. The difference between the two angles x and y is 30°. Find x and y.
Given, x, y and 40 are the angles of a triangle.
Therefore, x + y + 40 =180
x + y =140
The difference between the two angles x and y is 30.
Therefore, x − y = 30 ....(2)
Add equations (1) and (2), we get
2x = 170
⇒ x = 85
Substitute this value n equation (2), we get
85 − y = 30
⇒ y = 85 − 30
⇒ y = 55
Therefore, angles of a triangle are x = 85, y = 55 and 40.
Q.16. Two years ago, Salim was thrice as old as his daughter and six years later, he will be four years older than twice her age. How old are they now?
Step -1: Developing a linear equation in two variables in accordance to the Question
Let the age of salim = x
Let the age of his daughter = y
2 years ago their ages were, x - 2 and y - 2
Given relation, (x - 2) = 3(y-2)
⇒ x - 2 = 3y - 6
⇒ x - 3y + 4 = 0 ...(i)
6 years later their ages will be, x + 6 and y + 6
Given relation, x + 6 = 2(y + 6) + 4
⇒ x + 6 = 2y + 12 + 4
⇒ x - 2y - 10 = 0 ...(ii)
Step -2: Solving for x and y.
Subtracting equation (ii) from (i)
(x - 3y + 4) - (x - 2y - 10) = 0
⇒ x - 3y + 4 - x + 2y + 10 = 0
⇒ -y + 14 = 0
⇒ y = 14
Substituting y = 14 in equation (i)
x - 3(14) + 4 = 0
⇒ x = 42 - 4
⇒ x = 38
Hence, Salim’s present age is 38 years and his daughter’s age is 14 years. Thus, option D is the correct answer.
Q.17. The age of the father is twice the sum of the ages of his two children. After 20 years, his age will be equal to the sum of the ages of his children. Find the age of the father.
Let the age of father be x years
Let the age of one of his children be y years and age of other children be z years
From given information,
x = 2 × (y + z) ...(1)
After 20 years,
(x+20) = (y+20) + (z+20) ...(2)
Substituting value of (1) in (2), we get
2 × (y+z) +20 = y + z + 40
2y + 2z − y − z = 40 − 20
y + z = 20 ...(3)
Substituting value of (3) in (1), we get
x = 2 × (20)
⇒ x = 40
Age of father is 40 years.
Q.18. Two numbers are in the ratio 5 : 6. If 8 is subtracted from each of the numbers, the ratio becomes 4 : 5. Find the numbers.
Let the two numbers be x and y.
According to the question, (x/y) = (5/6)⇒ 5(x−8) = 4(y−8)⇒ 5x−40 = 4y−32
⇒ 5x−4y = 8…(ii)
On putting the value of y= (6x/5) in Eq. (ii), we get⇒ x = 40On putting the value of x=40 in Eq. (i), we get
Hence, the two numbers are 40 and 48 .
Q.19. There are some students in the two examination halls A and B. To make the number of students equal in each hall, 10 students are sent from A to B. But if 20 students are sent from B to A, the number of students in A becomes double the number of students in B. Find the number of students in the two halls.
Let the number of students in hall A be x and number of students in hall B be y.
If 10 students are send fro hall A to B, Then the number of students in hall A will be lessened by 10 and that of B will be increased by 10.
The same will happen when 20 students are send from hall B to hall A.
Therefore, according to first case, we have
x −10 = y + 10
x = y + 20 ...(1)
By second case, we have
x + 20 = 2(y−20)
x = 2y − 60 ...(2)
Solving (1) and (2), we get
y + 20 = 2y − 60
⇒ y = 80
Putting y = 80 in equation (1), we get
x = 80 + 20 = 100
So, the number of students in hall A = 100 and the number of students in hall B = 80.
Q.20. A shopkeeper gives books on rent for reading. She takes a fixed charge for the first two days, and an additional charge for each day thereafter. Latika paid Rs 22 for a book kept for six days, while Anand paid Rs 16 for the book kept for four days. Find the fixed charges and the charge for each extra day.
Let the fixed charge for two days be ₹x and the additional charge be ₹y per day
Step 1: Form the linear equation in two variables for Latika:
Number of days for Latika = 6 = 2 + 4
∴ Charges for Latika
= Fixed charge for two days + 4 x Additional charge per day
= x + 4y
And, it is given that Latika paid ₹22
∴ x + 4y = 22
x = 22 - 4y ...(i)
Step 2: Form the linear equation in two variables for Anand:
Number of days for Anand = 4 = 2 + 2
∴ Charge for Anand= Fixed charge for two days + 4 x Additional charge per day
= x + 2y
And, it is given that Anand paid ₹16
∴ x + 2y = 16
x = 16 - 2y ...(2)
Step 3: Solve for x and y:
On comparing equation (1) and (2), we get,
⇒ 22 - 4y =16 - 2y
2y = 6
= ₹3
Substituting y = 3 in equation (1), we get,
⇒ x = 22 - 4(3)
= 22 - 12 = ₹10
Therefore, a fixed charge for two days = ₹10 and an additional charge = ₹3 per day
Hence, the correct option is (b)
Q.21. In a competitive examination, one mark is awarded for each correct answer while (1/2) mark is deducted for every wrong answer. Jayanti answered 120 questions and got 90 marks. How many questions did she answer correctly?
Total number of questions = 120
Let x be the number of correct answers.
The number of wrong answers = (120 − x)
The marks scored by Jayanti is 90.
Now, according to the given question
Thus, Jayanti answered correctly 100 questions.
Q.22. The angles of a cyclic quadrilateral ABCD are
∠A = (6x + 10)°,
∠B = (5x)°
∠C = (x + y)°,
∠D = (3y – 10)°
Find x and y, and hence the values of the four angles.
As ABCD is a cyclic quadrilateral, we have ∠A + ∠C = 180° ...(The sum of the opposite angles of a cyclic quadrilateral =180°)
⇒ 6x + 10° + x + y = 180°
⇒ 7x + y = 170° ...(1)
and ∠B + ∠D = 180° ...(The sum of the opposite angles of a cyclic quadrilateral = 180°)
⇒ (3y − 10) + 5x = 180°
⇒ 3y + 5x = 190° ...(2).
Solving (1) and (2), we have,
x = 20°
y = 30°
A = 6x + 10 = 6 x 20° + 10° = 130°
B = 5x = 5 x 20° = 100°
C = x + y = 30° + 20° = 50°
D = 3y - 10 = 3 x 30 - 10 = 80°.
Therefore, option B is correct.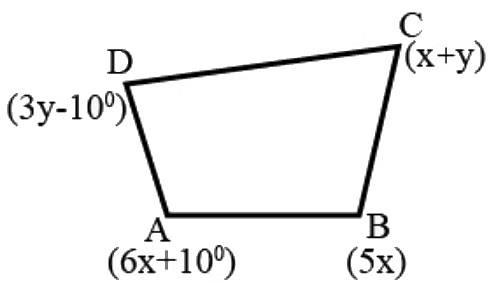
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Exemplar: Pair of Linear Equations in Two Variables- 1 - Mathematics (Maths) Class 10
| 1. What are the different methods to solve a pair of linear equations in two variables? |  |
| 2. How do you identify whether a pair of linear equations has a unique solution, infinitely many solutions, or no solution? |  |
| 3. Can you explain the graphical representation of linear equations? |  |
| 4. What is the importance of the coefficient matrix in solving linear equations? |  |
| 5. How can word problems be modeled as linear equations in two variables? |  |