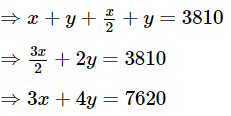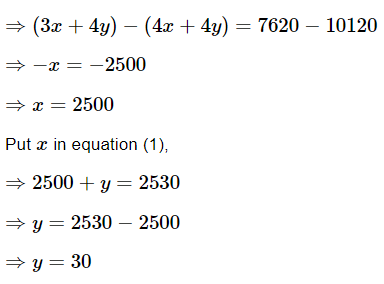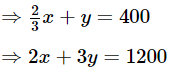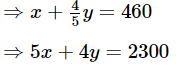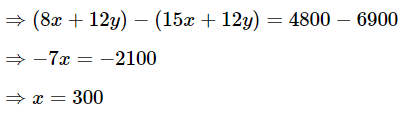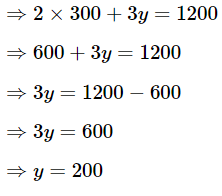NCERT Exemplar: Pair of Linear Equations in Two Variables- 2 | Mathematics (Maths) Class 10 PDF Download
Exercise 3.4
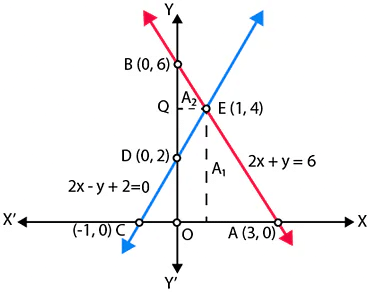
Q.1. Graphically, solve the following pair of equations:
2x + y = 6
2x – y + 2 = 0
Find the ratio of the areas of the two triangles formed by the lines representing these equations with the x-axis and the lines with the y-axis.
Given equations are 2x + y = 6 and 2x – y + 2 = 0
Table for equation 2x + y – 6 = 0, for x = 0, y = 6, for y = 0, x = 3.
x
0
3
y
6
0
Table for equation 2x – y + 2 = 0, for x = 0, y = 2, for y = 0,x = – 1
x
0
-1
y
2
0
Let A1 and A2 represent the areas of triangles ACE and BDE respectively.
Let, Area of triangle formed with x -axis = A1
A1 = Area of △ACE = ½ × AC × PE
A1 = ½ × 4 × 4 = 8
And Area of triangle formed with y – axis = A2
A1 = Area of △BDE = ½ × BD × QE
A1 = ½ × 4 × 1 = 2
A1 : A2 = 8:2 = 4:1
Hence, the pair of equations intersect graphically at point E(1, 4)
i.e., x = 1 and y = 4.
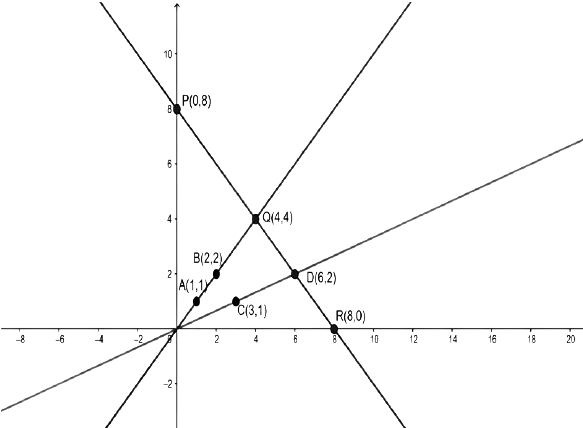
Q.2. Determine, graphically, the vertices of the triangle formed by the lines
y = x, 3y = x, x + y = 8
Given linear equations are
y = x …(i)
3y = x …(ii)
and x + y = 8 …(iii)
Table for line y = x,
x
0
1
2
y
0
1
2
Table for line x = 3y,
x
0
3
6
y
0
1
2
Table for line x + y = 8
x
0
4
8
y
8
4
0
Graph of the lines is as follows:
The lines y = x and 3y = x intersect the line x + y = 8 at Q and D.
Thus,ΔOQD is formed by these lines.
Therefore, the vertices of △OQD are O(0, 0),Q(4, 4)and(6, 2).
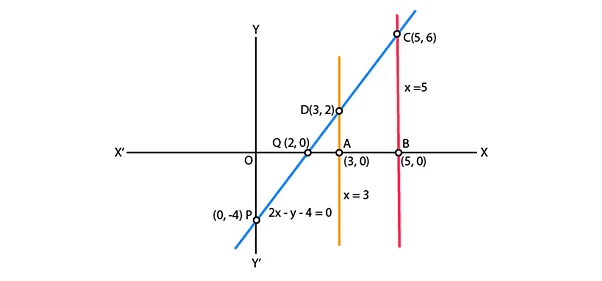
Q.3. Draw the graphs of the equations x = 3, x = 5 and 2x – y – 4 = 0. Also find the area of the quadrilateral formed by the lines and the x–axis.
Given equation of lines x = 3, x = 5 and 2x - y - 4 = 0.
Table for line 2x – y – 4 = 0
x
0
2
y
-4
0
Plotting the graph, we get,
From the graph, ABCD is the quadrilateral formed by the given lines and x-axis.
AB = OB - OA = 5 - 3 = 2, AD = 2 and BC = 6
Area of Quadrileral ABCD = ½ × (distance between parallel lines x sum of parallel sides) = ½ × (AB) × (AD + BC)
= 1/2 x 2 x 8
= 8 sq units
Q.4. The cost of 4 pens and 4 pencil boxes is Rs 100. Three times the cost of a pen is Rs 15 more than the cost of a pencil box. Form the pair of linear equations for the above situation. Find the cost of a pen and a pencil box.
Let the cost of one pen be x and the cost of one pencil box be y .
⇒ 4x + 4y = 100
⇒ x + y = 25.....(1)
and 3x = y + 15
⇒ 3x − y=15......(2)
Add equation (1) and equation (2),
⇒ 4x = 40
⇒ x = 10
Substitute x = 10 in equation (1),
⇒ y = 25 − 10 = 15
Therefore, the cost of one pen and one pencil box are ₹10 and ₹15, respectively.
Q.5. Determine, algebraically, the vertices of the triangle formed by the lines
3x – y = 3
2x – 3y = 2
x + 2y = 8
The common solution of the two equations forming its two sides is the vertex of the triangle.
Consider, the two lines AB: 3x − y = 3, BC: 2x − 3y = 2
Multiply 3x − y = 3 by 3 and subtract 2x − 3y = 2 from it.
⇒ (9x − 3y)−(2x−3y) = 9 − 2
⇒ 7x = 7
⇒ x = 1
Put x in 3x − y = 3
⇒ 3 × 1 − y = 3
⇒ y = 0
Thus, vertex B is (1, 0).
Now, consider the two lines AC: x + 2y = 8 and BC: 2x − 3y = 2Multiply x + 2y = 8 by 2 and subtract 2x − 3y = 2 from it.
⇒ (2x + 4y)−(2x − 3y) = 16 − 2
⇒ 7y = 14
⇒ y =2
Put y in x + 2y = 8
⇒ x + 2 × 2 = 8
⇒ x = 8 − 4
⇒ x = 4
Thus, vertex C is (4, 2).
Now, consider the lines AB: 3x − y = 3 and AC: x + 2y = 8Multiply 3x − y = 3 by 2 and add x + 2y = 8
⇒ (6x − 2y) + (x + 2y) = 6 + 8
⇒ 7x = 14
⇒ x = 2
Put x in 3x − y = 3
⇒ 3×2 − y = 3
⇒ y = 6 − 3
⇒ y = 3
Thus, vertex A is (2, 3).
Therefore, the vertices of the △ABC are A(2, 3),B(1, 0) and C(4, 2)
Q.6. Ankita travels 14 km to her home partly by rickshaw and partly by bus. She takes half an hour if she travels 2 km by rickshaw, and the remaining distance by bus. On the other hand, if she travels 4km by rickshaw and the remaining distance by bus, she takes 9 minutes longer. Find the speed of the rickshaw and of the bus.
Let the speed of the rickshaw and the bus are x and y km/h, respectively.
Now, she has taken time to travel 2 km by rickshaw, t1 = (2/x) hr
Speed = distance/ time
she has taken time to travel remaining distance i.e., (14 – 2) = 12km
By bus t2 = (12/y) hr
By first condition,
t1 + t2 = ½ = (2/x) + (12/y) … (i)
Now, she has taken time to travel 4 km by rickshaw, t3 = (4/x) hr
and she has taken time to travel remaining distance i.e., (14 – 4) = 10km, by bus = t4 = (10/y) hr
By second condition,
t3 + t4 = ½ + 9/60 = ½ + 3/20
(4/x) + (10/y) = (13/20) …(ii)
Let (1/x) = u and (1/y) = v
Then Equations. (i) and (ii) becomes
2u + 12v = ½ …(iii)
4u + 10v = 13/20…(iv)
[First, multiply Eq. (iii) by 2 and then subtract]
(4u + 24v) – (4u + 10v) = 1–13/20
14v = 7/20
v = 1/40
Substituting the value of v in Eq. (iii),
2u + 12(1/40) = ½
2u = 2/10
u = 1/10
x = 1/u = 10km/hr
y = 1/v = 40km/hr
Hence, the speed of rickshaw = 10 km/h
And the speed of bus = 40 km/h.
Q.7. A person, rowing at the rate of 5 km/h in still water, takes thrice as much time in going 40 km upstream as in going 40 km downstream. Find the speed of the stream.
Consider,
Speed of rowing by a person = 5 km/hr.
Speed of stream = x km/hr
Upstream Speed = (5−x) km/hr
Downstream speed = (5+x) km/hr
According to the question,⇒ 5 + x = 15 − 3x
⇒ 4x = 10
⇒ x = 2.5 km/hr
Q.8. A motor boat can travel 30 km upstream and 28 km downstream in 7 hours. It can travel 21 km upstream and return in 5 hours. Find the speed of the boat in still water and the speed of the stream.
Let the speed of the boat in still water be x km/h and speed of the stream is y km/h.
Therefore, speed of the boat while upstream is (x − y) km/h and speed of the boat while downstream is (x + y) km/h
As we know that speed= (distance/time), therefore, time = (distance/speed)
It is given that the motor boat can travel 30 km upstream and 28 km downstream in 7 hours and also it can travel 21 km upstream and return in 5 hours, thus,...(1)
...(2)
Let
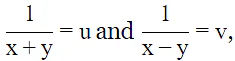
then the equations (1) and (2) becomes:
30u + 28v = 7 ...(3)
21u + 21v = 5 ...(4)
Multiplying equation (3) by 21 and equation (4) by 30 we get,
630u + 588v = 147 ...(5)
630u + 630v = 150 ...(6)
Now subtracting equation (5) from equation (6), we get
42v = 3
⇒ v = (1/14)
Substitute the value of v in equation (4) then, u = (1/6)
Since (1/(x+y)) = u and (1/(x+y)) = v, therefore,
x + y = 6 ...(7)
x − y = 14 ...(8)
Adding equations (7) and (8), we get:
2x = 20
⇒ x = 10
Hence, the speed of the boat in still water is 10 km/h. and speed of the stream is 4 km/h.
Q.9. A two-digit number is obtained by either multiplying the sum of the digits by 8 and then subtracting 5 or by multiplying the difference of the digits by 16 and then adding 3. Find the number.
Let the two-digit number be 10x + y.
Case I: Multiplying the sum of digits by 8 and then subtracting 5 two-digit number
⇒ 8(x + y) − 5 = 10x + y
⇒ 8x + 8y − 5=10x + y
⇒ 2x − 7y = −5… (i)Case II: Multiplying the difference of digits by 16 and then adding 3 two-digit number
⇒ 16(x − y) + 3 = 10x + y
⇒ 16x−16y + 3 = 10x + y
⇒ 6x − 17y = −3… (ii)Multiply (i) by 3 and subtract from (ii):
⇒(6x − 17y)−(6x − 21y) = −3 − (−15)
⇒ 4y = 12
⇒ y = 3
Put y in equation (i):
⇒ 2x − 7 × 3 = −5
⇒ 2x = 21 − 5 = 16
⇒ x = 8
Therefore, the required two-digit number =10x + y = 10 × 8 + 3 = 80 + 3 = 83
Q.10. A railway half ticket costs half the full fare, but the reservation charges are the same on a half ticket as on a full ticket. One reserved first class ticket from the station A to B costs Rs 2530. Also, one reserved first class ticket and one reserved first class half ticket from A to B costs Rs 3810. Find the full first class fare from station A to B, and also the reservation charges for a ticket.
Assume the required unknown to be equal to some variables
Let the reservation charges be Rs. x and cost of full ticket of first class be Rs. y
It is given that one reserved first class ticket from the station A to B costs Rs. 2530. Also, one reserved first class ticket and one reserved first class half ticket from A to B costs Rs. 3810, therefore, x + y = 2530 ...(1) and since railway half ticket costs half the full fare, but the reservation charges are the same on a half ticket as on a full ticket. So, we get,Multiply (1) by 4 and subtract from (2)
Hence, the full first class fare from station A to B is Rs. 2500 and the reservation charge for the ticket is ₹30.
Q.11. A shopkeeper sells a saree at 8% profit and a sweater at 10% discount, thereby, getting a sum Rs 1008. If she had sold the saree at 10% profit and the sweater at 8% discount, she would have got Rs 1028. Find the cost price of the saree and the list price (price before discount) of the sweater.
Let the cost price of the saree and the first of the sweater be Rs. x and Rs. y, respectively case I sell a saree at 8% profit + sells a sweater at 10% discount = Rs 1008
⇒ (100 + 8)% of x + (100 – 10)% of y 1008
⇒ 108% of x + 90% of y = 1008
⇒ 1.08x + 0.9y = 1008
Case II Sold the saree at 10% profit + Sold the sweater at 8% discount = Rs. 1028
⇒ (100 + 10)% of x + (100 – 8)% of y = 1028
⇒ 110% of x + 92% of y = 1028
⇒ 1.1x + 0.92y = 1028
On putting the value of y from Eq. (i) into Eq. (ii), we get
1.1x + 0.92((1008-108x)/0.9) = 1028
⇒ 1.1 × 0.9x + 927.36 – 0.9936x = 1028 × 0.9 × 0.99x – 0.9936x = 9252 – 927.36
⇒ 0.0036x = 2.16
⇒ x = (2.16)/0.0036 = 600
On putting the value of x in Eq. (i), we get
1.08 × 600 + 0.9y = 1008
⇒ 108 × 6 + 0.9y = 1008
⇒ 0.9y = 1008 – 648
⇒ 0.9y = 360
⇒ y = (360/0.9) = 400
Hence, the cost price of the saree and the list price (price before discount) of the sweater are Rs. 600 and Rs. 400, respectively.
Q.12. Susan invested certain amount of money in two schemes A and B, which offer interest at the rate of 8% per annum and 9% per annum, respectively. She received Rs 1860 as annual interest. However, had she interchanged the amount of investments in the two schemes, she would have received Rs 20 more as annual interest. How much money did she invest in each scheme?
Let amount invested in A be Rs. x and in B be Rs. y.
As per the given statements, 0.08x + 0.09y = 1860.....(1)
And, 0.09x + 0.08y = 1880.....(2)
Multiplying equation (1) with 8 we get, 0.64x + 0.72y = 14880 ...(3)
Multiplying equation (2) with 9 we get, 0.81x + 0.72y = 16920 ...(4)
Subtracting equation (3) from (4), we get 0.17x = 2040 ⇒ x = 12000
Substituting x = 12000 in the equation (1), we get 0.08(12000) + 0.09y = 1860 ⇒ y = 10000
Hence, amount invested A is Rs. 12000 and in B is Rs. 10000
Q.13. Vijay had some bananas, and he divided them into two lots A and B. He sold the first lot at the rate of Rs 2 for 3 bananas and the second lot at the rate of Re 1 per banana, and got a total of Rs 400. If he had sold the first lot at the rate of Re 1 per banana, and the second lot at the rate of Rs 4 for 5 bananas, his total collection would have been Rs 460. Find the total number of bananas he had.
Let the number of bananas in lots A and B be x and y respectively
Case I: Cost of first lot at the rate of ₹2 for 3 bananas + Cost of second lot at the rate of ₹1 per banana =₹400
Case II: Cost of first lot at the rate ₹ 1 per banana + Cost of second lot at the rate of ₹ 4 for 5 bananas = amount received
Multiply (1) by 4 and (2) by 3 and subtract them.
Put x in equation (1),
The total number of bananas = Number of bananas in lot A+ Number of bananas in lot B = x + y = 300 + 200 = 500
Therefore, he had 500 bananas.
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Exemplar: Pair of Linear Equations in Two Variables- 2 - Mathematics (Maths) Class 10
| 1. What is the importance of understanding pair of linear equations in two variables? |  |
| 2. How can we determine the number of solutions for a pair of linear equations in two variables? |  |
| 3. How do we solve a pair of linear equations in two variables using the substitution method? |  |
| 4. Can a pair of linear equations in two variables have no solution? |  |
| 5. How do we graphically represent a pair of linear equations in two variables? |  |