NCERT Exemplar Solutions: Linear Equations in Two Variables | Mathematics (Maths) Class 9 PDF Download
| Table of contents |

|
| Exercise 4.1 |

|
| Exercise 4.2 |

|
| Exercise 4.3 |

|
| Exercise 4.4 |

|
Exercise 4.1
Write the correct answer in each of the following:
Q.1. The linear equation 2x – 5y = 7 has
(a) A unique solution
(b) Two solutions
(c) Infinitely many solutions
(d) No solution
Correct Answer is Option (c)
Expressing y in terms of x in the equation 2x – 5y = 7, we get,
2x – 5y = 7
– 5y = 7 – 2x
y = (7 – 2x)/– 5
Hence, we can conclude that the value of y will be different for different values of x.
Hence, option c is the correct answer.
Q.2. The equation 2x + 5y = 7 has a unique solution, if x, y are:
(a) Natural numbers
(b) Positive real numbers
(c) Real numbers
(d) Rational numbers
Correct Answer is Option (a)
Consider, 2x + 5y = 7
x
1
y
1
(a) (1, 1) is a solution of 2x + 5y = 7
(b) If positive real numbers are chosen, 2x + 5y = 7 will have many solutions.
(c) If real numbers are chosen, 2x + 5y = 7 will have infinite solutions.
(d) If rational numbers are chosen, 2x + 5y = 7 will have many solutions.
Hence, option a is the correct answer.
Q.3. If (2, 0) is a solution of the linear equation 2x + 3y = k, then the value of k is
(a) 4
(b) 6
(c) 5
(d) 2
Correct Answer is Option (a)
We know that,
(2, 0) = (x, y)
Substituting values of x and y in the above equation, we get
2 × 2 + 3 × 0 = k
k = 4
Hence, option a is the correct answer.
Q.4. Any solution of the linear equation 2x + 0y + 9 = 0 in two variables is of the form
(a) (-9/2, m)
(b) (n, -9/2)
(c) (0, -9/2)
(d) (– 9, 0)
Correct Answer is Option (a)
Solving the above equation we get,
2x = -9
x = -9/2
As the coefficient of y is 0, therefore, y can take any value and will not affect our answer.
(a) x = -9/2
y = any value
(b) x = n
(c) x = 0
(d) x = -9
Hence, option a is the correct answer.
Q.5. The graph of the linear equation 2x + 3y = 6 cuts the y – axis at the point
(a) (2, 0)
(b) (0, 3)
(c) (3, 0)
(d) (0, 2)
Correct Answer is Option (d)
Let 2x + 3y = 6 cut the y-axis at P. therefore at P x-coordinate = 0.
Substituting x = 0, we get
2(0) + 3y = 6
3y = 6
y = 2
Hence the coordinates are (0, 2).
a. (2, 0) is wrong because it has x = 2
b. (0, 3) is wrong because it has y = 3
c. (3, 0) is wrong because it has x = 3
d. (0, 2) is right because it has x = 0 and y = 2 which is equal to the coordinates (0,2)
Hence, option d is the correct answer.
Q.6. The equation x = 7, in two variables, can be written as
(a) 1. x + 1. y = 7
(b) 1. x + 0. y = 7
(c) 0. x + 1. y = 7
(d) 0. x + 0. y = 7
Correct Answer is Option (b)
(a) Simplifying the equation we get x + y = 7
(b) Simplifying the equation we get x + 0y = 7 which is equal to x = 7
(c) Simplifying the equation we get y = 7
(d) simplifying the equation we get 0x + 0y = 7 which is not possible.
Hence, option (b) is the correct answer.
Q.7. Any point on the x – axis is of the form
(a) (x, y)
(b) (0, y)
(c) (x, 0)
(d) (x, x)
Correct Answer is Option (c)
Any point on the x-axis has its ordinate 0.
So, any point on the x-axis if of the form (x, 0).
Hence, option (C) is the correct answer.
Q.8. Any point on the line y = x is of the form
(a) (a, a)
(b) (0, a)
(c) (a, 0)
(d) (a, – a)
Correct Answer is Option (a)
Any point on the line y = x will have x and y coordinate same.
So, any point on the line y = x is of the form (a, a).
Hence, option (a) is the correct answer.
Q.9. The equation of x – axis is of the form
(a) x = 0
(b) y = 0
(c) x + y = 0
(d) x = y
Correct Answer is Option (b)
The equation of x-axis is y = 0, since, x-axis is a parallel to itself at a distance 0 from it.
Hence, option (b) is the correct answer.
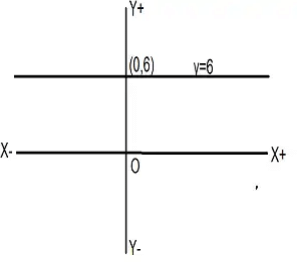
Q.10. The graph of y = 6 is a line
(a) parallel to x-axis at a distance 6 units from the origin
(b) parallel to y-axis at a distance 6 units from the origin
(c) making an intercept 6 on the x-axis.
(d) making an intercept 6 on both the axes.
Correct Answer is Option (a)
The given equation is y=6
We can write it as y=0.x+6
i.e. for every value of x, we have y=6
So, the points are (0,6),(−1,6),(1,6),(3,6)....
On plotting these points, we get a straight line parallel to the x−axis at a distance of 6 units from the x−axis.
Q.11. x = 5, y = 2 is a solution of the linear equation
(a) x + 2 y = 7
(b) 5x + 2y = 7
(c) x + y = 7
(d) 5 x + y = 7
Correct Answer is Option (c)
Given
x = 5, y = 2
x + y = 5 + 2(2) = 9
5x + 2y = 5(5) + 2(2) = 29
x + y = 7
5x + y = 5(5) + 2 = 27
x = 5, y = 2 is solution of x + y = 7
Q.12. If a linear equation has solutions (–2, 2), (0, 0) and (2, – 2), then it is of the form
(a) y – x = 0
(b) x + y = 0
(c) –2x + y = 0
(d) –x + 2 y = 0
Correct Answer is Option (b)
Given the points A(−2, 2), B(0, 0), C((2, 2) are solutions of a linear equations.
Let line equation ⇒ y = mx + c
Since (0, 0) lies on it, c = 0
Since (−2, 2) lies on it, 2 = −(2)(m) ⇒ m=−1
So, y = −x
⇒ x + y = 0 is the equation of line.
Q.13. The positive solutions of the equation ax + by + c = 0 always lie in the
(a) 1st quadrant
(b) 2nd quadrant
(c) 3rd quadrant
(d) 4th quadrant
Correct Answer is Option (a)
Let the positive solutions be of the form (p,q)
Since, the abscissa p is positive, so it will lie towards the positive direction of X-axis
Again, the ordinate q is positive. So, it will lie towards the positive direction of Y-axis
∴(p, q) will lie in the Ist quadrant.
Q.14. The graph of the linear equation 2x + 3y = 6 is a line which meets the x-axis at the point
(a) (0, 2)
(b) (2, 0)
(c) (3, 0)
(d) (0, 3)
Correct Answer is Option (c)
2x + 3y = 6 will meet the x−axis at y = 0.
For y = 0, x = 3.
∴ The point is (3, 0)
Q.15. The graph of the linear equation y = x passes through the point
(a) ((3/2), ((-3)/2)
(b) 0, (3/2)
(c) (1, 1)
(d) ((-1)/2, (1/2))
Correct Answer is Option (c)
As y = x is a linear equation , means the value of y is same as value of x.
Thus checking in options :
when x = 1, then y = 1 is the only option where the value of y = x.
Hence option c is correct.
Q.16. If we multiply or divide both sides of a linear equation with a non-zero number, then the solution of the linear equation :
(a) Changes
(b) Remains the same
(c) Changes in case of multiplication only
(d) Changes in case of division only
Correct Answer is Option (b)
As we know, if we multiply or divide both sides of a linear equation with a non-zero number, then the solution of the linear equation remains unchanged.
Thus, we can say that the solution remains the same.
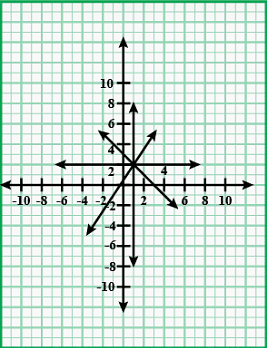
Q.17. How many linear equations in x and y can be satisfied by x = 1 and y = 2?
(a) Only one
(b) Two
(c) Infinitely many
(d) Three
Correct Answer is Option (c)
From the graph, its clear that infinite straight lines can pass through the point (1, 2).
So, infinite linear equation are possible satisfying x = 1, y = 2
Q.18. The point of the form (a, a) always lies on :
(a) x-axis
(b) y-axis
(c) On the line y = x
(d) On the line x + y = 0
Correct Answer is Option (c)
The point having same abscissa and same ordinates lies on the same line y = x
Hence point (a, a) lies on y = x
Q.19. The point of the form (a, – a) always lies on the line
(a) x = a
(b) y = – a
(c) y = x
(d) x + y = 0
Correct Answer is Option (d)
For the point of the form (a,−a) to lie on the line, its co ordinates should satisfy the equation,
(a) For the line x=a,
There is no y-coordinate, so it is 0
Since the point (a,−a) have y=−a, it does not lie on the line.
(b) For the line y=a,
There is no x-value, so x coordinate is 0
Since the point (a,−a) haveit does not lie on the line.
(c) For the line y=x,Both x and y co ordinates should be equal
Since, co ordinates of the point (a,−a) are not equal, it does not lie on the line.
(d) For the line x+y=0
Sum of x and y coordinates should be 0
Substituting co ordinates of the point (a,−a) in the equation x+y=0
We get a+(−a)=a−a=0
LHS = RHS
Hence, (a,−a) satisfies x + y = 0.
Hence, option d is correct.
Exercise 4.2
Write whether the following statements are True or False? Justify your answers:
Q.1. The point (0, 3) lies on the graph of the linear equation 3x + 4y = 12.
True.
We have the equation, 3x + 4y = 12.
Substituting the values of x = 0 and y = 3 from the point (0, 3) in the equation,
We get,
3(0) + 4(3) = 12 = RHS.
Hence, the point (0, 3) lies on the graph of the linear equation 3x + 4y = 12.
Q.2. The graph of the linear equation x + 2y = 7 passes through the point (0, 7).
False.
We have the equation, x + 2y = 7.
Substituting the values of x = 0 and y = 7 from the point (0, 7) in the equation,
We get,
0 + 2(7) = 14 ≠RHS
Hence, the graph of the linear equation x + 2y = 7 passes through the point (0, 7).
Q.3. The graph given below represents the linear equation x + y = 0.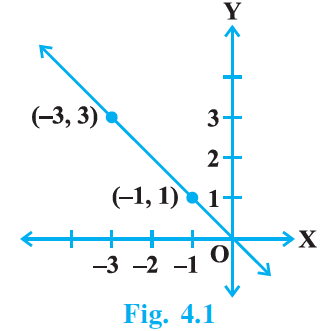
True.
We have the equation, x + y = 0.
x + y = 0
x = – y
from the graph, we get the points (– 3, 3) and (– 1, 1),
Considering the point (– 3, 3)
x = – 3 and y = 3
Hence, substituting (– 3, 3) in equation,
We get,
– 3 = 3 which satisfies the equation x = – y
Considering the point – 1, 1)
x = – 1 and y = 1
Hence, substituting (– 1, 1) in equation,
We get,
– 1 = 1 which satisfies the equation x = – y
Therefore, the given solution: (– 3, 3) and (– 1, 1) satisfies the given equation x = – y.
Hence, the given graph represents the linear equation x + y = 0.
Q.4. The graph given below represents the linear equation x = 3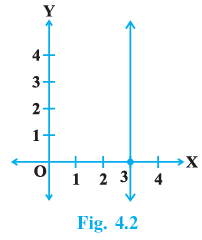
True
From the graph, it is clear that the given line is parallel to the y-axis and at a distance of 3 units from the y-axis.
Also, each point on the line is of the form (3,a) i.e. x = 3, and y can have any real value.
So, the equation of line is x = 3.
Q.5. The coordinates of points in the table:
represent some of the solutions of the equation x – y + 2 = 0.
False
The points (0, 2),(1, 3),(2, 4) and (4, 6) satisfy the given equation x − y + 2 = 0.
Each of these points is the solution of the equation x−y+2−0.
But, in the equation if we put (3, −5) i.e 3−(−5) + 2 = 0, i.e., 3 + 5 = 0 orit does not satisfy the equation, So, it is false.hence, the given statement false, since the point (3,−5) does not satisfy the given equation
Q.6. Every point on the graph of a linear equation in two variables does not represent a solution of the linear equation.
False
A graph of linear equation in two variables is constructed by joining the points which are the solutions of the given equation.
So, any point on the graph must be a solution of the linear equation.
Therefore, the given statement is false.
Q.7. The graph of every linear equation in two variables need not be a line.
False
Every linear equation in two variables can be written as y=mx+c.
Here, for each value of x there is a unique value of y.
Also, x & y are in direct variation.
Hence, (y/x) will always remain constant.Consequently, the graph will maintain a definite slope making it a straight line.
∴ The given statement is false.
Exercise 4.3
Q.1. Draw the graphs of linear equations y = x and y = – x on the same Cartesian plane. What do you observe?
According to the question,
y = x ...eq (i)
Values of x and y satisfying the equation =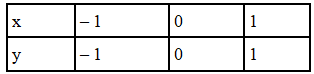
y = -x ...(ii)
Values of x and y satisfying the equation=
Plotting the graph: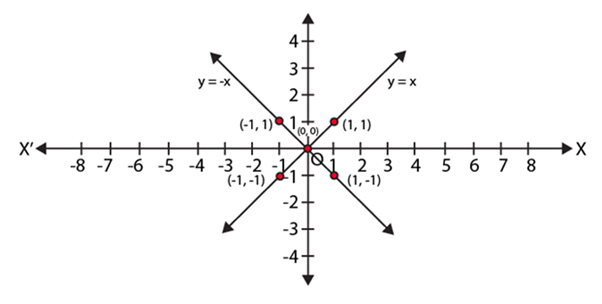
From the above graph,
We observe that the two lines y = x and y = – x intersect each other at O (0, 0).
Q.2. Determine the point on the graph of the linear equation 2x + 5y = 19 whose ordinate is 1½ times its abscissa.
From the question, we have,
2x + 5y = 19 …(i)
According to the question,
Ordinate is 1½ times its abscissa
⇒ y = 1½ x = (3/2) x
Substituting y = (3/2)x in eq. (i)
We get,
2x + 5 (3/2) x = 19
(19/2)x = 19
x = 2
Substituting x = 2 in eq. (i)
We get
2x + 5y = 19
2(2) + 5y = 19
y = (19 – 4)/5 = 3
Hence, we get x =2 and y = 3
Thus, point (2, 3) is the required solution.
Q.3. Draw the graph of the equation represented by a straight line which is parallel to the x-axis and at 3 units below.
According to the question,
We get the linear equation,
y = – 3
Values of x and y satisfying the equation =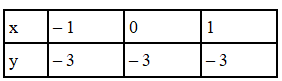
Plotting the graph: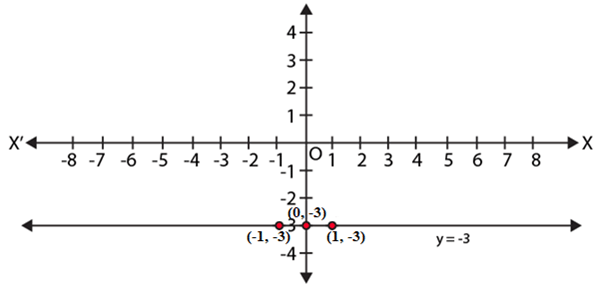
Q.4. Draw the graph of the linear equation whose solutions are represented by the points having the sum of the coordinates as 10 units.
According to the question,
We get the linear equation,
x + y = 10
We get,
x = 10 – y
Values of x and y satisfying the equation =

Plotting the graph: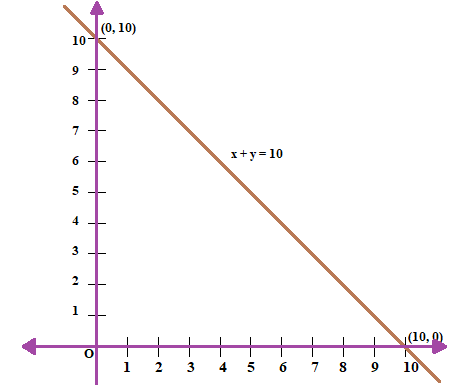
Q.5. Write the linear equation such that each point on its graph has an ordinate 3 times its abscissa.
According to the question,
A linear equation such that each point on its graph has an ordinate(y) which is 3 times its abscissa(x).
So we get,
⇒ y = 3x.
Hence, y = 3x is the required linear equation.
Q.6. If the point (3, 4) lies on the graph of 3y = ax + 7, then find the value of a.
If (3, 4) lies in the equation 3y = ax + 7, then the must satisfy the equation of the line.
Thus, 3(4) = a(3)+7
⇒ 12 = 3a+7
⇒ a = (5/3)
Q.7. How many solution(s) of the equation 2x + 1 = x – 3 are there on the :
(i) Number line
(ii) Cartesian plane
(i) The number of solutions (s) of the equation 2x − 1 = x − 3 which are on the number line is one.
2x − 1 = x − 3 ⇒ 2x − x = −3 − 1 ⇒ x = −4
∴ x = −4 is the solution of the given equation
(ii) As in the Cartesian Plane the equation can be written as x + 0y = −4. And for infinitely many values of y we have infinite values of x. So The number of solution (s) of the equation 2x + 1 = x − 3 which are on the Cartesian plane are infinitely many solutions.
Q.8. Find the solution of the linear equation x + 2y = 8 which represents a point on
(i) x-axis
(ii) y-axis
(i) We know that the point which lies on x-axis has its ordinate 0.
So, putting y=0 we get:
x + 2 × 0 = 8 ⇒ x = 8
hence, (8, 0) lies on the x-axis
(ii) We know that the point which lies on y-axis has its abscissa 0.
So, putting x = 0 we get:
0 + 2y = 8 ⇒ 2y = 8 ⇒ y = 4
hence, (0, 4) lies on the y-axis
Q.9. For what value of c, the linear equation 2x + cy = 8 has equal values of x and y for its solution.
2x - cy = 8 and x =y
so, 2x - cx = 8
x (2 - c) = 8
x = 8 / (2-c)
denominator should not be zero
so, 2 - c = 0
c = 2
Except for the value of c=2, a solution can be found.
Q.10. Let y varies directly as x. If y = 12 when x = 4, then write a linear equation. What is the value of y when x = 5?
y varies of directly as x. This means that the equation is of the form y=kx where k is any number.
Substituting y = 12 when x = 4, we get
12 = k × 4 ⇒ k = 3
Hence, the required equation is y = 3x.
The value of y when x = 5 is y = 3x5 = 15.
 |
Download the notes
NCERT Exemplar Solutions: Linear Equations in Two Variables
|
Download as PDF |
Exercise 4.4
Q.1. Show that the points A (1, 2), B ( – 1, – 16) and C (0, – 7) lie on the graph of the linear equation y = 9x – 7.
We have the equation,
y = 9x – 7
For A (1, 2),
Substituting the values of (x, y) = (1, 2),
We get,
2 = 9(1) – 7 = 9 – 7 = 2
For B (–1, –16),
Substituting the values of (x,y) = (–1, –16),
We get,
–16 = 9(–1) – 7 = – 9 – 7 = – 16
For C (0, –7),
Substituting the values of (x, y) = (0, –7),
We get,
– 7 = 9(0) – 7 = 0 – 7 = – 7
Hence, we find that the points A (1, 2), B (–1, –16) and C (0, –7) satisfies the line y = 9x – 7.
Hence, A (1, 2), B (–1, –16) and C (0, –7) are solutions of the linear equation y = 9x – 7
Therefore, points A (1, 2), B (–1, –16), C (0, –7) lie on the graph of linear equation y = 9x – 7.
Q.2. The following observed value of x and y are thought to satisfy a linear equation. Write the linear equation-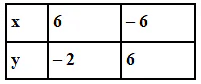
Draw the graph using the value of x, y as given in the above table. At what points the graph of the linear equation (i) cuts the X-axis ? (ii) cuts the Y-axis?
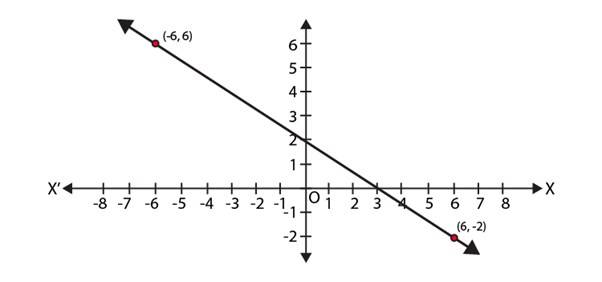 We know that,
We know that,
The linear equation of a line is,
y = mx + c, where, c is the y-intercept
From the graph,
We get y-intercept is 2.
⇒ c = 2.
Also, from the graph,
We get,
x1 = 6, y1 = – 2 and x2 = – 6, y2 = 6
We know that,
m = slope of the line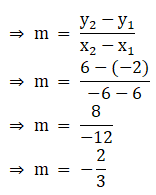
∴ we get the linear equation,
y = – (2/3)x + 2
Multiplying whole equation by 3, we get,
⇒ 3y = – 2x + 6
⇒ 2x + 3y – 6 = 0
Thus, the points the graph of the linear equation cuts
(i) x-axis
Since, the point is on x axis, we have, y = 0.
Substituting y = 0 in the equation, 2x + 3y – 6 = 0,
We get,
2x + 3 × 0 – 6 = 0
⇒ 2x = 6
⇒ x = 3
Hence, the point at which the graph cuts x-axis = (3, 0).
(ii) y-axis
Since, the point is on y axis, we have, x = 0.
Substituting x = 0 in the equation, 2x + 3y – 6 = 0,
We get,
2 × 0 + 3y – 6 = 0
⇒ 3y = 6
⇒ y = 2
Hence, the point at which the graph cuts x-axis = (0, 2).
Q.3. Draw the graph of the linear equation 3x + 4y = 6. At what points, the graph cuts X and Y-axis?
According to the question,
We get the equation,
3x + 4y = 6.
We need at least 2 points on the graph to draw the graph of this equation,
Thus, the points the graph cuts
(i) x-axis
Since, the point is on x axis, we have, y = 0.
Substituting y = 0 in the equation, 3x + 4y = 6,
We get,
3x + 4×0 = 6
⇒ 3x = 6
⇒ x = 2
Hence, the point at which the graph cuts x-axis = (2, 0).
(ii) y-axis
Since, the point is on y axis, we have, x = 0.
Substituting x = 0 in the equation, 3x + 4y = 6,
We get,
3 ×0 + 4y = 6
⇒ 4y = 6
⇒ y = 6/4
⇒ y = 3/2
⇒ y = 1.5
Hence, the point at which the graph cuts x-axis = (0, 1.5).
Plotting the points (0, 1.5) and (2, 0) on the graph.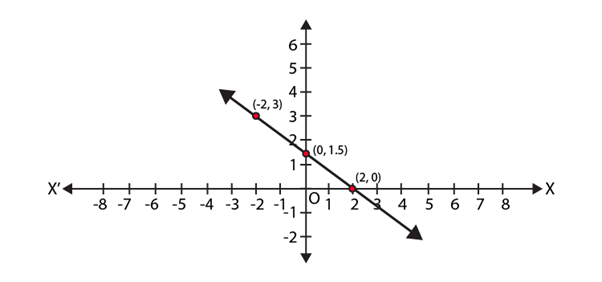
Q.4. The linear equation that converts Fahrenheit (F) to Celsius (C) is given by the relation 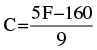
(i) If the temperature is 86°F, what is the temperature in Celsius?
(ii) If the temperature is 35°C, what is the temperature in Fahrenheit?
(iii) If the temperature is 0°C what is the temperature in Fahrenheit and if the temperature is 0°F, what is the temperature in Celsius?
(iv) What is the numerical value of the temperature which is same in both the scales?
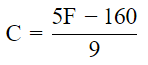
(i) Putting F = 86°, we get C = 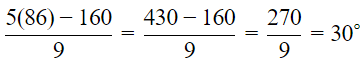
Hence, the temperature in Celsius in 30° C.
(ii) Putting C = 35°, we get 35° = 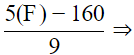 315° = 5F − 160
315° = 5F − 160
⇒ 5F = 315 + 160 = 475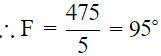
Hence, the temperature in Fahrenheit is 95° F.
(iii) Putting C = 0°, we get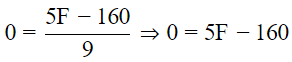
⇒ 5F = 160
∴ F = (160/5) = 32°
Now, putting F = 0∘, we get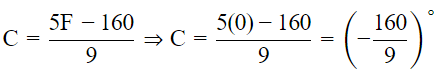
If the temperature is 0° C, the temperature in Fahrenheit is 32° and if the temperature is 0° F, then the temperature in Celsius is 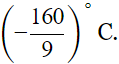
(iv) Putting C = F, in the given relation, we get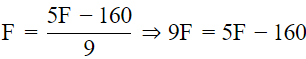
⇒ 4F = −160
∴ F = (-160)/4 = 40∘
Hence, the numerical value of the temperature which is same in both the sacales is −40.
Q.5. If the temperature of a liquid can be measured in Kelvin units as x°K or in Fahrenheit units as y°F, the relation between the two systems of measurement of temperature is given by the linear equation y = (9/5) (x – 273) + 32
(i) Find the temperature of the liquid in Fahrenheit if the temperature of the liquid is 313°K.
(ii) If the temperature is 158° F, then find the temperature in Kelvin.
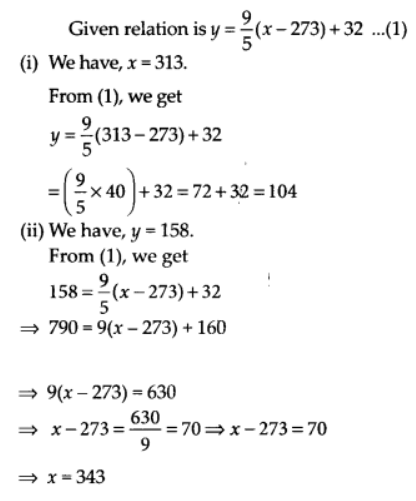
Q.6. The force exerted to pull a cart is directly proportional to the acceleration produced in the body. Express the statement as a linear equation of two variables and draw the graph of the same by taking the constant mass equal to 6 kg. Read from the graph, the force required when the acceleration produced is (i) 5 m/sec 2, (ii) 6 m/sec2.
We have y x
Where y denotes the force, x denotes the acceleration and m denotes the constant mass.
Taking m = 6kg, we get y = 6x
Now, we form a table as following the value of y below the corresponding value of x.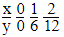
Plot the points (0, 0),(1, 6) and (2, 12) on a graph paper and join any two points and obtain a line.
From the graph we see that if the acceleration is 5m/sec2 the force is 30 N and if the accleration is 6m/see2 , then the force is 36 N.
|
40 videos|420 docs|51 tests
|
FAQs on NCERT Exemplar Solutions: Linear Equations in Two Variables - Mathematics (Maths) Class 9
| 1. What are linear equations in two variables? |  |
| 2. How can we solve linear equations in two variables? |  |
| 3. What is the significance of the solution of a linear equation in two variables? |  |
| 4. Can a linear equation in two variables have more than one solution? |  |
| 5. What are some real-life applications of linear equations in two variables? |  |
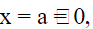 it does not lie on the line.
it does not lie on the line.
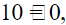 it does not satisfy the equation, So, it is false.hence, the given statement false, since the point (3,−5) does not satisfy the given equation
it does not satisfy the equation, So, it is false.hence, the given statement false, since the point (3,−5) does not satisfy the given equation































