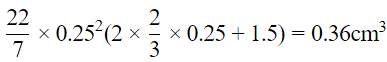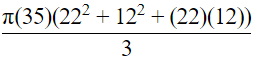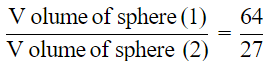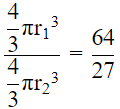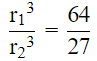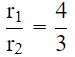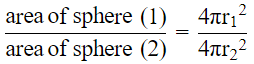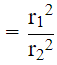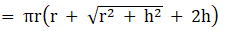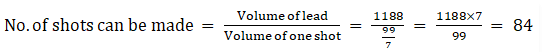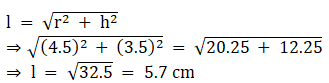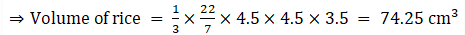NCERT Exemplar: Surface Areas & Volumes | Mathematics (Maths) Class 10 PDF Download
| Table of contents |

|
| Exercise 12.1 |

|
| Exercise 12.2 |

|
| Exercise 12.3 |

|
| Exercise 12.4 |

|
Exercise 12.1
Choose the correct answer from the given four options:
Q.1. A cylindrical pencil sharpened at one edge is the combination of
(a) a cone and a cylinder
(b) frustum of a cone and a cylinder
(c) a hemisphere and a cylinder
(d) two cylinders.
Correct Answer is Option (a)
The Nib of a sharpened pencil = conical shape
The rest of the part of a sharpened pencil = cylindrical
Therefore, a pencil is a combination of cylinder and a cone.
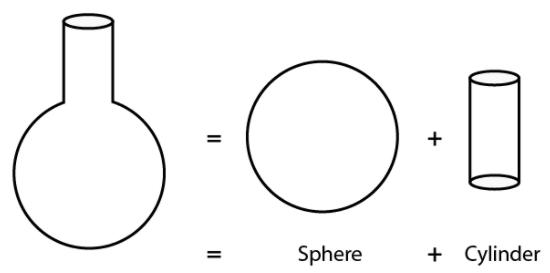
Q.2. A surahi is the combination of
(a) a sphere and a cylinder
(b) a hemisphere and a cylinder
(c) two hemispheres
(d) a cylinder and a cone.
Correct Answer is Option (a)
The top part of surahi = cylindrical shape
Bottom part of surahi = spherical shape
Therefore, surahi is a combination of Sphere and a cylinder.
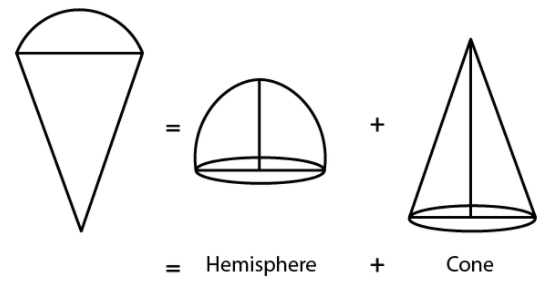
Q.3. A plumbline (sahul) is the combination of (see Figure)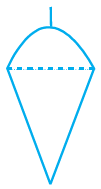 (a) a cone and a cylinder
(a) a cone and a cylinder
(b) a hemisphere and a cone
(c) frustum of a cone and a cylinder
(d) sphere and cylinder
Correct Answer is Option (b)
The upper part of plumbline = hemispherical,
The bottom part of plumbline = conical
Therefore, it is a combination of hemisphere and cone.
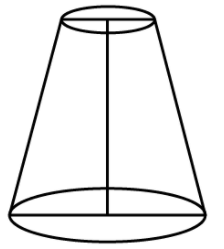
Q.4. The shape of a glass (tumbler) (see Figure) is usually in the form of
(a) a cone
(b) frustum of a cone
(c) a cylinder
(d) a sphere
Correct Answer is Option (b)
The shape of glass is a frustum or specifically, an inverted frustum.
Q.5. The shape of a gilli, in the gilli-danda game (see Figure), is a combination of
 (a) two cylinders
(a) two cylinders
(b) a cone and a cylinder
(c) two cones and a cylinder
(d) two cylinders and a cone
Correct Answer is Option (c)
The left and right part of a gilli = conical
The central part of a gilli = cylindrical
Therefore, it is a combination of a cylinder and two cones.
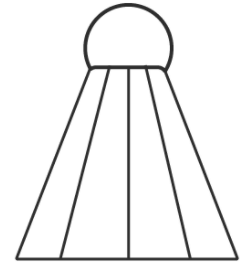
Q.6. A shuttle cock used for playing badminton has the shape of the combination of
(a) a cylinder and a sphere
(b) a cylinder and a hemisphere
(c) a sphere and a cone
(d) frustum of a cone and a hemisphere
Correct Answer is Option (d)
The cork of a shuttle = hemispherical shapes
The upper part of a shuttle = shape of frustum of a cone.
Therefore, it is a combination of frustum of a cone and a hemisphere.
Q.7. A cone is cut through a plane parallel to its base and then the cone that is formed on one side of that plane is removed. The new part that is left over on the other side of the plane is called
(a) a frustum of a cone
(b) cone
(c) cylinder
(d) sphere
Correct Answer is Option (a)
When a cone is divided into two parts by a plane through any point on its axis parallel to its base, the upper and lower parts obtained are cone and a frustum respectively.
Q.8. A hollow cube of internal edge 22cm is filled with spherical marbles of diameter 0.5 cm and it is assumed that 1/8 space of the cube remains unfilled. Then the number of marbles that the cube can accommodate is
(a) 142296
(b) 142396
(c) 142496
(d) 142596
Correct Answer is Option (a)
According to the question,
Volume of cube =223=10648cm3
Volume of cube that remains unfilled =1/8×10648=1331cm3
Volume occupied by spherical marbles =10648−1331=9317cm3
Radius of the spherical marble = 0.5/2=0.25cm=1/4cm
Volume of 1 spherical marble = 4/3×22/7 × (1/4)3=11/168cm3
Numbers of spherical marbles, n = 9317 × (11/168) =142296
Q.9. A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively is melted and recast into the form a cone of base diameter 8cm. The height of the cone is
(a) 12cm
(b) 14cm
(c) 15cm
(d) 18cm
Correct Answer is Option (b)
Volume of spherical shell = Volume of cone recast by melting
For Spherical Shell,
Internal diameter, d1 = 4 cm
Internal radius, r1 = 2 cm[ as radius = 1/2 diameter]
External diameter, d2 = 8 cm
External radius, r2 = 4 cm
Now,
As volume of spherical shell= 4/3 π (r23 – r13)
where r1 and r2 are internal and external radii respectively.
volume of given shell = 4/3 π (43 – 23)
= 4/3 π (56)
= (224/3) π
We know that,
Volume of cone = 224π /3 cm3
For cone,
Base diameter = 8 cm
Base radius, r = 4 cm
Let Height of cone = ‘h’.
We know,Volume of cone = (1/3) π r2h,
Where r = Base radius and h = height of cone
Volume of given cone = (1/3) π42h
⇒ 224π /3 = 16πh /3
⇒ 16h = 224
h = 14 cm
So, Height of cone is 14 cm.
Q.10. A solid piece of iron in the form of a cuboid of dimensions 49cm × 33cm × 24cm, is moulded to form a solid sphere. The radius of the sphere is
(a) 21cm
(b) 23cm
(c) 25cm
(d) 19cm
Correct Answer is Option (a)
As we know,
Volume of cuboid = lbh
Where, l = length, b = breadth and h = height
For given cuboid,
Length, l = 49 cm
Breadth, b = 33 cm
Height, h = 24 cm
Volume of cube = 49× (33) × (24) cm3
Now,
Let the radius of cube be r.
As volume of sphere = 4/3 πr3
Where r = radius of sphere
Also,
Volume of cuboid = volume of sphere molded
So,
49(33)(24) = 4/3 πr3
⇒ πr3 = 29106
⇒ r3 = 29106 × 22/7
⇒ r3 = 9261
⇒ r = ∛ 9261 cm = 21 cm
Hence, radius of sphere is 21 cm
Q.11. A mason constructs a wall of dimensions 270cm × 300cm × 350cm with the bricks each of size 22.5cm × 11.25cm × 8.75cm and it is assumed that (1/8) space is covered by the mortar. Then the number of bricks used to construct the wall is
(a) 11100
(b) 11200
(c) 11000
(d) 11300
Correct Answer is Option (b)
Volume of wall = (270)(300)(350) = 28350000cm3
Volume of brick=(22.5)(11.25)(8.75) = 2214.84375cm3
(1/8) space is covered by morter = 28350000/8 = 3543750
Surface constructed = 28350000 − 3543750 = 24806250
Number of bricks = 24806250/2214.84375 = 11200
Q.12. Twelve solid spheres of the same size are made by melting a solid metallic cylinder of base diameter 2 cm and height 16 cm. The diameter of each sphere is
(a) 4 cm
(b) 3 cm
(c) 2 cm
(d) 6 cm
Correct Answer is Option (c)
Volume of a sphere of radius 'r' = (4/3)πr3
Volume of a Cylinder of Radius "R" and height "h" = πR2h
As the diameter of the cylinder is 2 cm, its radius r = 1 cm
Now, Volume of 12 spheres = Volume of the cylinder.
12 x (4/3)πr3 = π × 12 × 16
r3 = 1
r = 1 cm
Hence, diameter of the sphere = 2 cm
Q.13. The radii of the top and bottom of a bucket of slant height 45 cm are 28 cm and 7 cm, respectively. The curved surface area of the bucket is
(a) 4950 cm2
(b) 4951 cm2
(c) 4952 cm2
(d) 4953 cm2
Correct Answer is Option (a)
Given:
Slant Height, l = 45 cm
Top radius = 28 cm
Bottom radius = 7 cm
Height = 45 cm
Curved surface area =πl(r1 + r2)
= (22/7) x 45(7+28) = 4950cm2
Q.14. A medicine-capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each of its ends. The length of entire capsule is 2 cm. The capacity of the capsule is
(a) 0.36 cm3
(b) 0.35 cm3
(c) 0.34 cm3
(d) 0.33 cm3
Correct Answer is Option (a)
Capacity of the medicine = Volume of both the hemispherical parts + Volume of cylindrical part
Volume of a hemisphere of radius 'r' = (2/3)πr3
Volume of a cylindrical = πr2 h where r is the radius of the base of the cylinder and h is the height.
The hemisphere and the cylinder will have the same radius r = 0.25cm
Since total length of the toy is 2 cm, the length of the conical part will be 2 − 0.25 − 0.25 = 1.5cm
Hence, Volume of the medicine =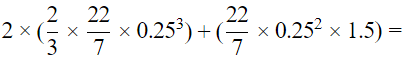
Q.15. If two solid hemispheres of same base radius r are joined together along their bases, then curved surface area of this new solid is
(a) 4 πr2
(b) 6 πr2
(c) 3 πr2
(d) 8 πr2
Correct Answer is Option (a)
We know that,
Curved surface area of a hemisphere =2πr2
So, when two solids hemispheres of same base radius are joined together along their bases, then
Curved surface area of newly formed solid sphere = 2 × 2πr2 = 4πr 2Hence, (a) is the correct option.
Q.16. A right circular cylinder of radius r cm and height h cm (h>2r) just encloses a sphere of diameter
(a) r cm
(b) 2r cm
(c) h cm
(d) 2h cm
Correct Answer is Option (b)
Sphere of diameter = diameter of base of cylinder
∴ d = 2r
Q.17. During conversion of a solid from one shape to another, the volume of the new shape will
(a) increase
(b) decrease
(c) remain unaltered
(d) be doubled
Correct Answer is Option (c)
Volume: The amount of space that a substance or object occupies, or that is enclosed within a container.
From the definition of volume ,Volume remain unchanged.
Q.18. The diameters of the two circular ends of the bucket are 44 cm and 24 cm. The height of the bucket is 35 cm. The capacity of the bucket is
(a) 32.7 litres
(b) 33.7 litres
(c) 34.7 litres
(d) 31.7 litres
Correct Answer is Option (a)
Volume of frustum of cone = (πh/3)(R2 + Rr + r2)
1 litre = 1000 cu. cm
Volume of a frustum cone =
= 32706.67 cu.cm
= 32.7 litres
Q.19. In a right circular cone, the cross-section made by a plane parallel to the base is a
(a) circle
(b) frustum of a cone
(c) sphere
(d) hemisphere
Correct Answer is Option (a)
A cone is a solid that has a circular base and a a single vertex. If the vertex is over the center of the base, it is called a right cone.
From the definition of cone, the cross-section is a circle.
Hence, option a is correct.
Q.20. Volumes of two spheres are in the ratio 64:27. The ratio of their surface areas is
(a) 3 : 4
(b) 4 : 3
(c) 9 : 16
(d) 16 : 9
Correct Answer is Option (d)
Volume of two sphere are in ratio = 64:27
We know that ,
Volume of sphere = (4/3)πr3
Then,
Then, Ratio of areas both spheres
= 16/9
Hence, this is the answer.
Exercise 12.2
Write ‘True’ or ‘False’ and justify your answer in the following:
Q.1. Two identical solid hemispheres of equal base radius r cm are stuck together along their bases. The total surface area of the combination is 6πr2.
False
When two hemispheres are joined together along their bases, a sphere of same base radius is formed.
Curved Surface Area of a sphere = 4πr2.
Q.2. A solid cylinder of radius r and height h is placed over other cylinder of same height and radius. The total surface area of the shape so formed is 4πrh + 4πr2.
False
According to the question,
When one cylinder is placed over another, the base of first cylinder and top of other cylinder will not be covered in total surface area.
We know that,
Total surface area of cylinder = 2πrh + 2πr2h, where r = base radius and h = height
Total surface area of shape formed = 2(Total surface of single cylinder) – 2(Area of base of cylinder)
= 2(2πrh + 2πr2) – 2(πr2)
= 4πrh + 2πr2
Q.3. A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. The total surface area of the combined solid is πr[√(r2 + h2 +3r + 2h].
False
When a solid cone is placed over a solid cylinder of same base radius, the base of cone and top of the cylinder will not be covered in total surface area.Since the height of cone and cylinder is same,
We get,
Total surface area of cone = πrl + πr2, where r = base radius and l = slant height
Total surface area of shape formed = Total surface area of cone + Total Surface area of cylinder – 2(Area of base)
Total surface area of cylinder = 2πrh + 2πr2h, where r = base radius and h = height
= πr(r + l) + (2πrh + 2πr2) – 2(πr2)
= πr2 + πrl + 2πrh + 2πr2 – 2πr2
= πr(r + l + h)
Q.4. A solid ball is exactly fitted inside the cubical box of side a. The volume of the ball is 4/3πa3.
False
Let the radius of sphere = r
When a solid ball is exactly fitted inside the cubical box of side a,
We get,
Diameter of ball = Edge length of cube
2r = a
Radius, r = a/2
We also know that,
Volume of sphere = 4/3πr3
Volume of ball = 4/3π(a/2)3 = 4/3π(a3/8) = 1/6πa3
Exercise 12.3
Q.1. Three metallic solid cubes whose edges are 3 cm, 4 cm and 5 cm are melted and formed into a single cube. Find the edge of the cube so formed.
We know that,
Volume of cube = a3, where a = side of cube
According to the question,
Side of first cube, a1 = 3 cm
Side of second cube, a2 = 4 cm
Side of third cube, a3 = 5 cm
Let us assume that the side of cube recast from melting these cubes = a
We know that the total volume of the 3 cubes will be the same as the volume of the newly formed cube,
Volume of new cube = (volume of 1st + 2nd + 3rd cube)
⇒ a3 = a13 + a23 + a33
⇒ a3 = (3)3 + (4)3 + (5)3
⇒ a3 = 27 + 64 + 125 = 216
⇒ a = 6 cm
Therefore, side of cube so formed is 6 cm.
Q.2. How many shots each having diameter 3 cm can be made from a cuboidal lead solid of dimensions 9cm × 11cm × 12cm?
Volume of cuboid = lbh, where, l = length, b = breadth and h = height
Cuboidal lead:
Length, l = 9 cm
Breadth, b = 11 cm
Height, h = 12 cm
Volume of lead = 9(11)(12) = 1188 cm3
Volume of sphere = 4/3πr3, where r = radius of sphere
Spherical shots,
Diameter = 3 cm
Radius, r = 1.5 cm
Volume of one shot = 4/3 × 22/7 × (1.5)3 = 99/7 cm3
Hence, the number of bullets that can be made from lead = 84.
Q.3. A bucket is in the form of a frustum of a cone and holds 28.490 litres of water. The radii of the top and bottom are 28 cm and 21 cm, respectively. Find the height of the bucket.
According to the question,
The bucket is in the form of frustum of a cone.
We know that,
Volume of frustum of a cone = 1/3 πh(r12 + r22 + r1r2), where, h = height, r1 and r2 are the radii(r1 > r2)
For bucket,
Volume of bucket = 28.490 L
1 L = 1000 cm3
Volume of bucket = 28490 cm3
Radius of top, r1 = 28 cm
Radius of bottom, r2 = 21 cm
Let the height = h.
Substituting these values in the equation to find the volume of bucket,
We have.
Volume of bucket = 1/3 πh[282 + 212 + 28(21)]
28490 = 1/3 × 22/7 × h (784 + 441 + 588) = 22/7 × h × 1813
⇒ h = (28490 × 21) / (22 × 1813)
⇒ h = 15
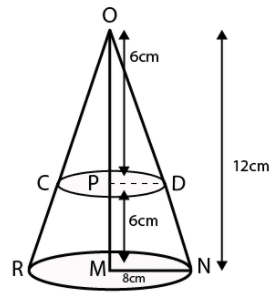
Q.4. A cone of radius 8 cm and height 12 cm is divided into two parts by a plane through the mid-point of its axis parallel to its base. Find the ratio of the volumes of two parts.
According to the question,
Height of cone = OM = 12 cm
The cone is divided from mid-point.
Hence, let the mid-point of cone = P
OP = PM = 6 cm
From △OPD and △OMN
∠POD = ∠POD [Common]
∠OPD = ∠OMN [Both 90°]
Hence, by the Angle-Angle similarity criterion
We have,
△OPD ~ △OMN
And
Similar triangles have corresponding sides in equal ratio,
So, we have,
PD/MN = OP/OMPD/8 = 6/12
PD = 4cm
[MN = 8 cm = radius of base of cone]
For First part i.e. cone
Base Radius, r = PD = 4 cm
Height, h = OP = 6 cm
We know that,
Volume of cone for radius r and height h, V = 1/3 πr2h
Volume of first part = 1/3 π(4)26 = 32π
For second part, i.e. Frustum
Bottom radius, r1 = MN = 8 cm
Top Radius, r2 = PD = 4 cm
Height, h = PM = 6 cm
We know that,
Volume of frustum of a cone = 1/3 πh(r12 + r22 + r1r2) , where, h = height, r1 and r2 are radii, (r1 > r2)
Volume of second part = 1/3 π(6)[82 + 42 + 8(4)]
= 2π(112) = 224π
Therefore, we get the ratio,
Volume of first part : Volume of second part = 32π : 224π = 1 : 7
Q.5. Two identical cubes each of volume 64 cm3 are joined together end to end. What is the surface area of the resulting cuboid?
Let the side of one cube = a
Surfaces area of resulting cuboid = 2(Total surface area of a cube) – 2(area of single surface)
We know that,
Total surface area of cube = 6a2 , where a = side of cube
⇒ Surfaces area of resulting cuboid = 2(6a2) – 2(a2) = 10a2
Also,
According to the question,
Volume of cube = 64 cm3
Volume of cube = a3
64 = a3
a = 4 cm
Therefore,
Surface area of resulting cuboid = 10a2 = 10(4)2 = 160 cm2
Q.6. From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 cm is hollowed out. Find the volume of the remaining solid.
From the figure, we get,
Volume of remaining solid = volume of cube – volume of cone
For Cube
Side, a = 7 cm
We know that,
Volume of cube = a3, where a = side of cube
Volume of cube = (7)3 = 343 cm3
For cone
Radius, r = 3 cm
Height, h = 7 cm
Volume of cone = 1/3 πr2h = 1/3 π(3)27 = 3 × (22/7) × 7 = 66 cm3
Volume of remaining solid = volume of cube – volume of cone
= 343 – 66
= 277 cm3
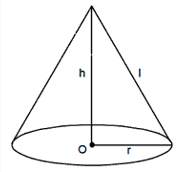
Q.7. Two cones with same base radius 8 cm and height 15 cm are joined together along their bases. Find the surface area of the shape so formed.
According to the question,
We get the figure given below,We know that,
Total surface area of shape formed = Curved area of first cone + Curved surface area of
second cone
Since, both cones are identical,
We have,
Total surface area of shape formed = Curved area of first cone + Curved surface area of
the second cone = 2(Surface area of cone)
We also know that,
Surface area of cone = πrl,
where r = radius and l = slant height
And, the total Surface area of shape so formed = 2πrl
Given in the question that,
Radius, r = 8 cm
Height, h = 15 cm
Therefore,
Area = Curved area of first cone + Curved surface area of the second cone
= 2 (Surface area of the cone)
= 2 × πrl
= 2 × π × r × √(r2 + h2)
= 2 × (22/7) × 8 × √(82 + 152)
= 50.28 × √289
= 854.85 cm2
= 855 cm2 (approx)
Hence, the surface area of shape so formed is 855cm2.
Exercise 12.4
Q.1. A solid metallic hemisphere of radius 8 cm is melted and recasted into a right circular cone of base radius 6 cm. Determine the height of the cone.
For hemisphere,
Radius, r = 8 cm
We know that,
Volume of hemisphere = 2/3 πr3, where, r = radius of hemisphere
So, we get,
Volume of given hemisphere = 2/3 × π × 83 = (1024/3) π cm3
Now,
For the cone that is recast from a hemisphere,
Base radius, r = 6 cm
We also know that,
Volume of cone = 1/3 πr2h, where, r is base radius and h is the height of the cone.
So, we get,
Volume of cone = 1/3 π(6)2h = 12πh
According to the question, we know that,
The volume remains same, when a body is reformed to another body
Volume of cylinder = Volume of cone
12πh = 1024π /3
h = 28.44 cm
Q.2. A rectangular water tank of base 11 m × 6 m contains water upto a height of 5 m. If the water in the tank is transferred to a cylindrical tank of radius 3.5 m, find the height of the water level in the tank.
Volume of water in tank = volume of cuboidal tank up to a height of 5 m
According to the question,
For cuboidal tank
Length, l = 11 m
Breadth, b = 6 m
Height, h = 5m
We know that the equation to find the volume of the tank,
Volume of tank = lbh, where, l, b and h are the length, breadth and height of tank respectively
Volume of water = 11(6)(5) = 330 m3
We also know that,
Base radius of cylindrical tank, r = 3.5 m
Let the height till which the cylindrical tank is filled = h m
Hence, using the formula,
Volume of a cylinder = πr2h, where r is base radius and h is the height of cylinder
Volume of water in cylindrical tank = π(3.5)2h
330 m3 = 22/7 × 3.5 ×3.5 × h
330 m3 = h × 38.5
h = 8.57 m
Hence, the height till which the cylindrical tank is filled = 8.57 m
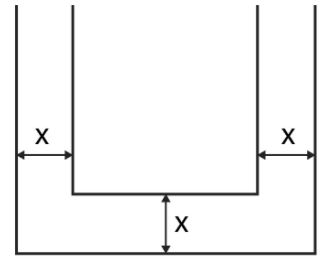
Q.3. How many cubic centimetres of iron is required to construct an open box whose external dimensions are 36 cm, 25 cm and 16.5 cm provided the thickness of the iron is 1.5 cm. If one cubic cm of iron weighs 7.5 g, find the weight of the box.
Let the length (l), breath (b), and height (h) be the external dimension of an open box and thickness be x.
The volume of metal used in box = Volume of external box – Volume of internal box
Consider external box,
Length, l = 36 cm
Breadth, b = 25 cm
Height, h = 16.5 cm
We know that the equation of the volume of cuboid is given by,
Volume of cuboid = lbh, where, l, b and h are the length, breadth and height of tank respectively
Volume of external box = 36(25)(16.5) = 14850 cm3
Since the box is open from top,
Consider internal box,
The thickness of two sides is reduced as follows,
Length, l’ = Length of external box – 2(thickness of box) = 36 – 2(1.5) = 33 cm
Breadth, b’ = Breadth of external box – 2(thickness of box) = 25 – 2(1.5) = 22 cm
Height, h’ = Height of external box – thickness of box = 16.5 – 1.5 = 15 cm
Volume of internal box = 33(22)(15) = 10890
And,
Volume of metal in box = 14850 – 10890 = 3960 cm3
We know that,
1 cm3 weighs 7.5 g
So, 3960 cm3 weighs 3960(7.5) = 29,700 g
Therefore, the weight of box is 29,700 g i.e. 29.7 kg
Q.4. The barrel of a fountain pen, cylindrical in shape, is 7 cm long and 5 mm in diameter. A full barrel of ink in the pen is used up on writing 3300 words on an average. How many words can be written in a bottle of ink containing one fifth of a litre?
Let us first calculate the volume of barrel of pen that is of cylindrical shape Consider barrel,
Since 1cm = 10 mm
Base diameter = 5 mm = 0.5 cm
Base radius, r = 0.25 cm
Height, h = 7 cm
We know that,
Volume of a cylinder = πr2h
Volume of barrel = π (0.25)27
Volume of barrel = 22/7 × 0.25 × 0.25 × 7 = 1.375 cm3
Hence, according to the question,
1.375 cm3 of ink can write 3300 words
No of words that can be written by 1 cm3 of ink = 3300/1.375 = 2400 words
1/5th of a liter = 0.2 L
We know that,
1 L = 1000 cm3
0.2 L = 200 cm3
So, no of words that can be written by 200 cm3 = 2400(200) = 480000 words
Therefore, 1/5th of a liter ink can write 480000 words.
Q.5. Water flows at the rate of 10m/minute through a cylindrical pipe 5 mm in diameter. How long would it take to fill a conical vessel whose diameter at the base is 40 cm and depth 24 cm?
Let the time taken by pipe to fill vessel = t minutes
Since water flows 10 m in 1 minute, it will flow 10t meters in t minutes.
According to the question,
Volume of conical vessel = Volume of water that passes through pipe in t minutes
Consider conical pope
Base Diameter = 40 cm
Base radius, r = 20 cm
Height, h = 24 cm
We know that the volume of cone = 1/3πr2h
Volume of conical vessel = 1/3π(20)2(24) = 3200 π cm3
Consider cylindrical pipe
Base diameter = 5 mm = 0.5 cm
Base radius, r = 0.25 cm
Water covers 10t m distance in pipe,
Hence, we get,
Height, h = 10t m = 1000t cm
We also know that,
Volume of a cylinder = πr2h
Volume of water passed in pipe = π(0.25)2(1000t) = 62.5tπ cm3
So, we have
62.5tπ = 3200
62.5t = 3200
t = 51.2 minutes
We know that,
0.2 minutes = 0.2(60) seconds = 12 seconds
Therefore, t = 51 minutes 12 seconds
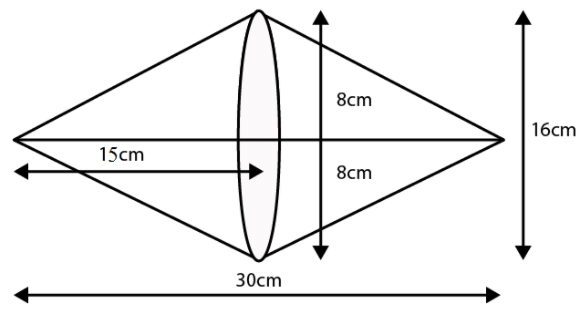
Q.6. A heap of rice is in the form of a cone of diameter 9 m and height 3.5 m. Find the volume of the rice. How much canvas cloth is required to just cover the heap?
According to the question,
Consider conical heap,
Base Diameter = 9 cm
So, base radius, r = 4.5 cm
Height, h = 3.5 cm
We know that,
Slant height,
The equation of volume of cone = 1/3πr2h
We know that,
Volume of rice = Volume of conical heap
Volume of rice = 1/3π(4.5)2(3.5)
We also know that,
Canvas requires to just cover heap = Curved surface area of conical heap
And curved surface area of a cone = πrl
Therefore, the canvas required = π(4.5)(5.7) = 80.61 cm2 [appx]
Q.7. A factory manufactures 120000 pencils daily. The pencils are cylindrical in shape each of length 25 cm and circumference of base as 1.5 cm. Determine the cost of colouring the curved surfaces of the pencils manufactured in one day at Rs 0.05 per dm2.
The shape of pencil = cylinder.
Let the radius of base = r cm
Circumference of base = 1.5 cm
Circumference of circle is 2πr = 1.5 cm
r = 1.5/2π cm
According to the question,
Height, h = 25 cm
We know that,
Curved surface area of cylinder = 2πrh
Curved surface area of pencil = 2π (1.5/2π) 25 = 37.5 cm2
1 cm = 0.1 dm
1 cm2 = 0.01 dm2
37.5 cm2 = 0.375 dm2
Cost for coloring 1 dm2 = Rs. 0.05
Cost for coloring 0.375 dm2 (i.e. 1 pencil) = Rs. 0.01875
Cost for coloring 120000 pencils = 120000 ×0.01875 = Rs. 2250
Q.8. Water is flowing at the rate of 15 km/h through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time will the level of water in pond rise by 21 cm?
Let the time taken by pipe to fill pond = t hours
Water flows 15 km in 1 hour, so, it will flow 15t meters in t hours.
We know that,
Volume of cuboidal pond up to height 21 cm = Volume of water that passes through pipe in “t” hours
Considering cuboidal pond,
Length, l = 50 m
Breadth, b = 44 m
Height, h = 21 cm = 0.21 m
We know that,
Volume of tank = lbh
Volume of water = 50(44)(0.21) = 462 m3
Considering cylindrical pipe
Base diameter = 14 cm
Base radius, r = 7 cm = 0.07 m
Height, h = 15t km = 15000t m
We also know that,
Volume of a cylinder = πr2h
Volume of water passed in pipe = π(0.07)2(15000t)
=22/7 × 0.07 × 0.07 × 15000t
= 231t cm3
So, we have
231t = 462
t = 2 hours
Time required to fill tank up to a height of 25 cm is 2 hours.
Q.9. A solid iron cuboidal block of dimensions 4.4 m × 2.6 m × 1m is recast into a hollow cylindrical pipe of internal radius 30 cm and thickness 5 cm. Find the length of the pipe.
Considering cuboidal block
Length, l = 4 m
Breadth, b = 2.6 m
Height, h = 1 m
We know that,
Volume of tank = lbh
Volume of cuboid = 4.4(2.6)(1) = 11.44 m3
We know that,
The volume remains same when a body is recast to another body.
According to the question,
Volume of cylindrical pipe = 11.44 m3
Considering pipe or the hollow cylinder
Internal radius, r2 = 30 cm = 0.3 m
Thickness = 5 cm
External radius, r1 = Internal radius + thickness = 30 + 5 = 35 cm = 0.35 m
Let the length of pipe = h
We know that,
Volume of a hollow cylinder = πh(r12 – r22)Hence,
Volume of pipe = πh((0.35)2 – (0.3)2)
So, the length of pipe is 112 m.
Q.10. 500 persons are taking a dip into a cuboidal pond which is 80 m long and 50 m broad. What is the rise of water level in the pond, if the average displacement of the water by a person is 0.04m3?
According to the question,
Average displacement by a person = 0.04 m3
Average displacement by 500 persons = 500 × 0.04 = 20 m3
Hence, the volume of water raised in pond = 20 m3
It is also given that,
Length of pond, l = 80 m
Breadth of pond, b = 50 m
Height = h
Volume of water raised in pond = 80(50)(h)
20 m3 = 4000h
h = 0.005 m = 0.5 cm
Therefore, raise in the height of water = 0.5 cm.
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Exemplar: Surface Areas & Volumes - Mathematics (Maths) Class 10
| 1. What are the formulas to find the surface area and volume of a cylinder? |  |
| 2. How do I calculate the surface area of a sphere? |  |
| 3. What is the difference between surface area and volume? |  |
| 4. How can I find the volume of a cone? |  |
| 5. Why is it important to learn about surface areas and volumes? |  |