NCERT Exemplar: Vectors | Mathematics (Maths) Class 12 - JEE PDF Download
SHORT ANSWER TYPE QUESTIONS
Q.1. Find the unit vector in the direction of sum of vectors
Ans.
Given that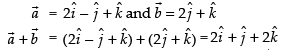
∴ Unit vector in the direction of
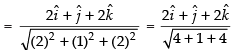
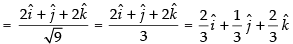
Hence, the required unit vector is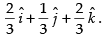
Q.2. If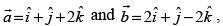 find the unit vector in the direction of
find the unit vector in the direction of
(i) 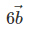
(ii)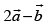
Ans.
Given that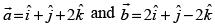
(i) 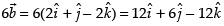
∴ Unit vector in the direction of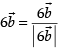
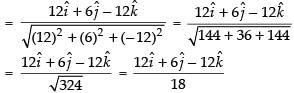

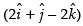
Hence, the required unit vector is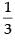

(ii)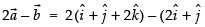 -
-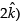

∴ Unit vector in the direction of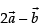
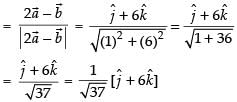
Hence, the required unit vector is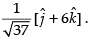
Q.3. Find a unit vector in the direction of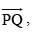 where P and Q have co-ordinates (5, 0, 8) and (3, 3, 2), respectively.
where P and Q have co-ordinates (5, 0, 8) and (3, 3, 2), respectively.
Ans.
Given coordinates are P(5, 0, 8) and Q(3, 3, 2)
∴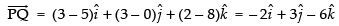
∴ Unit vector in the direction of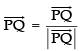
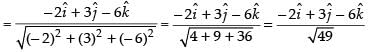
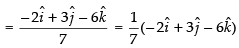
Hence, the required unit vector is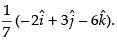
Q.4. If are the position vectors of A and B, respectively, find the position vector of a point C in BA produced such that BC = 1.5 BA.
Ans.
Given that
BC = 1.5 BA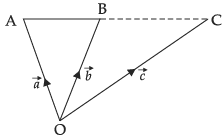 ⇒
⇒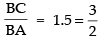
⇒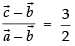
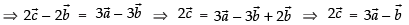
∴
Hence, the required vector is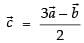
Q.5. Using vectors, find the value of k such that the points (k, – 10, 3), (1, –1, 3) and (3, 5, 3) are collinear.
Ans.
Let the given points are A( k , - 10 , 3), B(1,- 1, 3) and C(3, 5, 3)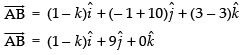
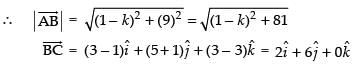
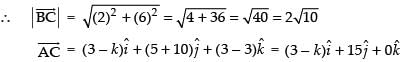

If A, B and C are collinear, then

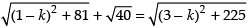
Squaring both sides, we have √
√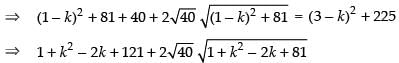
= 9 + k2- 6k + 225
⇒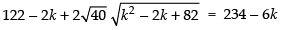
Dividing by 2, we get
⇒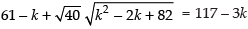
⇒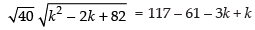
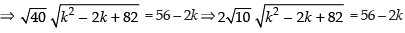
⇒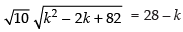 (Dividing by 2)
(Dividing by 2)
Squaring both sides, we get
⇒ 10(k2 – 2k + 82) = 784 + k2 – 56k
⇒ 10k2 – 20k + 820 = 784 + k2 – 56k
⇒ 10k2 – k2 – 20k + 56k + 820 – 784 = 0
⇒ 9k2 + 36k + 36 = 0
⇒ k2 + 4k + 4 = 0
⇒ (k + 2)2 = 0
⇒ k + 2 = 0
⇒ k = – 2
Hence, the required value is k = – 2
Q.6. A vector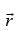 is inclined at equal angles to the three axes. If the magnitude of
is inclined at equal angles to the three axes. If the magnitude of 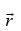 is 2 √3 units, find
is 2 √3 units, find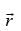
Ans.
Since, the vector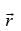 makes equal angles with the axes, their direction cosines should be same
makes equal angles with the axes, their direction cosines should be same
∴ l = m = n
We know that
l2 + m2 + n2 = 1
⇒ l2 + l2 + l2 = 1
⇒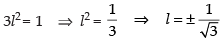
∴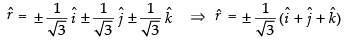
We know that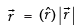
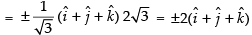
Hence, the required value of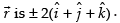
Q.7. A vector 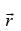 has magnitude 14 and direction ratios 2, 3, – 6. Find the direction cosines and components of
has magnitude 14 and direction ratios 2, 3, – 6. Find the direction cosines and components of 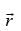 , given that
, given that 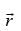 makes an acute angle with x-axis.
makes an acute angle with x-axis.
Ans.
Let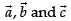 be three vectors such that
be three vectors such that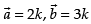 and
and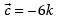
If l, m and n are the direction cosines of vector 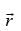 , then
, then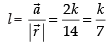
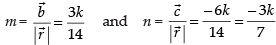
We know that l2 + m2 + n2 = 1
∴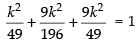
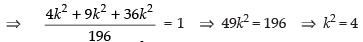
∴ k = ± 2 and l =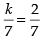
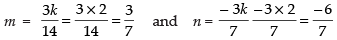
∴
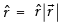
⇒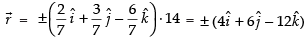
Hence, the required direction cosines are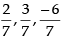 and the components of
and the components of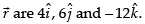
Q.8. Find a vector of magnitude 6, which is perpendicular to both the vectors 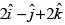 and
and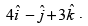
Ans.
Let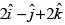 and
and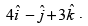
We know that unit vector perpendicular to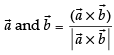

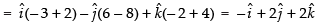
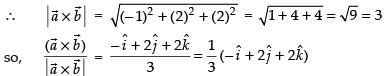
Now the vector of magnitude 6 =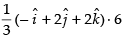

Hence, the required vector is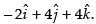
Q.9. Find the angle between the vectors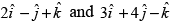 .
.
Ans.
Let and let θ be the angle between
and let θ be the angle between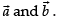
∴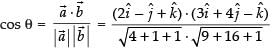
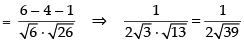
∴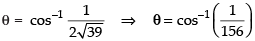
Hence, the required value of θ is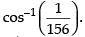
Q.10. If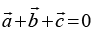 show that
show that  Interpret the result geometrically?
Interpret the result geometrically?
Ans.
Given that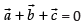
So,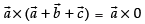
⇒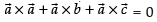
⇒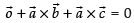
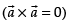
⇒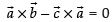
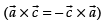
⇒ ...(i)
...(i)
Now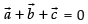
⇒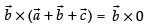
⇒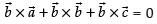
⇒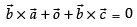
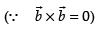
⇒
∴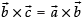 ...(ii)
...(ii)
From eq. (i) and (ii) we get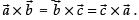
Hence proved.
Geometrical Interpretation
According to figure, we have
Area of parallelogram ABCD is
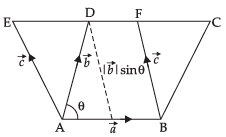
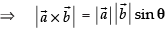
Since, the parallelograms on the same base and between the same parallel lines are equal in area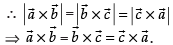
Q.11. Find the sine of the angle between the vectors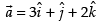 and
and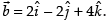
Ans.
Given that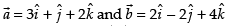
We know that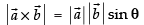
∴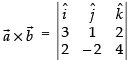
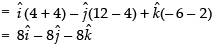
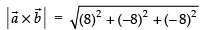
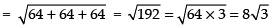
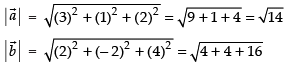
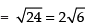
∴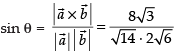
⇒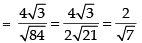
Hence,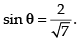
Q.12. If A, B, C, D are the points with position vectors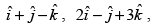
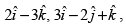 respectively, find the projection of
respectively, find the projection of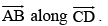
Ans.
Here, Position vector of A =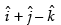
Position vector of B =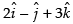
Position vector of C =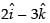
Position vector of D =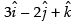
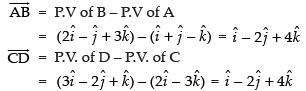
Projection of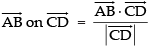
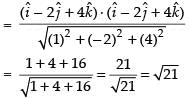
Hence, the required projection = √21 .
Q.13. Using vectors, find the area of the triangle ABC with vertices A(1, 2, 3), B(2, – 1, 4) and C(4, 5, – 1).
Ans.
Given that A(1, 2, 3), B(2, –1, 4) and C(4, 5, –1)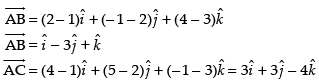
Area of ΔABC =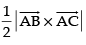 =
=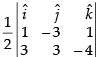
=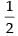
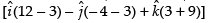
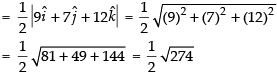
Hence, the required area is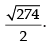
Q.14. Using vectors, prove that the parallelogram on the same base and between the same parallels are equal in area.
Ans.
Let ABCD and ABFE be two parallelograms on the same base AB and between same parallel lines AB and DF.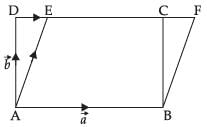 Let
Let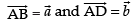
∴ Area of parallelogram ABCD =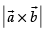
Now Area of parallelogram ABFE =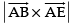
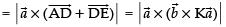
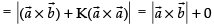
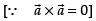
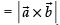
Hence proved.
LONG ANSWER TYPE QUESTIONS
Q.15. Prove that in any triangle ABC,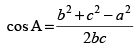 where a, b, c are the magnitudes of the sides opposite to the vertices A, B, C, respectively.
where a, b, c are the magnitudes of the sides opposite to the vertices A, B, C, respectively.
Ans.
Here, in the given figure, the components of c are c cos A and c sin A.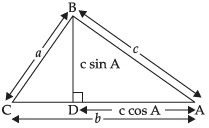 ∴
∴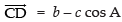
In DBDC,
a2 = CD2 + BD2
⇒ a2 = (b – c cos A)2 + (c sin A)2
⇒ a2 = b2 + c2 cos2 A – 2bc cos A + c2 sin2 A
⇒ a2 = b2 + c2(cos2 A + sin2 A) – 2bc cos A
⇒ a2 = b2 + c2 – 2bc cos A
⇒ 2bc cos A = b2 + c2 - a2
∴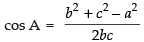
Hence Proved.
Q.16. If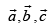 determine the vertices of a triangle, show that
determine the vertices of a triangle, show that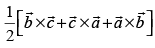 gives the vector area of the triangle. Hence deduce the condition that the three points
gives the vector area of the triangle. Hence deduce the condition that the three points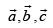 are collinear. Also find the unit vector normal to the plane of the triangle.
are collinear. Also find the unit vector normal to the plane of the triangle.
Ans.
Since,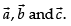 are the vertices of ΔABC
are the vertices of ΔABC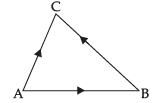
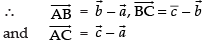
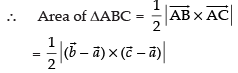
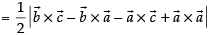
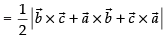
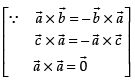
For three vectors are collinear, area of ΔABC = 0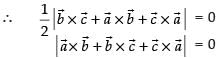
which is the condition of collinearity of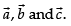
Let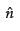 be th e unit vector normal to the plane of the ΔABC
be th e unit vector normal to the plane of the ΔABC
∴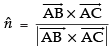
⇒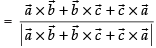
Q.17. Show that area of the parallelogram whose diagonals are given by 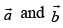 is
is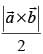 . Also find the area of the parallelogram whose diagonals are
. Also find the area of the parallelogram whose diagonals are 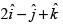 and
and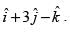
Ans.
Let ABCD be a parallelogram such that,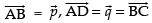
∴ by law of triangle, we get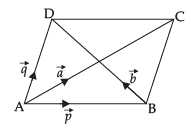
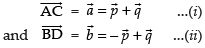
Adding eq. (i) and (ii) we get,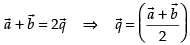
Subtracting eq. (ii) from eq. (i) we get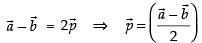
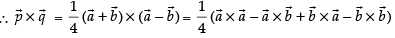
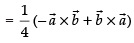
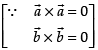
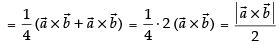
So, the area of the parallelogram ABCD =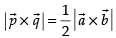
Now area of parallelogram whose diagonals are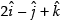 and
and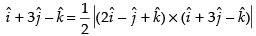

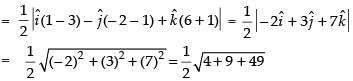

Hence, the required area is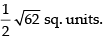
Q.18. If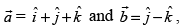 find a vector
find a vector 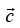 such that
such that 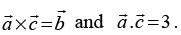
Ans.
Let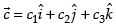
Also given that
Since,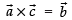
∴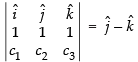
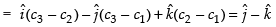
On comparing the like terms, we get
c3 – c2 = 0 ...(i)
c1 – c3 = 1 ...(ii)
and c2 – c1 = –1 ...(iii)
Now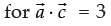
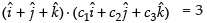
∴ c1 + c2 + c3 = 3 ...(iv)
Adding eq. (ii) and eq. (iii) we get,
c2 – c3 = 0 ...(v)
From (iv) and (v) we get
c1 + 2c2 = 3 ...(vi)
From (iii) and (vi) we get
Adding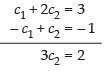
∴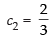
c3 – c2 = 0
⇒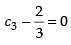
∴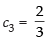
Now c2 – c1 = – 1 ⇒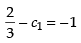
⇒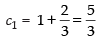
∴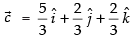
Hence,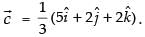
OBJECTIVE TYPE QUESTIONS
Q.19. The vector in the direction of the vector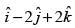 that has magnitude 9 is
that has magnitude 9 is
(a)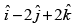
(b)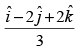
(c)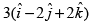
(d)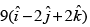
Ans. (c)
Solution.
Let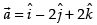
Unit vector in the direction of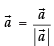
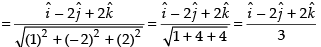
∴ Vector of magnitude 9 =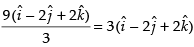
Hence, the correct option is (c).
Q.20. The position vector of the point which divides the join of points in the ratio 3 : 1 is
in the ratio 3 : 1 is
(a)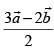
(b)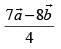
(c)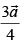
(d)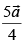
Ans. (d)
Solution.
The given vectors are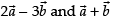 and the ratio is 3 : 1.
and the ratio is 3 : 1.
∴ The position vector of the required point c which divides the join of the given vectors 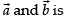

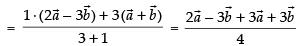
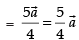
Hence, the correct option is (d).
Q.21. The vector having initial and terminal points as (2, 5, 0) and (–3, 7, 4), respectively is
(a)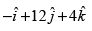
(b)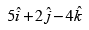
(c)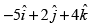
(d)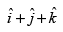
Ans. (c)
Solution.
Let A and B be two points whose coordinates are given as (2, 5, 0) and (– 3, 7, 4)
∴
⇒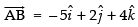
Hence, the correct option is (c).
Q.22. The angle between two vectors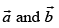 with magnitudes √3 and 4, respectively, and
with magnitudes √3 and 4, respectively, and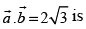
(a) π/6
(b) π/3
(c) π/2
(d) 5π/2
Ans. (b)
Solution.
Here, given that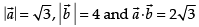
∴ From scalar product, we know that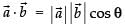
⇒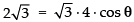
⇒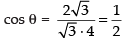
∴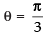
Hence, the correct option is (b).
Q.23. Find the value of λ such that the vectors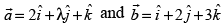
are orthogonal
(a) 0
(b) 1
(c) 3/2
(d) -5/2
Ans. (d)
Solution.
Given that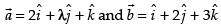
Since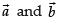 are orthogonal
are orthogonal
∴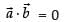
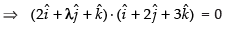
⇒ 2 + 2λ + 3 = 0
⇒ 5 + 2λ = 0 ⇒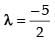
Hence, the correct option is (d).
Q.24. The value of λ for which the vectors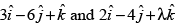
are parallel is
(a) 2/3
(b) 2/3
(c) 5/2
(d) 2/5
Ans. (a)
Solution.
Let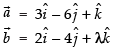
Since the given vectors are parallel,
∴ Angle between them is 0°
so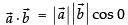
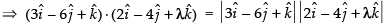
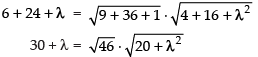
Squaring both sides, we get
900 + λ2 + 60λ = 46(20 + λ2)
⇒ 900 + λ2 + 60λ = 920 + 46λ2
⇒ λ2 – 46λ2 + 60λ + 900 – 920 = 0
⇒ - 45λ2 + 60λ - 20 = 0
⇒ 9λ2 – 12λ + 4 = 0
⇒(3λ – 2)2 = 0
⇒3λ – 2 = 0
⇒ 3λ = 2
∴ λ = 2/3
Alternate method:
Let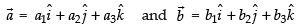
If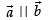
∴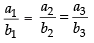
⇒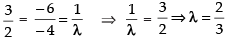
Hence, the correct option is (a).
Q.25. The vectors from origin to the points A and B are ,respectively, then the area of triangle OAB is
,respectively, then the area of triangle OAB is
(a) 340
(b) √25
(c) √229
(d)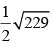
Ans. (d)
Solution.
Let O be the origin
∴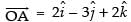
and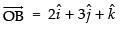
∴ Area of ΔOAB =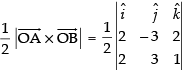
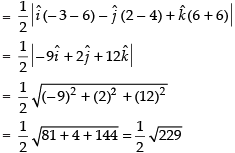
Hence the correct option is (d).
Q.26. For any vector the value of
the value of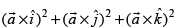 is equal to
is equal to
(a)
(b)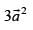
(c)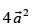
(d)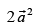
Ans. (d)
Solution.
Let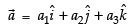
∴
Now,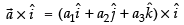
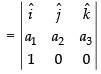
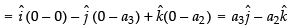
∴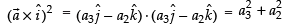
Similarly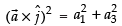
and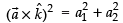
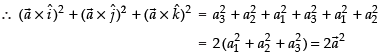
Hence, the correct option is (d).
Q.27. If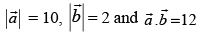 then value of
then value of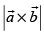 is
is
(a) 5
(b) 10
(c) 14
(d) 16
Ans. (d)
Solution.
Given that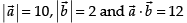
∴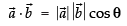
⇒ 12 = 10 × 2 × cos θ
⇒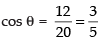
∴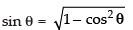
⇒
⇒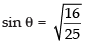
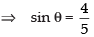
Now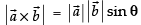
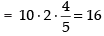
Hence, the correct option is (d).
Q.28. The vectors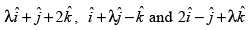 are coplanar if
are coplanar if
(a) λ = –2
(b) λ = 0
(c) λ = 1
(d) λ = – 1
Ans. (a)
Solution.
Let
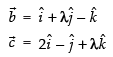
If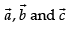 are coplanar, then
are coplanar, then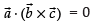
∴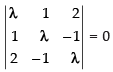
⇒ l(λ2 – 1) – 1 (λ + 2) + 2(–1 – 2l) = 0
⇒ λ3 – λ – λ – 2 – 2 – 4λ = 0
⇒ λ3 – 6λ – 4 = 0
⇒ (λ + 2) (λ2 – 2λ – 2) = 0
⇒ λ = – 2 or λ2 – 2λ – 2 = 0
⇒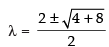
⇒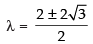
∴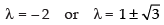
Hence, the correct option is (a).
Q.29. If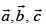 are unit vectors such that
are unit vectors such that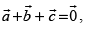 then the value of
then the value of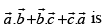
(a) 1
(b) 3
(c) -3/2
(d) None of these
Ans. (c)
Solution.
Given that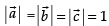
and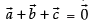
∴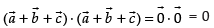
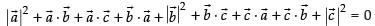
⇒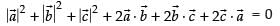
⇒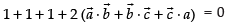
⇒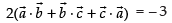
⇒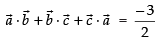
Hence, the correct option is (c).
Q.30. Projection vector of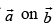 is
is
(a)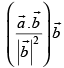
(b)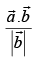
(c)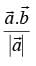
(d)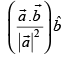
Ans. (a)
Solution.
The projection vector of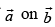
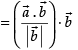
Hence, the correct option is (a).
Q.31. If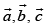 are three vectors such that
are three vectors such that
then value of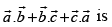
(a) 0
(b) 1
(c) – 19
(d) 38
Ans. (c)
Solution.
Given that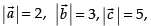
and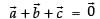
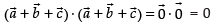
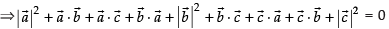
⇒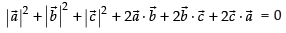
⇒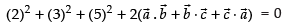
⇒
⇒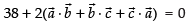
⇒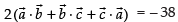
⇒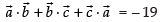
Hence, the correct option is (c).
Q.32. If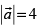 and −3 ≤ λ ≤ 2 , then the range of
and −3 ≤ λ ≤ 2 , then the range of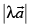 is
is
(a) [0, 8]
(b) [– 12, 8]
(c) [0, 12]
(d) [8, 12]
Ans. (b)
Solution.
Given that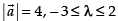
Now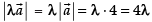
Here - 3 ≤ λ ≤ 2
⇒ - 3.4 ≤ 4λ ≤ 2.4
⇒ - 12 ≤ 4λ ≤ 8
∴ 4λ = [- 12, 8]
Hence, the correct option is (b).
Q.33. The number of vectors of unit length perpendicular to the vectors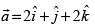 and
and
(a) one
(b) two
(c) three
(d) infinite
Ans. (b)
Solution.
The number of vectors of unit length perpendicular to vectors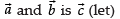
∴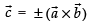
So, there will be two vectors of unit length perpendicular to vectors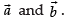
Hence, the correct option is (b).
FILL IN THE BLANKS
Q.34. The vector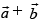 bisects the angle between the non-collinear vectors
bisects the angle between the non-collinear vectors if ________.
if ________.
Ans.
If vector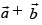 bisects the angle between non-collinear vectors
bisects the angle between non-collinear vectors
then the angle between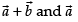 is equal to the angle between
is equal to the angle between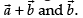
So,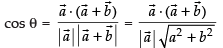 ...(i)
...(i)
Also,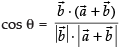 [∵ θ is same] ...(ii)
[∵ θ is same] ...(ii)
From eq. (i) and eq. (ii) we get,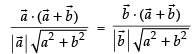
⇒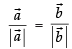
⇒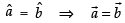
Hence, the required filler is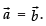
Q.35. If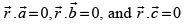 for some non-zero vector
for some non-zero vector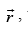 then the value of
then the value of 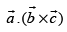 is ________
is ________
Ans.
If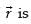 is a non-zero vector, then
is a non-zero vector, then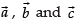 can be in the same plane.
can be in the same plane.
Since angles between 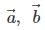 and
and 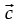 are zero i.e. θ = 0
are zero i.e. θ = 0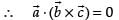
Hence the required value is 0.
Q.36. The vectors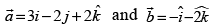 a re the adjacent sides of a parallelogram. The acute angle between its diagonals is ________.
a re the adjacent sides of a parallelogram. The acute angle between its diagonals is ________.
Ans.
Given that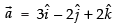
and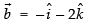
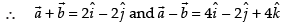
Let θ be the angle between the two diagonal vectors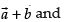

then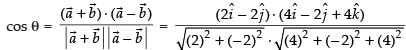
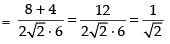
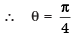
Hence the value of required filler is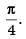
Q.37. The values of k for which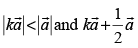 is parallel to
is parallel to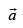 holds true are _______.
holds true are _______.
Ans.
Given that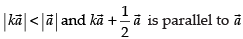
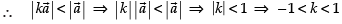
Now since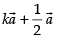 is parallel to
is parallel to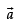
Here we see that at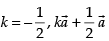 become null vector and then it will not be
become null vector and then it will not be
parallel to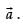
Now since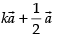 is parallel to
is parallel to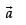
Here we see that at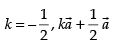 become null vector and then it will not be
become null vector and then it will not be
parallel to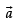
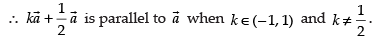
Hence, the required value of k ∈ (- 1, 1) and k ≠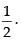
Q.38. The value of the expression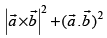 is _______.
is _______.
Ans.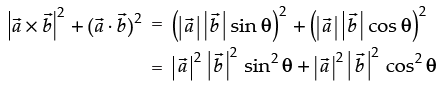
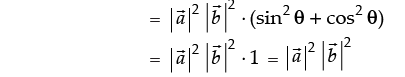
Hence, the value of the filler is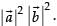
Q.39. If and
and is equal to _______.
is equal to _______.
Ans.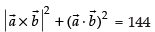
⇒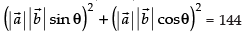
⇒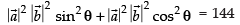
⇒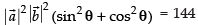
⇒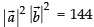
⇒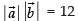
⇒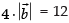
∴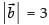
Hence, the value of the filler is 3.
Q.40. If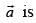 any non-zero vector, then
any non-zero vector, then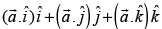
equals _______.
Ans.
Let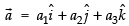
∴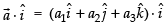
= a1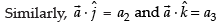
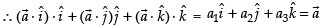
Hence, the value of the filler is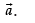
State True or False in each of the following Exercises.
Q.41. If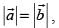 then necessarily it implies
then necessarily it implies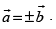
Ans.
If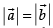 then
then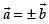 which is true.
which is true.
Hence, the statement is True.
Q.42. Position vector of a point P is a vector whose initial point is origin.
Ans.
True
Q.43. If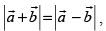 then the vectors
then the vectors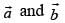 are orthogonal.
are orthogonal.
Ans.
Given that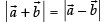
Squaring both sides, we get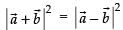
⇒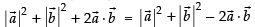
⇒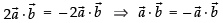
⇒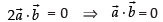
which implies that are orthogonal.
are orthogonal.
Hence the given statement is True.
Q.44. The formula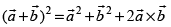 is valid for non-zero vectors
is valid for non-zero vectors
Ans.
Hence, the given statement is False.
Q.45. If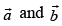 are adjacent sides of a rhombus, then
are adjacent sides of a rhombus, then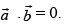
Ans.
If
So the angle between the adjacent sides of the rhombus should be 90° which is not possible.
Hence, the given statement is False.
|
203 videos|307 docs|139 tests
|
FAQs on NCERT Exemplar: Vectors - Mathematics (Maths) Class 12 - JEE
| 1. What is a vector? |  |
| 2. How is the magnitude of a vector calculated? |  |
| 3. What is the difference between a scalar and a vector quantity? |  |
| 4. How are vectors represented mathematically? |  |
| 5. What is the dot product of two vectors? |  |





















